Support Vector Classifier
A support vector classifier is a type of machine learning model that can be used for classification tasks. Given a set of training examples, each labeled as belonging to one of two classes, the goal of the support vector classifier is to find a decision boundary that maximally separates the two classes.
Mathematically, we can represent the decision boundary as a linear function of the form `w^Tx + b = 0`, where w is a vector of weights, x is a vector of features, and b is a bias term. The decision boundary is the set of points that satisfy this equation. To find the decision boundary that maximally separates the two classes, we can solve the following optimization problem:
$$\min_{w, b} \frac{1}{2} |w|^2 + C \sum_{i=1}^n \max \left(0, 1 - y_i (w^T x_i + b) \right)$$
where C is a regularization parameter that controls the trade-off between maximizing the margin and minimizing the error, yi is the label of the ith training example (either 1 or -1), and xi is the corresponding feature vector. This optimization problem can be solved using quadratic programming.
Once the optimization problem has been solved and the decision boundary has been found, we can use it to make predictions on new data points. Given a new feature vector x, we can predict the class of the corresponding example by computing the value of the linear function `w^Tx + b` and comparing it to 0. If the value is positive, we predict that the example belongs to one class; if it is negative, we predict that the example belongs to the other class.
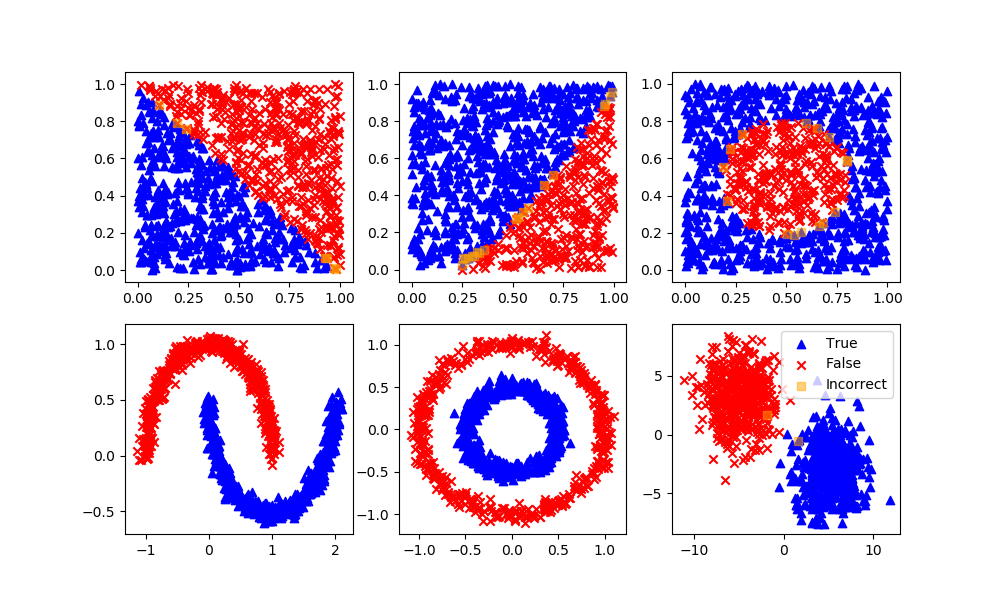
Support vector machine is a representation of the training data as points in space separated into categories by a clear gap that is as wide as possible. New examples are then mapped into that same space and predicted to belong to a category based on which side of the gap they fall. Use the Support Vector Machine (SVM) Explorer Dashboard to gain an intuitive understanding of classification and the parameters that influence the result.
Advantages: Effective in high dimensional spaces and strong ability to create complex decision boundaries.
Disadvantages: SVC does not directly provide probability estimates and is sensitive to noise, making it prone to overfitting. It has high computational complexity `O(n^2)` to `O(n^3)` for training, with limited scalability to large datasets.
SVC in Python
svm = SVC(gamma='scale', C=1.0, random_state=101)
svm.fit(XA,yA)
yP = svm.predict(XB)
Optical Character Recognition with SVC

Optical character recognition (OCR) is a method used to convert images of text into machine-readable text. It is typically used to process scanned documents and recognize the text in the images. Support vector machines (SVMs) are a type of machine learning model that can be used for classification tasks. In the context of OCR, an SVM could be trained to recognize characters in images of text.
Here is an example of using an SVM for OCR in Python:
from sklearn.datasets import load_digits
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
# Load the dataset of images of handwritten digits
digits = load_digits()
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target, random_state=0)
# Create an SVM classifier
clf = SVC(gamma=0.001)
# Train the model using the training set
clf.fit(X_train, y_train)
# Evaluate the model's performance on the test set
accuracy = clf.score(X_test, y_test)
print("Accuracy: %0.2f" % accuracy)
In this example, we use the scikit-learn library to load the dataset of images of handwritten digits, split the dataset into training and testing sets, and train an SVM classifier. We then evaluate the model's performance on the test set by computing the accuracy, which is the proportion of test images that the model correctly identifies.
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
import numpy as np
from sklearn import svm
classifier = svm.SVC(gamma=0.001)
# The digits dataset
digits = datasets.load_digits()
n_samples = len(digits.images)
data = digits.images.reshape((n_samples, -1))
# Split into train and test subsets (50% each)
X_train, X_test, y_train, y_test = train_test_split(
data, digits.target, test_size=0.5, shuffle=False)
# Learn the digits on the first half of the digits
classifier.fit(X_train, y_train)
# Test on second half of data
n = np.random.randint(int(n_samples/2),n_samples)
print('Predicted: ' + str(classifier.predict(digits.data[n:n+1])[0]))
# Show number
plt.imshow(digits.images[n], cmap=plt.cm.gray_r, interpolation='nearest')
plt.show()
MATLAB Live Script
✅ Knowledge Check
1. Which of the following statements is true about Support Vector Classifier (SVC)?
- Incorrect. SVC finds a decision boundary that maximally separates the two classes, not minimally.
- Incorrect. SVC uses a subset of training points in the decision function, making it memory efficient.
- Correct. The decision boundary can indeed be represented as a linear function of the form `w^T x + b = 0`. A non-linear SVC uses a kernel function. The kernel function transforms data to a feature space where the data becomes linearly separable.
- Incorrect. The SVC algorithm does not directly provide probability estimates. These estimates are calculated using a computationally expensive five-fold cross-validation.
2. Which of the following is NOT an advantage of Support Vector Classifier?
- Incorrect. This is actually an advantage of SVC; it can work effectively in high-dimensional spaces.
- Incorrect. This is another advantage of SVC, as it does not require all training points for the decision function.
- Correct. SVC does not directly provide probability estimates. These estimates are calculated using a computationally expensive five-fold cross-validation.
- Incorrect. SVC can indeed be effectively used for tasks like OCR, as shown in the provided Python example.
See also Support Vector Regressor
Return to Classification Overview