K-Means Clustering

K-means clustering is a type of unsupervised machine learning algorithm that is used to identify clusters within a dataset. The goal of K-means clustering is to divide the data into a specified number of clusters (K) in a way that minimizes the variance within each cluster.

The algorithm works by first initializing K centroids, which are randomly selected points within the data. The data points are then assigned to their closest centroid, and the centroids are updated to the mean of the points assigned to them. This process is repeated until the centroids no longer move or the maximum number of iterations is reached.

Mathematically, the K-means clustering algorithm can be described as follows. Let `x_1, x_2,\ldots, x_n` be the data points, where `x_i \in \mathbb{R}^d` is a d-dimensional vector. Let `c_1, c_2,\ldots, c_k` be the centroids, where `c_j \in \mathbb{R}^d` is also a d-dimensional vector. The K-means algorithm works by iteratively updating the centroids and assigning each data point to its closest centroid.

The assignment step is defined as follows:

$$y_i = \arg \min_{j \in {1, 2, ..., k}} ||x_i - c_j||^2$$

This step assigns each data point xi to the cluster whose centroid is closest to it, as measured by the Euclidean distance.

The update step is defined as follows:

$$c_j = \frac{1}{|S_j|} \sum_{i \in S_j} x_i$$

This step updates the centroid of each cluster to be the mean of the data points assigned to it. Sj is the set of indices of the data points assigned to cluster j. The algorithm terminates when the centroids no longer move or when the maximum number of iterations is reached.

The main hyper-parameter is to specify how many possible clusters (or K) there are in the dataset. The algorithm then iteratively moves the K-centers and selects the datapoints that are closest to that centroid in the cluster.

Advantages: The most common and simplest clustering algorithm.

Disadvantages: Must specify the number of clusters although this can typically be determined by increasing the number of clusters until the objective function does not change significantly.

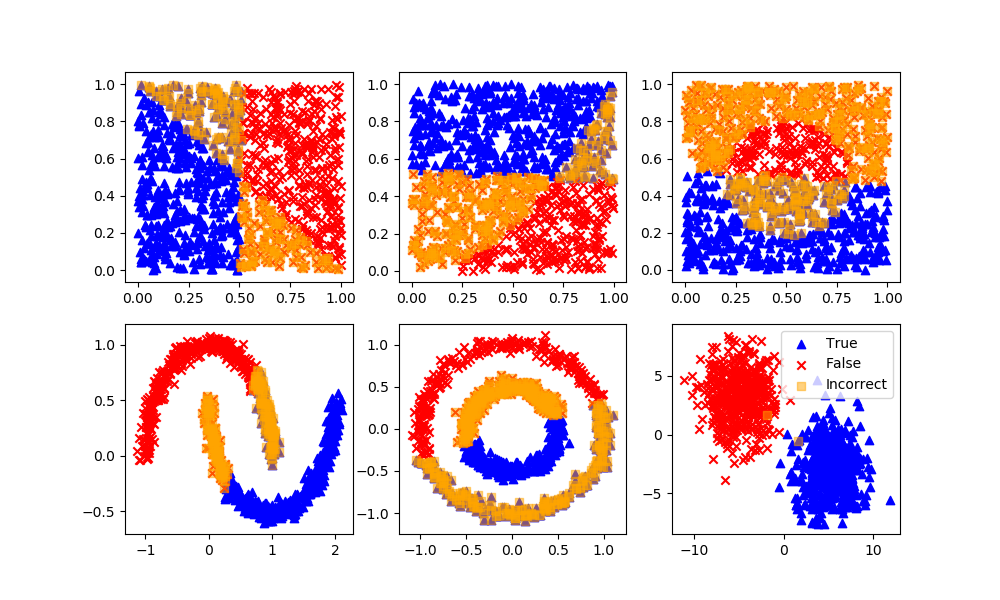
from sklearn.cluster import KMeans
km = KMeans(n_clusters=2)
km.fit(XA)
yP = km.predict(XB)
# Arbitrary labels with unsupervised clustering may need to be reversed
if len(XB[yP!=yB]) > n/4: yP = 1 - yP
[$[Get Code]]

MATLAB Live Script

KMeans MATLAB Live Script

✅ Knowledge Check

1. In the K-means clustering algorithm, how are the initial centroids determined?

A. The centroids are determined based on the mean of the entire dataset.
Incorrect. The initial centroids are randomly selected points within the data.
B. The centroids are the first K data points of the dataset.
Incorrect. The initial centroids are not necessarily the first K data points. They are randomly selected.
C. The centroids are randomly selected points within the data.
Correct. The initial centroids are indeed randomly selected from the data points.
D. The centroids are the points that are furthest apart from each other.
Incorrect. While there are various methods to initialize centroids, in the basic K-means description, they are randomly chosen.

2. How does the K-means clustering algorithm handle assigning data points to clusters?

A. It assigns each data point to the cluster based on the median distance to the centroid.
Incorrect. K-means assigns data points based on the minimum Euclidean distance, not the median distance.
B. It assigns each data point to the cluster whose centroid has the maximum Euclidean distance from the data point.
Incorrect. It assigns based on the minimum, not the maximum, Euclidean distance.
C. It assigns each data point to all the clusters simultaneously.
Incorrect. Each data point is assigned to only one cluster based on the closest centroid.
D. It assigns each data point to the cluster whose centroid is closest to it, as measured by the Euclidean distance.
Correct. Exactly. The data point is assigned to the cluster with the centroid that is the closest in terms of Euclidean distance.

Return to Classification Overview

💬