Energy Storage for Engineers
🔋 Energy Storage Balances Supply and Demand
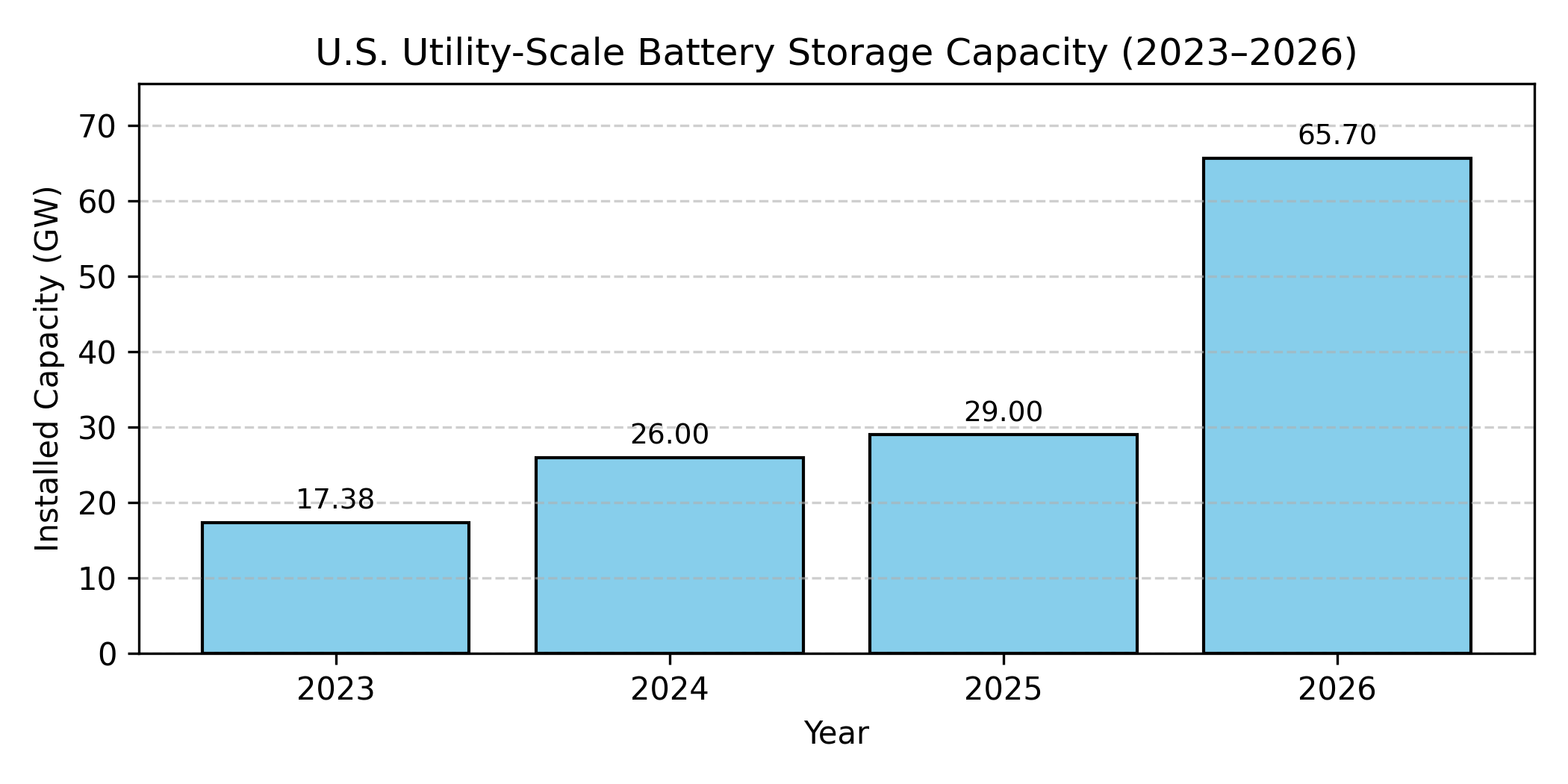
Why storage? Wind and solar generation do not always coincide with demand. As the share of renewables grows, utilities need ways to store excess energy when production is high and release it when demand peaks. The U.S. still relies heavily on pumped–storage hydropower (PSH). It accounts for ~95% of utility‑scale storage capacity. Meanwhile, battery storage is expanding rapidly. Utility‑scale battery capacity grew from 0.047 GW in 2010 to 17 GW in early 2024 and reached 29 GW by early 2025. EIA’s short‑term outlook expects capacity to double to ~65 GW by 2026. Developers plan to add more than 18 GW of battery storage in 2025, with Texas leading the boom. Mechanical storage (pumped hydro), electrochemical storage (batteries), and emerging technologies (hydrogen, supercapacitors) enable engineers to align generation with consumption.

Energy storage is also crucial for electric vehicles (EVs) and industrial applications. EVs consume roughly 34.6 kWh per 100 mi (≈ 0.346 kWh/mi). As EV adoption accelerates, charging infrastructure must rely on robust storage systems.
There are also potential benefits for locating power generation close to areas that need heat such as residential utility districts and refineries. Combined heat and power (CHP) systems (co‑generation) generate electricity while recovering waste heat. They achieve total efficiencies of 65–80%, higher than separate power and heat generation.
Fundamentals and Essential Equations
Energy storage technologies convert between forms of energy. Below are core equations that engineers use to size storage systems and evaluate their performance.
Pumped‑Hydro Storage (PHS)
Pumped‑storage hydropower uses surplus electricity to pump water uphill. Later the water is released through turbines to generate electricity. The potential energy stored in a volume of water m at height h is
$$E_\text{grav} = m g h$$
where g ≈ 9.81 m/s². In practice, energy losses from friction, evaporation, and turbine inefficiencies mean only 70–85% of the energy can be recovered. Losses can be as high as 20%, so energy returned is 0.8 × mgh.
🔢 Sample calculation: A reservoir holds 2 million m³ of water at a height difference of 100 m. The mass of water is m = ρV ≈ (1000 kg/m³)(2×10⁶ m³) = 2×10⁹ kg. E = 2×10⁹ kg × 9.81 m/s² × 100 m ≈ 1.96×10¹² J. Converting to kWh: E ≈ 1.96×10¹² J ÷ (3.6×10⁶ J/kWh) ≈ 544 MWh. If the round‑trip efficiency is 80%, the usable energy is ≈ 435 MWh.
Battery Energy Storage
Battery energy depends on cell voltage and capacity. For a single cell with capacity C_cell (Ah) and voltage U_cell,
$$E_\text{cell} = C_\text{cell} \, U_\text{cell}$$
The energy of a battery pack with N_cells cells in series/parallel is
$$E_\text{pack} = N_\text{cells} \, E_\text{cell}$$
To convert amp‑hours to watt‑hours, multiply by voltage. To convert to kilowatt‑hours (kWh), divide by 1000.
🔢 Sample calculation: An EV uses a 400 V pack built from 96 lithium‑ion cells. Each cell has 3.6 V and 3.0 Ah. Cell energy ≈ 3.0 Ah × 3.6 V = 10.8 Wh. Pack energy = 96 × 10.8 Wh ≈ 1.04 kWh. Modern EV packs typically include many more parallel cells. For example, a Tesla battery pack stores ~60-85 kWh.
Capacitors and Supercapacitors
Capacitors store electrical energy electrostatically. The energy stored in a capacitor with capacitance C and voltage V is
$$E_\text{cap} = \frac{1}{2} C V^2 = \frac{Q V}{2} = \frac{Q^2}{2C}$$
where Q is the charge. Because voltage increases as a capacitor charges, the energy is one‑half of QV. Supercapacitors (ultracapacitors) have high capacitance and power density but lower energy density than batteries, making them useful for smoothing short‑duration load variations.
🔢 Sample calculation: A supercapacitor rated C = 50 F charges to V = 12 V. E = 0.5 × 50 F × (12 V)² = 3.6 kJ (≈1.0 Wh).
Hydrogen Energy Storage
Hydrogen stores energy chemically. The lower heating value (LHV) of hydrogen is roughly 33 kWh/kg, more than 100 × the energy density of lithium‑ion batteries (~0.26 kWh/kg). However, hydrogen must be produced (often by electrolysis) and reconverted to electricity in fuel cells, with round‑trip efficiencies <40–50%. This makes hydrogen better for long‑duration storage or heavy transport.
🔢 Sample calculation: Producing 1 kg of hydrogen by electrolysis (~80% efficiency) requires ≈ 41 kWh of electricity. If this hydrogen feeds a fuel cell (~45% efficiency), the delivered electrical energy is ≈ 15 kWh. While inefficient, hydrogen enables seasonal storage.
Co‑generation (CHP) and Storage
Combined heat and power systems generate electricity and use waste heat for industrial processes or district heating. Their total efficiency is 65–80%, substantially higher than separate generation. By coupling CHP with thermal or battery storage, facilities can time‑shift electricity use, reduce fuel consumption by 20–40%, and lower emissions.
Example Problems and Case Studies
Case Study 1: Pumped Hydro vs Battery Storage
A utility compares a 600 MWh pumped‑hydro plant (round‑trip efficiency 80%) with a 600 MWh lithium‑ion battery system (round‑trip efficiency 90%). The pumped hydro stores energy by raising water 100 m. The battery stores energy chemically. Both deliver the same energy (600 MWh) when fully discharged, but the battery requires less space and offers faster response. Pumped hydro has longer life and lower cost per MWh. The choice depends on site topography and desired discharge duration.
Case Study 2: Electric Vehicle (EV) Energy Use
A typical EV consumes 0.346 kWh/mi. For a 300 mi road trip, the energy required is 0.346 kWh/mi × 300 mi ≈ 103.8 kWh. With a 500 kg lithium‑ion battery (energy density ~0.26 kWh/kg), the EV must carry roughly 130 kg of battery modules. Charging at home at $0.13/kWh costs ≈ $13.5 for the trip. By contrast, storing the same energy in hydrogen (33 kWh/kg LHV) requires ~3.1 kg of hydrogen, but only ~15 kWh of electricity is recovered due to round‑trip losses.
Case Study 3: Data Center with Battery Backup
Suppose a data center draws 50 MW continuously and needs 4 hours of backup power. Required energy = 50 MW × 4 h = 200 MWh. With a lithium‑ion system (90% efficiency), the plant must install ~222 MWh of battery capacity (200 / 0.9). At $200/kWh (including inverter, installation), the capital cost is ≈ $44 M. High efficiency reduces energy losses and ensures reliable bridging during outages.
Quiz: Energy Storage Fundamentals
1. Pumped‑storage hydropower provides most U.S. utility‑scale storage because…
Incorrect. Round‑trip efficiencies are 70–85%, so some energy is lost.
Correct. Water can be pumped uphill when electricity is cheap and released through turbines later.
Incorrect. Pumped hydro stores energy via mgh but requires large reservoirs. The volumetric energy density is lower than batteries.
Incorrect. A significant height difference is needed for gravitational storage.
2. A 3.7 V, 3000 mAh lithium‑ion cell stores about 11 Wh of energy. How much energy does a pack of 100 cells store?
Correct. Cell energy = 3.7 V×3 Ah = 11.1 Wh. 100 cells ≈ 1.1 kWh.
Incorrect. Multiply by the number of cells.
Incorrect. 30 kWh would require thousands of cells.
Incorrect. Check the conversion from mAh to kWh.
3. Which statement about hydrogen storage is most accurate?
Incorrect. Hydrogen’s LHV (~33 kWh/kg) is over 100 times greater than battery density.
Correct. Electrolysis plus fuel cells lead to efficiencies below 50%.
Incorrect. Hydrogen storage is currently expensive and used mainly for long‑duration or transport.
Incorrect. Electrolysis uses electricity to produce hydrogen.
Exercises
Exercise 1 (15 min): Pumped Hydro Reservoir Calculation
A pumped‑hydro plant stores water in an upper reservoir at height h = 120 m. The reservoir holds 1.5 million m³ of water. The round‑trip efficiency of the plant is 75%.
Tasks:
- Compute the potential energy (in MWh) stored in the reservoir.
- Compute the usable energy after accounting for efficiency.
- If the plant discharges at 200 MW, how many hours of generation can it provide?
Solution
1) Mass of water m = ρV ≈ (1000 kg/m³)(1.5×10⁶ m³) = 1.5×10⁹ kg.
Potential energy: $$E = m g h = 1.5×10^9 × 9.81 × 120 \approx 1.766×10^{12}\text{J}$$.
Convert to MWh: `E = 1.766×10^{12} J ÷ (3.6×10^{6}) ≈ 490 MWh`.
2) Usable energy with 75% efficiency: 0.75 × 490 MWh = 367.5 MWh.
3) At 200 MW, available hours = energy ÷ power = 367.5 MWh ÷ 200 MW = 1.84 h. So the plant supplies ≈ 110 minutes at 200 MW.
Exercise 2 (20 min): Battery Pack and EV Range
An electric delivery van has a battery pack consisting of 4000 cells connected in series–parallel. Each cell is rated at 3.7 V, 2500 mAh (2.5 Ah). The van consumes 0.58 kWh per mile.
Tasks:
- Determine the pack energy in kilowatt‑hours.
- Estimate the van’s range (miles) if the full pack is usable (assume 90% depth of discharge).
- If the electricity price is $0.12/kWh, compute the cost to drive 200 miles.
Solution
1) Cell energy: E_cell = 3.7 V × 2.5 Ah = 9.25 Wh. For 10,000 cells (assume all contribute), the total pack energy = 10,000 × 9.25 Wh = 92,500 Wh = 92.5 kWh.
2) Usable energy (90% depth of discharge) = 0.90 × 92.5 kWh ≈ 83.3 kWh.
Range = usable energy ÷ consumption = 83.3 kWh ÷ 0.58 kWh/mi ≈ 143.6 mi. This shows that 10,000 small cells would power a medium‑range delivery vehicle.
3) Energy required for 200 mi = 0.58 kWh/mi × 200 mi = 116 kWh. Cost = 116 kWh × $0.12/kWh = $13.92.
Exercise 3 (20 min): Hydrogen Storage for Grid Back‑Up
A data center needs 72 MWh of back‑up energy for one day. Engineers consider an electrolyzer/fuel‑cell system with hydrogen storage. Electrolysis efficiency is 80% and the fuel cell efficiency is 45%. The LHV of hydrogen is 33 kWh/kg.
Tasks:
- Compute the amount of usable electrical energy per kg of hydrogen after accounting for fuel cell efficiency.
- Determine how many kilograms of hydrogen must be stored to deliver 72 MWh.
- Calculate the electricity required to produce that hydrogen.
- Comment on advantages and disadvantages compared to battery storage.
Solution
1) Delivered energy per kg = 33 kWh/kg × 0.45 = 14.85 kWh/kg.
2) Hydrogen needed = 72,000 kWh ÷ 14.85 kWh/kg ≈ 4,848 kg.
3) Electricity to produce the hydrogen: production energy = (hydrogen LHV / electrolysis efficiency). Energy required per kg = 33 kWh ÷ 0.80 = 41.25 kWh. Total electricity = 4,848 kg × 41.25 kWh/kg ≈ 200,000 kWh (200 MWh). Round‑trip efficiency = 72 MWh ÷ 200 MWh = 36%.
4) Discussion: Hydrogen storage enables large energy reserves and long‑duration storage. However, its round‑trip efficiency (~36%) is much lower than lithium‑ion batteries (~90%). Hydrogen systems are better for seasonal or remote applications where batteries would be too expensive or heavy.
