Biomechanic Regression
Biomechanics is the study of the mechanical principles that govern human movement, such as the forces and motions involved in walking, running, jumping, and other physical activities. It is an interdisciplinary field that combines principles from physics, engineering, and anatomy to understand how the body moves and functions. Biomechanics is used in many areas, including sports science, rehabilitation, ergonomics, and robotics.
An application of biomechanics is predicting the peak force of a runner's stride. Features such as angles, hip flexion, leg lift, and speed determine the maximum force that a runner's body generates during a stride. This information is useful for coaches and athletes who want to optimize training and performance by identifying areas of weakness and improving biomechanics. By analyzing the biomechanics of a runner's stride, a coach can identify areas of inefficiency or improper technique that may increase the risk of injury. With this information, the coach can work with the athlete to modify their running technique or develop strength training exercises to improve weak areas.
Objective: Predict peak force (lpeakforce) of a runner's stride using the 10 features in the data file that are collected from several runners at various speeds. See the Running Mechanics website for more description of the data.
Features (Inputs)
- lgt = left leg ground contact time
- sr = stride rate
- sl = stride length
- lkneeswing – left knee angle during the swing phase (maximum flexion during time off ground)
- lhipflex – left hip maximum flexion
- lhipext – left hip maximum hyperextension
- lcmvert – vertical oscillation of the center of mass when coming off the left foot
- lkneesep – horizontal forward displacement between knees when leaving the ground on the left foot
- lcmtoe – horizontal forward displacement between center of mass and left toe as it touches the ground
Target (Output)
- lpeakforce - left leg peak force
The process for data regression includes importing and cleaning data, scaling the data, splitting it into train and test sets, selecting important features, and evaluating the accuracy of the model using a suitable metric. See Machine Learning for Engineers for an overview of how to process data for classification and regression.
Data and Package Import
Import the data with pandas as a DataFrame. Use pip install lazypredict to install a package that evaluates all regressors in scikit-learn.
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression
from lazypredict.Supervised import LazyRegressor
url = 'http://apmonitor.com/dde/uploads/Main/biomechanics.txt'
data = pd.read_csv(url)
data.head()
Data Cleansing
Data cleansing identifies and corrects errors in the data, such as missing values, duplicates, and outliers. This step is crucial for ensuring that the data is accurate and reliable.
data.dropna(inplace=True)
# lgt > 0
data = data[data['lgt']>0]
# 0 < left knee swing < 150
data = data[(data['lkneeswing']>0)&(data['lkneeswing']<150)]
# create boxplot to identify any other outliers
data.plot(kind='box',subplots=True,layout=(3,4))
plt.savefig('boxplot.png',dpi=300)
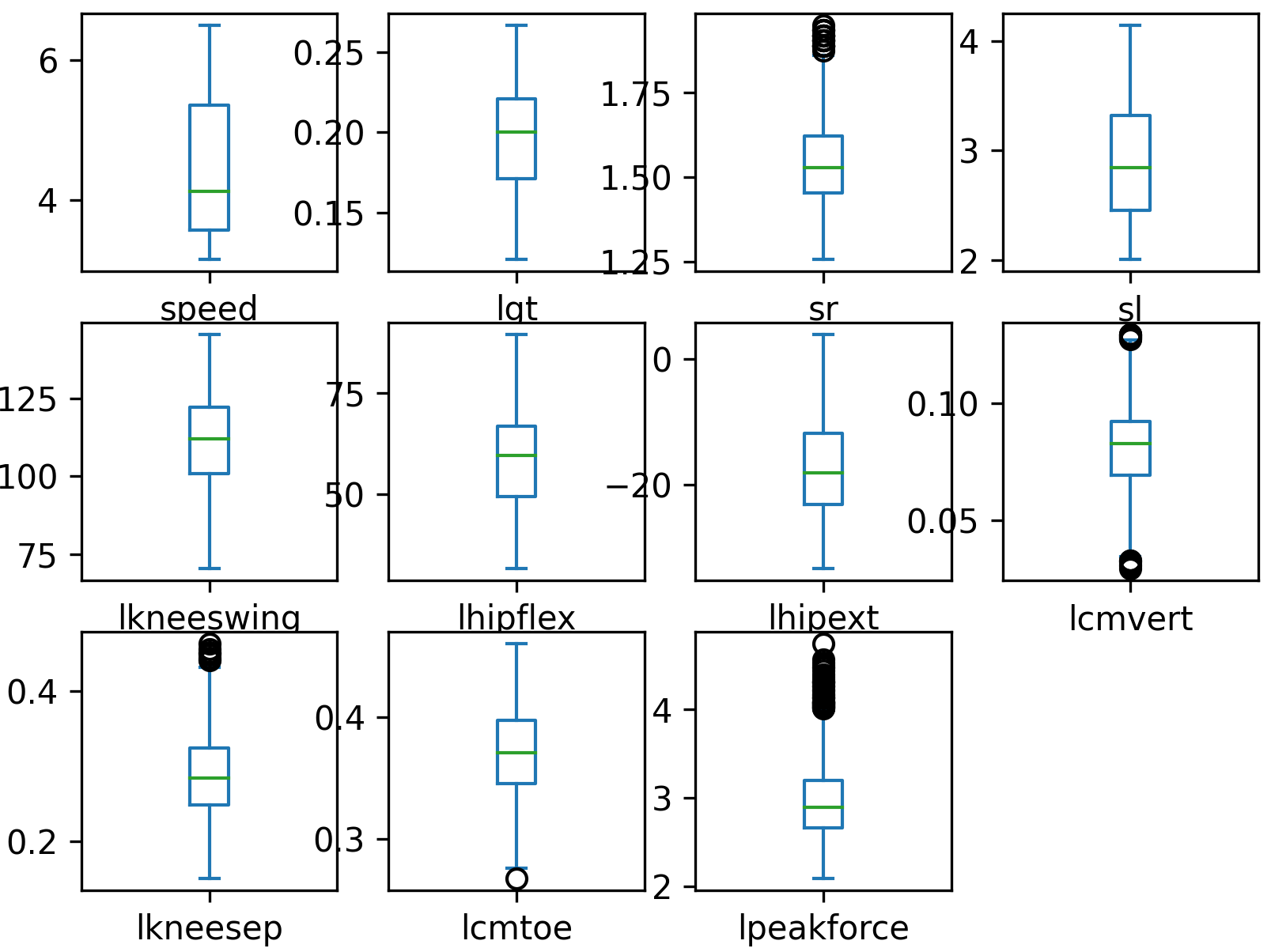
Scale and Shuffle Data
Scaling the data ensures that all the features are in the same range and improves certain regressors such as Neural Networks. This step is important for preventing bias in the model and improving accuracy. Shuffling ensures that data order is randomized.
data = data.sample(frac=1).reset_index(drop=True)
# standard scaler: mean=0, standard deviation=1
s = StandardScaler()
s_data = s.fit_transform(data)
Split Data into Train and Test Sets
Data is split into two sets: the training set and the testing set. The training set is used to train the model, while the testing set is used to evaluate accuracy.
X = s_data[:,0:-1]; y = s_data[:,-1]
# 80% for training, 20% for testing
split = int(X.shape[0] * 0.8)
X_train, y_train = X[:split], y[:split]
X_test, y_test = X[split:], y[split:]
Feature Ranking
Feature ranking selects the most important features that are highly correlated to the predicted variable. This step helps to reduce the complexity of the model and improve accuracy by keeping only the most important features.
fs = SelectKBest(score_func=f_regression, k='all')
# learn relationship from training data
fs.fit(X_train, y_train)
# scores for the features
cn = data.columns
for i in range(len(fs.scores_)):
print('Feature %s: %f' % (cn[i], fs.scores_[i]))
plt.figure()
plt.bar([i for i in range(len(fs.scores_))], fs.scores_)
ax = plt.gca()
idx = np.arange(0,X.shape[1])
ax.set_xticks(idx)
ax.set_xticklabels(cn[0:-1], rotation=25)
plt.savefig('best_features.png',dpi=300)
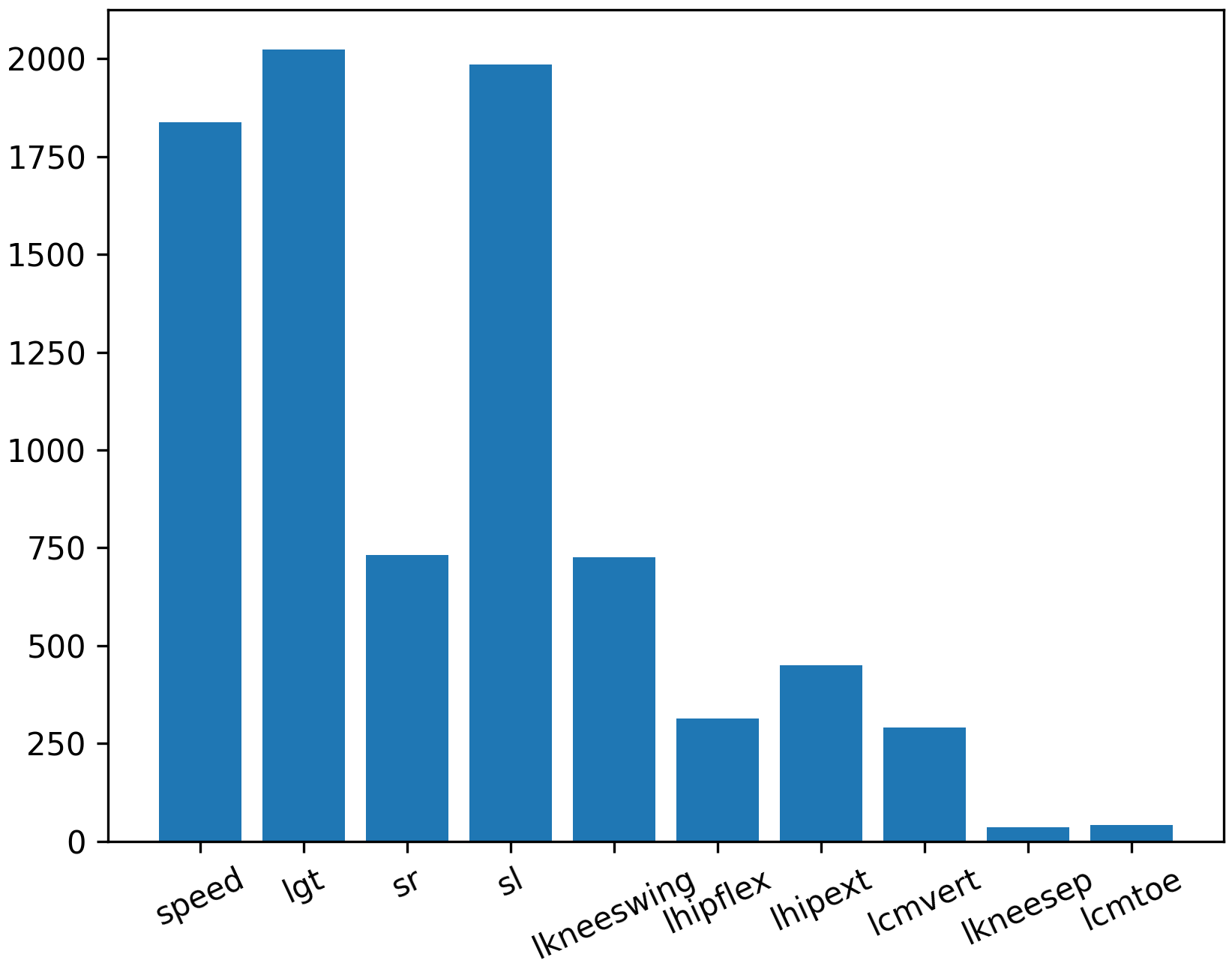
Quantify Accuracy
Use all regressors in the scikit-learn package. The accuracy of the model is evaluated using a suitable metric, such as the mean squared error (MSE) or R-squared. The scikit-learn package provides several regressors that can be used for data regression, including linear regression, decision trees, and support vector regressors.
reg = LazyRegressor(verbose=0, ignore_warnings=False, custom_metric=None)
models, predictions = reg.fit(X_train, X_test, y_train, y_test)
models.to_csv('reg_train.csv')
print(models)
| Model | Adjusted R-Squared | R-Squared | RMSE | Time Taken |
|---|---|---|---|---|
| ExtraTreesRegressor | 0.94 | 0.94 | 0.24 | 0.57 |
| KNeighborsRegressor | 0.92 | 0.93 | 0.27 | 0.01 |
| RandomForestRegressor | 0.92 | 0.93 | 0.27 | 1.65 |
| HistGradientBoostingRegressor | 0.92 | 0.92 | 0.28 | 0.59 |
| LGBMRegressor | 0.92 | 0.92 | 0.29 | 0.08 |
| BaggingRegressor | 0.91 | 0.92 | 0.29 | 0.17 |
| XGBRegressor | 0.91 | 0.91 | 0.3 | 0.14 |
| MLPRegressor | 0.9 | 0.9 | 0.31 | 1.46 |
| SVR | 0.89 | 0.89 | 0.33 | 0.19 |
| NuSVR | 0.89 | 0.89 | 0.33 | 0.23 |
| GradientBoostingRegressor | 0.86 | 0.86 | 0.37 | 0.62 |
| GaussianProcessRegressor | 0.86 | 0.86 | 0.37 | 0.29 |
| ExtraTreeRegressor | 0.84 | 0.84 | 0.39 | 0.01 |
| DecisionTreeRegressor | 0.82 | 0.82 | 0.42 | 0.02 |
| AdaBoostRegressor | 0.74 | 0.74 | 0.51 | 0.17 |
| BayesianRidge | 0.64 | 0.64 | 0.59 | 0.01 |
| ElasticNetCV | 0.64 | 0.64 | 0.59 | 0.07 |
| LassoCV | 0.64 | 0.64 | 0.59 | 0.06 |
| RidgeCV | 0.64 | 0.64 | 0.59 | 0.01 |
| Ridge | 0.64 | 0.64 | 0.59 | 0.01 |
| Lars | 0.64 | 0.64 | 0.59 | 0.01 |
| TransformedTargetRegressor | 0.64 | 0.64 | 0.59 | 0.01 |
| LarsCV | 0.64 | 0.64 | 0.59 | 0.02 |
| LassoLarsCV | 0.64 | 0.64 | 0.59 | 0.02 |
| LinearRegression | 0.64 | 0.64 | 0.59 | 0.01 |
| LassoLarsIC | 0.64 | 0.64 | 0.59 | 0.01 |
| KernelRidge | 0.64 | 0.64 | 0.59 | 0.14 |
| SGDRegressor | 0.63 | 0.64 | 0.6 | 0.01 |
| HuberRegressor | 0.6 | 0.61 | 0.62 | 0.03 |
| LinearSVR | 0.6 | 0.61 | 0.62 | 0.02 |
| OrthogonalMatchingPursuitCV | 0.6 | 0.61 | 0.62 | 0.01 |
| TweedieRegressor | 0.55 | 0.56 | 0.66 | 0.01 |
| OrthogonalMatchingPursuit | 0.5 | 0.51 | 0.7 | 0.01 |
| RANSACRegressor | 0.36 | 0.37 | 0.79 | 0.1 |
| PassiveAggressiveRegressor | 0.27 | 0.28 | 0.84 | 0.01 |
| ElasticNet | 0.21 | 0.22 | 0.88 | 0.01 |
| DummyRegressor | -0.02 | 0 | 1 | 0.01 |
| LassoLars | -0.02 | 0 | 1 | 0.01 |
| Lasso | -0.02 | 0 | 1 | 0.01 |
| QuantileRegressor | -0.03 | -0.01 | 1 | 167.62 |
Select Regressor and Evaluate Test Data
from sklearn.neighbors import KNeighborsRegressor
knn = KNeighborsRegressor(n_neighbors=5)
knn.fit(X_train,y_train)
y_pred = knn.predict(X_test)
# plot results
plt.figure()
plt.plot(y_test,y_pred,'r.')
plt.plot([-2,3],[-2,3],'k-')
plt.xlabel('measured'); plt.ylabel('predicted')
plt.grid(); plt.savefig('predict.png',dpi=300)
plt.show()
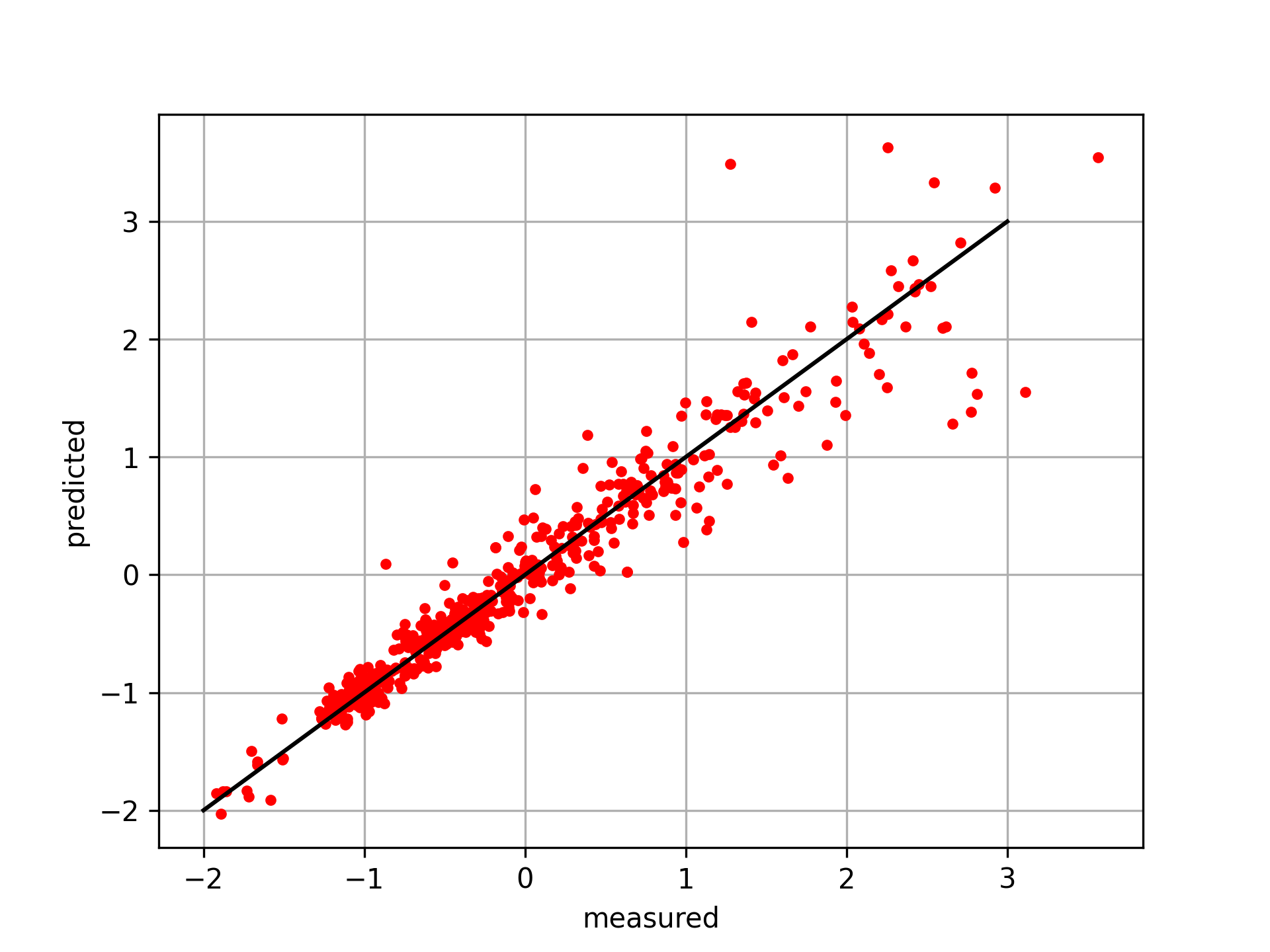
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import f_regression
from lazypredict.Supervised import LazyRegressor
url = 'http://apmonitor.com/dde/uploads/Main/biomechanics.txt'
data = pd.read_csv(url)
data.head()
# drop bad data rows
data.dropna(inplace=True)
# lgt > 0
data = data[data['lgt']>0]
# 0 < left knee swing < 150
data = data[(data['lkneeswing']>0)&(data['lkneeswing']<150)]
# create boxplot to identify any other outliers
data.plot(kind='box',subplots=True,layout=(3,4))
plt.savefig('boxplot.png',dpi=300)
# shuffle rows
data = data.sample(frac=1).reset_index(drop=True)
# standard scaler: mean=0, standard deviation=1
s = StandardScaler()
s_data = s.fit_transform(data)
# features and target
X = s_data[:,0:-1]; y = s_data[:,-1]
# 80% for training, 20% for testing
split = int(X.shape[0] * 0.8)
X_train, y_train = X[:split], y[:split]
X_test, y_test = X[split:], y[split:]
# best features
fs = SelectKBest(score_func=f_regression, k='all')
# learn relationship from training data
fs.fit(X_train, y_train)
# scores for the features
cn = data.columns
for i in range(len(fs.scores_)):
print('Feature %s: %f' % (cn[i], fs.scores_[i]))
plt.figure()
plt.bar([i for i in range(len(fs.scores_))], fs.scores_)
ax = plt.gca()
idx = np.arange(0,X.shape[1])
ax.set_xticks(idx)
ax.set_xticklabels(cn[0:-1], rotation=25)
plt.savefig('best_features.png',dpi=300)
# fit all regressors
reg = LazyRegressor(verbose=0, ignore_warnings=False, custom_metric=None)
models, predictions = reg.fit(X_train, X_test, y_train, y_test)
models.to_csv('reg_train.csv')
print(models)
# fit and test with kNN
from sklearn.neighbors import KNeighborsRegressor
knn = KNeighborsRegressor(n_neighbors=5)
knn.fit(X_train,y_train)
y_pred = knn.predict(X_test)
# plot results
plt.figure()
plt.plot(y_test,y_pred,'r.')
plt.plot([-2,3],[-2,3],'k-')
plt.xlabel('measured'); plt.ylabel('predicted')
plt.grid(); plt.savefig('predict.png',dpi=300)
plt.show()
Other Biomechanic Applications
In addition to improving performance and reducing injury risk, biomechanics can also be used to design assistive devices such as prosthetics and orthotics. By understanding the mechanical principles of human movement, engineers can design devices that mimic natural movements and provide support to individuals with physical disabilities.
Acknowledgement
Thanks to Iain Hunter of BYU Biomechanics in Exercise Science for providing the dataset.
References
- Jeong H., Park S., Estimation of the ground reaction forces from a single video camera based on the spring-like center of mass dynamics of human walking, Journal of Biomechanics, 2020 Dec Vol 2, 113, 110074. Article
- Colyer S, Needham L, Evans M, Wade L, Cosker D, Cazzola D, McGuigan P, Bilzon J. Estimation of Ground Reaction Forces from Markerless Kinematics and Comparison Against Measured Force Plate Data, ISBS Proceedings Archive, 2023, 41(1):23. Article