Hyperparameter Optimization
Hyperparameter options of classification or regression algorithms are settings not learned directly from the training data. The selection of these parameters can be determined by evaluation on a separate set of data that is reserved for optimizing the selection of hyperparameters from specified choices.
Examples of hyperparameters include the learning rate, number of hidden layers, and number of neurons in a neural network, and the regularization term in a linear classifier. The optimal values for these hyperparameters are typically determined through a process called hyperparameter optimization, which involves searching for the best combination of hyperparameter values that result in the best performance of the model on a validation dataset.
Train, Validation, Test Data
There is a validation data split for hyperparameter optimization to ensure that the model performance is evaluated in an unbiased and accurate way. The training data is used to learn the model parameters, and the validation data is used to evaluate the performance of the model and tune the hyperparameters. The test data is used as a final evaluation of the model performance, after the hyperparameters have been chosen.
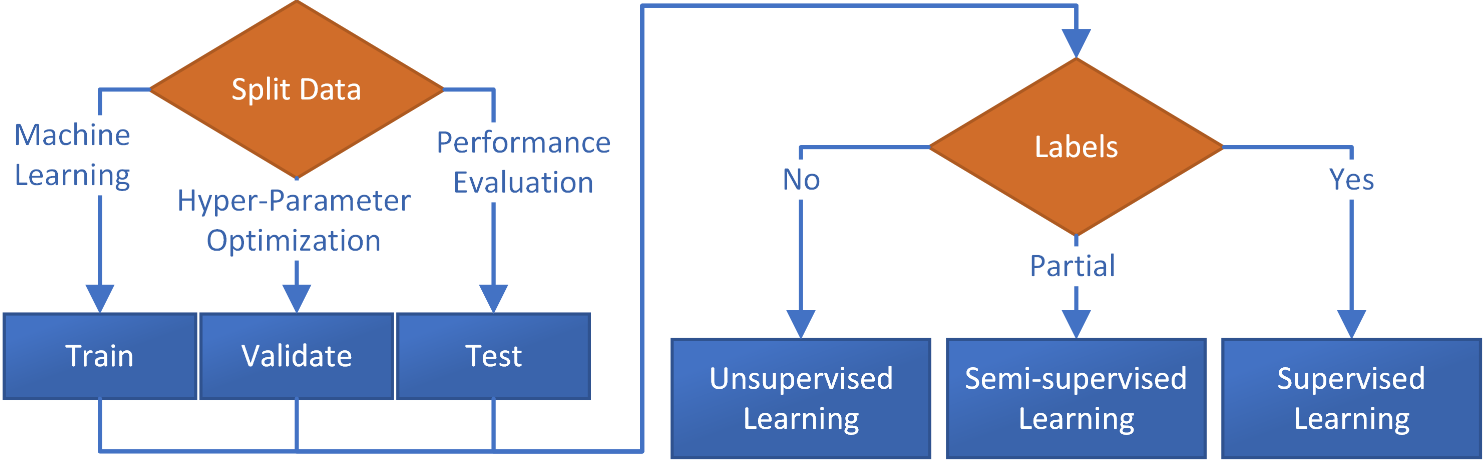
Using the same data for both training and testing the model would result in overfitting, where the model performs well on the training data but poorly on unseen data, because the model has seen the test data during the training process. By keeping the test data separate and only using it as a final evaluation, the model performance on the test data is a true representation of the performance on unseen data. Additionally, using the validation data to tune the hyperparameters and test data to evaluate the performance of the final model helps to prevent the problem of overfitting, by avoiding to use the same data for both tuning and evaluation.
Hyperparameter Search Methods
There are several common methods for hyperparameter optimization, each with its own strengths and weaknesses:
1️⃣ Grid search: A technique where a set of possible values for each hyperparameter is specified, and the algorithm will train and evaluate a model for each combination of hyperparameter values. Grid search can be computationally expensive, particularly when searching over many hyperparameters or a large range of values for each hyperparameter.
2️⃣ Random search: A technique where a random set of hyperparameter values is sampled from a predefined distribution for each hyperparameter. Random search is less computationally expensive than grid search, but still has a higher chance of finding a good set of hyperparameters than a simple grid search.
3️⃣ Bayesian optimization: A probabilistic model-based approach that uses Bayesian inference to model the function that maps the hyperparameters to the performance of the model. It uses the acquired knowledge to direct the search to the regions where it expects to find the best performance. Bayesian optimization cannot be parallelized and requires continuous hyperparameters (not categorical). It quickly converges to an optimal solution when there are few hyperparameters, but this efficiency degrades when the search dimension increases.
4️⃣ Genetic Algorithm: A evolutionary based algorithm that uses concepts of natural selection and genetics to optimize the parameters.
5️⃣ Gradient-based optimization: A method that uses gradient information to optimize the hyperparameters. This can be done using optimization algorithms such as gradient descent or Adam.
6️⃣ Hyperband: An algorithm that uses the idea of early stopping to decide when to stop training a model, which reduces the number of models that need to be trained and evaluated, making it faster than grid search or random search.
Which method to use depends on the problem, the complexity of the model, the computational resources available, and the desired trade-off between computation time and optimization quality.
Grid Search with sklearn
A grid search is a technique for hyperparameter optimization in which a set of possible values for each hyperparameter is specified, and the algorithm will train and evaluate a model for each combination of hyperparameter values. In a grid search, the user defines a grid of hyperparameters to search over, and for each combination of hyperparameter values, the algorithm trains a model using that combination, evaluate it using a metric of choice (such as accuracy or F1 score) and save the results. After training and evaluating all the models, the grid search returns the combination of hyperparameters that achieve the best performance.
For example, in the case of a KNN classifier, a grid search could be used to find the optimal number of neighbors and the optimal weighting method (uniform or distance-based) by specifying a range of values for the hyperparameter (nearest neighbors) and training a model for every combination of those values. The grid search can also use cross-validation, where the data is split into a training and validation set. So for each combination of hyperparameters, the model is trained on the training data and evaluated on the validation data. This prevents overfitting and a better estimate of the generalization performance of the model.
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV
# generate sample data with make_blobs
X, y = make_blobs(n_samples=1000, centers=5, random_state=10)
# split the data into training (60%), validation (20%), test (20%) sets
# split training (80%) and test (20%)
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.2, random_state=9)
# split off additional 20% for validation (80% * 0.25 = 20%)
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train,
test_size=0.25, random_state=7)
# define the parameter grid for the grid search
param_grid = {'n_neighbors': [3,5,7,9],
'weights': ['uniform', 'distance']}
# create a k-Nearest Neighbors classifier
knn = KNeighborsClassifier()
# create the grid search object
grid_search = GridSearchCV(knn, param_grid, cv=5)
# fit the grid search to the data
grid_search.fit(X_train, y_train)
# print the best parameters and score
print("Best parameters: ", grid_search.best_params_)
print("Best score: ", grid_search.best_score_)
# evaluate the model on the validation set
val_accuracy = grid_search.score(X_val, y_val)
print("Validation set accuracy: ", val_accuracy)
# evaluate the model on the test set
test_accuracy = grid_search.score(X_test, y_test)
print("Test set accuracy: ", test_accuracy)
Best parameters: {'n_neighbors': 7, 'weights': 'uniform'}
Best score: 0.865
Validation set accuracy: 0.84
Test set accuracy: 0.845
Grid search can be computationally expensive, particularly when searching over many hyperparameters or a large range of values for each hyperparameter.
Hyperparameter Optimization: hyperopt
hyperopt is a Python package for performing hyperparameter optimization with a variety of optimization algorithms including random search, Tree-structured Parzen Estimator (TPE), and adaptive TPE, as well as a simple and flexible way to define the search space for the hyperparameters. The main function of the package is fmin that is used to perform the optimization. The function fmin takes an objective function, the search space, the optimization algorithm, and the maximum number of evaluations as input. The objective function takes the hyperparameters as input and returns a dictionary with the loss (or negative of the performance metric) and the status of the optimization. In addition to the fmin function, hyperopt also provides a number of helper functions for defining the search space. For example, hp.quniform and hp.qloguniform for continuous variables, hp.choice for categorical variables and hp.randint for integers. hyperopt provides a built-in support for parallel execution and early stopping. It can be used in combination with most machine learning libraries, such as scikit-learn, TensorFlow, and PyTorch. It is a popular choice among data scientists and researchers for the ease of use and ability to find better solutions in a relatively small number of evaluations.
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from hyperopt import fmin, tpe, hp, STATUS_OK
# Generate data using make_blobs
X, y = make_blobs(n_samples=1000, n_features=2,
centers=5, random_state=12)
# Split data into train and test sets
X_train, X_test, y_train, y_test = \
train_test_split(X, y, test_size=0.2, random_state=42)
# Define the search space for the hyperparameters
space = {'n_neighbors': hp.quniform('n_neighbors', 2, 20, 1),
'weights': hp.choice('weights', ['uniform', 'distance'])}
def objective(params):
params['n_neighbors'] = int(params['n_neighbors'])
knn = KNeighborsClassifier(**params)
knn.fit(X_train, y_train)
y_pred = knn.predict(X_test)
acc = accuracy_score(y_test, y_pred)
return {'loss': -acc, 'status': STATUS_OK}
best = fmin(objective, space, algo=tpe.suggest, max_evals=100)
print(best)
Best Result
{'n_neighbors': 6.0, 'weights': 0}

✅ Knowledge Check
1. Which optimization method is useful when there's a need to balance between computational cost and optimization quality?
- Incorrect. While grid search is thorough, it can be computationally expensive, especially with a large number of hyperparameters.
- Correct. Random search samples hyperparameters from a distribution and might provide a good balance between computational cost and optimization quality.
- Incorrect. Gradient-based optimization is powerful but may not always be the most efficient for all types of hyperparameter spaces.
- Incorrect. Hyperband uses the idea of early stopping, which can be efficient, but its main advantage is speed, not necessarily a balance between computation time and optimization quality.
2. In the context of KNN classification, what might be the purpose of performing a grid search?
- Incorrect. KNN does not use activation functions, which are more common in neural networks.
- Incorrect. KNN doesn't have layers like neural networks.
- Incorrect. While preprocessing is crucial for KNN, grid search typically optimizes model-specific hyperparameters rather than preprocessing methods.
- Correct. In the case of a KNN classifier, a grid search can be used to find the optimal number of neighbors and the optimal weighting method.