TCLab D - Empirical Model Estimation

Main.TCLabD History

Show minor edits - Show changes to markup

February 10, 2023, at 06:10 PM by 10.35.117.248 -
Deleted line 456:
  1. use remote=True for MacOS
Restore
January 04, 2021, at 08:50 PM by 10.35.117.248 -
Added lines 684-686:

Virtual TCLab on Google Colab

Lab A | Lab B | Lab C | Lab D | Lab E | Lab F | Lab G | Lab H
Restore
January 02, 2021, at 09:41 PM by 136.36.4.38 -
Added lines 340-377:

plt.show() (:sourceend:) (:divend:)

(:toggle hide gekko_labDARX button show="Lab D: Python GEKKO 2nd Order ARX":) (:div id=gekko_labDARX:) (:source lang=python:) from gekko import GEKKO import numpy as np import pandas as pd import matplotlib.pyplot as plt

  1. load data and parse into columns

url = 'http://apmonitor.com/do/uploads/Main/tclab_dyn_data2.txt' data = pd.read_csv(url) t = data['Time'] u = data'H1','H2'? y = data'T1','T2'?

m = GEKKO()

  1. system identification

na = 2 # output coefficients nb = 2 # input coefficients yp,p,K = m.sysid(t,u,y,na,nb,pred='meas')

plt.figure() plt.subplot(2,1,1) plt.plot(t,u,label=r'$Heater_1$') plt.legend([r'$Heater_1$',r'$Heater_2$']) plt.ylabel('Heaters') plt.subplot(2,1,2) plt.plot(t,y) plt.plot(t,yp,) plt.legend([r'$T1_{meas}$',r'$T2_{meas}$', r'$T1_{pred}$',r'$T2_{pred}$']) plt.ylabel('Temperature (°C)') plt.xlabel('Time (sec)')

Restore
January 29, 2019, at 03:34 PM by 174.148.204.25 -
Added lines 352-353:

See information on Second Order Systems and Moving Horizon Estimation.

Deleted lines 354-355:

See information on Second Order Systems and Moving Horizon Estimation.

Restore
January 29, 2019, at 03:33 PM by 174.148.204.25 -
Deleted lines 12-13:
  • Solution in Python and MATLAB
Changed line 14 from:

<iframe width="560" height="315" src="https://www.youtube.com/embed/Cp6fPUptc74" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>

to:

<iframe width="560" height="315" src="https://www.youtube.com/embed/yRvffV7ZPOA" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>

Added lines 347-350:

(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/Cp6fPUptc74" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> (:htmlend:)

Restore
January 29, 2019, at 01:52 PM by 45.56.3.173 -
Deleted line 211:

(:source lang=python:)

Restore
January 28, 2019, at 03:24 PM by 174.148.229.170 -
Changed lines 591-592 from:
        plt.plot(tm[0:i],tau3s[0:i]*10,'r--',label=r'$\tau_3$ x 10')        
        plt.ylabel('Gains')
to:
        plt.plot(tm[0:i],tau3s[0:i]*10,'r--',label=r'$\tau_3$ x 10')
        plt.ylabel('Time constant')
Restore
January 28, 2019, at 03:17 PM by 174.148.229.170 -
Added lines 344-628:

(:sourceend:) (:divend:)

2nd Order System Identification with MHE

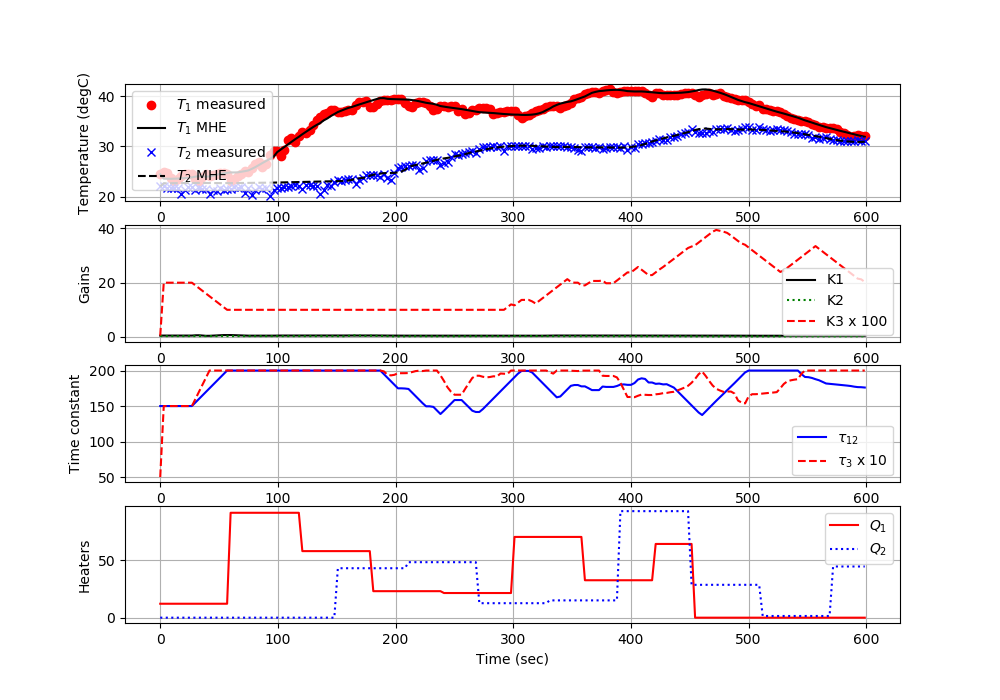
See information on Second Order Systems and Moving Horizon Estimation.

(:toggle hide gekko_labDMHE button show="Lab D: Python GEKKO 2nd Order MHE":) (:div id=gekko_labDMHE:) (:source lang=python:) import numpy as np import time import matplotlib.pyplot as plt import random

  1. get gekko package with:
  2. pip install gekko

from gekko import GEKKO

  1. get tclab package with:
  2. pip install tclab

from tclab import TCLab

  1. save txt file

def save_txt(t,Q1,Q2,T1,T2): 

    data = np.vstack((t,Q1,Q2,T1,T2))  # vertical stack
    data = data.T                 # transpose data
    top = 'Time (sec), Heater 1, Heater 2, '         + 'Temperature 1, Temperature 2' 
    np.savetxt('data.txt',data,delimiter=',',header=top,comments='')
  1. Connect to Arduino

a = TCLab()

  1. Final time

tf = 10 # min

  1. number of data points (every 3 seconds)

n = tf * 20 + 1

  1. Configure heater levels
  2. Percent Heater (0-100%)

Q1s = np.zeros(n) Q2s = np.zeros(n)

  1. Heater random steps every 50 sec
  2. Alternate steps by Q1 and Q2
  3. with rapid, random changes every 10 cycles

for i in range(n): 

    if i%20==0:
        Q1s[i:i+20] = random.random() * 100.0
    if (i+10)%20==0:
        Q2s[i:i+20] = random.random() * 100.0
  1. heater 2 initially off

Q2s[0:50] = 0.0

  1. heater 1 off at end (last 50 cycles)

Q1s[-50:-1] = 0.0

  1. Record initial temperatures (degC)

T1m = a.T1 * np.ones(n) T2m = a.T2 * np.ones(n)

  1. Store MHE values for plots

Tmhe1 = T1m[0] * np.ones(n) Tmhe2 = T2m[0] * np.ones(n) K1s = 0.5 * np.ones(n) K2s = 0.3 * np.ones(n) K3s = 0.005 * np.ones(n) tau12s = 150.0 * np.ones(n) tau3s = 5.0 * np.ones(n)

  1. Initialize Model as Estimator
  2. use remote=True for MacOS

m = GEKKO(name='tclab-mhe',remote=False)

  1. 120 second time horizon, 40 steps

m.time = np.linspace(0,120,41)

  1. Parameters to Estimate

K1 = m.FV(value=0.5) K1.STATUS = 0 K1.FSTATUS = 0 K1.DMAX = 0.1 K1.LOWER = 0.1 K1.UPPER = 1.0

K2 = m.FV(value=0.3) K2.STATUS = 0 K2.FSTATUS = 0 K2.DMAX = 0.1 K2.LOWER = 0.1 K2.UPPER = 1.0

K3 = m.FV(value=0.2) K3.STATUS = 0 K3.FSTATUS = 0 K3.DMAX = 0.01 K3.LOWER = 0.1 K3.UPPER = 1.0

tau12 = m.FV(value=150) tau12.STATUS = 0 tau12.FSTATUS = 0 tau12.DMAX = 5.0 tau12.LOWER = 50.0 tau12.UPPER = 200

tau3 = m.FV(value=15) tau3.STATUS = 0 tau3.FSTATUS = 0 tau3.DMAX = 1 tau3.LOWER = 10 tau3.UPPER = 20

  1. Measured inputs

Q1 = m.MV(value=0) Q1.FSTATUS = 1 # measured

Q2 = m.MV(value=0) Q2.FSTATUS = 1 # measured

  1. State variables

TH1 = m.SV(value=T1m[0]) TH2 = m.SV(value=T2m[0])

  1. Measurements for model alignment

TC1 = m.CV(value=T1m[0]) TC1.STATUS = 1 # minimize error TC1.FSTATUS = 1 # receive measurement TC1.MEAS_GAP = 0.1 # measurement deadband gap

TC2 = m.CV(value=T2m[0]) TC2.STATUS = 1 # minimize error TC2.FSTATUS = 1 # receive measurement TC2.MEAS_GAP = 0.1 # measurement deadband gap

Ta = m.Param(value=23.0) # degC

  1. Heat transfer between two heaters

DT = m.Intermediate(TH2-TH1)

  1. Empirical correlations

m.Equation(tau12 * TH1.dt() + (TH1-Ta) == K1*Q1 + K3*DT) m.Equation(tau12 * TH2.dt() + (TH2-Ta) == K2*Q2 - K3*DT) m.Equation(tau3 * TC1.dt() + TC1 == TH1) m.Equation(tau3 * TC2.dt() + TC2 == TH2)

  1. Global Options

m.options.IMODE = 5 # MHE m.options.EV_TYPE = 1 # Objective type m.options.NODES = 3 # Collocation nodes m.options.SOLVER = 3 # IPOPT m.options.COLDSTART = 1 # COLDSTART on first cycle

  1. Create plot

plt.figure(figsize=(10,7)) plt.ion() plt.show()

  1. Main Loop

start_time = time.time() prev_time = start_time tm = np.zeros(n)

try: 

    for i in range(1,n):
        # Sleep time
        sleep_max = 3.0
        sleep = sleep_max - (time.time() - prev_time)
        if sleep>=0.01:
            time.sleep(sleep-0.01)
        else:
            time.sleep(0.01)

        # Record time and change in time
        t = time.time()
        dt = t - prev_time
        prev_time = t
        tm[i] = t - start_time

        # Read temperatures in Celsius 
        T1m[i] = a.T1
        T2m[i] = a.T2

        # Insert measurements
        TC1.MEAS = T1m[i]
        TC2.MEAS = T2m[i]
        Q1.MEAS = Q1s[i-1]
        Q2.MEAS = Q2s[i-1]

        # Start estimating U after 10 cycles (20 sec)
        if i==10:
            K1.STATUS = 1
            K2.STATUS = 1
            K3.STATUS = 1
            tau12.STATUS = 1
            tau3.STATUS = 1

        # Predict Parameters and Temperatures with MHE
        # use remote=False for local solve
        m.solve() 

        if m.options.APPSTATUS == 1:
            # Retrieve new values
            Tmhe1[i]  = TC1.MODEL
            Tmhe2[i]  = TC2.MODEL
            K1s[i]    = K1.NEWVAL
            K2s[i]    = K2.NEWVAL
            K3s[i]    = K3.NEWVAL
            tau12s[i] = tau12.NEWVAL
            tau3s[i]  = tau3.NEWVAL
        else:
            # Solution failed, copy prior solution
            Tmhe1[i]  = Tmhe1[i-1]
            Tmhe2[i]  = Tmhe1[i-1]
            K1s[i]    = K1s[i-1]   
            K2s[i]    = K2s[i-1]   
            K3s[i]    = K3s[i-1]   
            tau12s[i] = tau12s[i-1]
            tau3s[i]  = tau3s[i-1] 

        # Write new heater values (0-100)
        a.Q1(Q1s[i])
        a.Q2(Q2s[i])

        # Plot
        plt.clf()
        ax=plt.subplot(4,1,1)
        ax.grid()
        plt.plot(tm[0:i],T1m[0:i],'ro',label=r'$T_1$ measured')
        plt.plot(tm[0:i],Tmhe1[0:i],'k-',label=r'$T_1$ MHE')
        plt.plot(tm[0:i],T2m[0:i],'bx',label=r'$T_2$ measured')
        plt.plot(tm[0:i],Tmhe2[0:i],'k--',label=r'$T_2$ MHE')
        plt.ylabel('Temperature (degC)')
        plt.legend(loc=2)
        ax=plt.subplot(4,1,2)
        ax.grid()
        plt.plot(tm[0:i],K1s[0:i],'k-',label='K1')
        plt.plot(tm[0:i],K2s[0:i],'g:',label='K2')        
        plt.plot(tm[0:i],K3s[0:i]*100,'r--',label='K3 x 100')
        plt.ylabel('Gains')
        plt.legend(loc='best')
        ax=plt.subplot(4,1,3)
        ax.grid()
        plt.plot(tm[0:i],tau12s[0:i],'b-',label=r'$\tau_{12}$')
        plt.plot(tm[0:i],tau3s[0:i]*10,'r--',label=r'$\tau_3$ x 10')        
        plt.ylabel('Gains')
        plt.legend(loc='best')
        ax=plt.subplot(4,1,4)
        ax.grid()
        plt.plot(tm[0:i],Q1s[0:i],'r-',label=r'$Q_1$')
        plt.plot(tm[0:i],Q2s[0:i],'b:',label=r'$Q_2$')
        plt.ylabel('Heaters')
        plt.xlabel('Time (sec)')
        plt.legend(loc='best')
        plt.draw()
        plt.pause(0.05)

    # Turn off heaters
    a.Q1(0)
    a.Q2(0)
    save_txt(tm,Q1s,Q2s,T1m,T2m)
    # Save figure
    plt.savefig('tclab_mhe.png')
  1. Allow user to end loop with Ctrl-C

except KeyboardInterrupt: 

    # Disconnect from Arduino
    a.Q1(0)
    a.Q2(0)
    print('Shutting down')
    a.close()
    plt.savefig('tclab_mhe.png')
  1. Make sure serial connection still closes when there's an error

except: 

    # Disconnect from Arduino
    a.Q1(0)
    a.Q2(0)
    print('Error: Shutting down')
    a.close()
    plt.savefig('tclab_mhe.png')
    raise
Restore
January 28, 2019, at 02:59 PM by 174.148.229.170 -
Added line 103:

(:source lang=python:)

Added line 226:

(:source lang=python:)

Deleted line 343:

(:source lang=python:)

Restore
January 28, 2019, at 02:58 PM by 174.148.229.170 -
Changed lines 99-100 from:

See information on .

to:

See information on First Order Systems.

Changed line 221 from:

See information on .

to:

See information on Second Order Systems.

Restore
January 28, 2019, at 02:58 PM by 174.148.229.170 -
Changed line 23 from:

(:toggle hide gekko_labEd button show="Lab D: Python TCLab Generate Step Data":)

to:

(:toggle hide gekko_labDd button show="Lab D: Python TCLab Generate Step Data":)

Restore
January 28, 2019, at 02:57 PM by 174.148.229.170 -
Added lines 1-409:

(:title TCLab D - Empirical Model Estimation:) (:keywords Arduino, Empirical, System Identification, Regression, temperature, control, process control, course:) (:description Regression of TCLab Parameters with Empirical System Identification using Arduino Data:)

The TCLab is a hands-on application of machine learning and advanced temperature control with two heaters and two temperature sensors. The labs reinforce principles of model development, estimation, and advanced control methods. This is the fourth exercise and it involves system identification using empirical data. The predictions are aligned to the measured values through an optimizer that adjusts the empirical parameters to minimize a sum of squared error or sum of absolute values objective. There are 1st order, 2nd order, and higher order estimation examples.

Lab Problem Statement

Data and Solutions

  • Solution in Python and MATLAB

(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/Cp6fPUptc74" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> (:htmlend:)

(:toggle hide gekko_labEd button show="Lab D: Python TCLab Generate Step Data":) (:div id=gekko_labDd:) (:source lang=python:) import numpy as np import pandas as pd import tclab import time import matplotlib.pyplot as plt

  1. generate step test data on Arduino

filename = 'tclab_dyn_data2.csv'

  1. heater steps

Q1d = np.zeros(601) Q1d[10:200] = 80 Q1d[200:280] = 20 Q1d[280:400] = 70 Q1d[400:] = 50

Q2d = np.zeros(601) Q2d[120:320] = 100 Q2d[320:520] = 10 Q2d[520:] = 80

  1. Connect to Arduino

a = tclab.TCLab() fid = open(filename,'w') fid.write('Time,H1,H2,T1,T2\n') fid.close()

  1. run step test (10 min)

for i in range(601): 

    # set heater values
    a.Q1(Q1d[i])
    a.Q2(Q2d[i])
    print('Time: ' + str(i) +           ' H1: ' + str(Q1d[i]) +           ' H2: ' + str(Q2d[i]) +           ' T1: ' + str(a.T1)   +           ' T2: ' + str(a.T2))
    # wait 1 second
    time.sleep(1)
    fid = open(filename,'a')
    fid.write(str(i)+',str(Q1d[i]),str(Q2d[i]),'               +str(a.T1)+',str(a.T2)\n')
  1. close connection to Arduino

a.close()

  1. read data file

data = pd.read_csv(filename)

  1. plot measurements

plt.figure() plt.subplot(2,1,1) plt.plot(data['Time'],data['H1'],'r-',label='Heater 1') plt.plot(data['Time'],data['H2'],'b--',label='Heater 2') plt.ylabel('Heater (%)') plt.legend(loc='best') plt.subplot(2,1,2) plt.plot(data['Time'],data['T1'],'r.',label='Temperature 1') plt.plot(data['Time'],data['T2'],'b.',label='Temperature 2') plt.ylabel('Temperature (degC)') plt.legend(loc='best') plt.xlabel('Time (sec)') plt.savefig('tclab_dyn_meas2.png')

plt.show() (:sourceend:) (:divend:)

1st Order System Identification

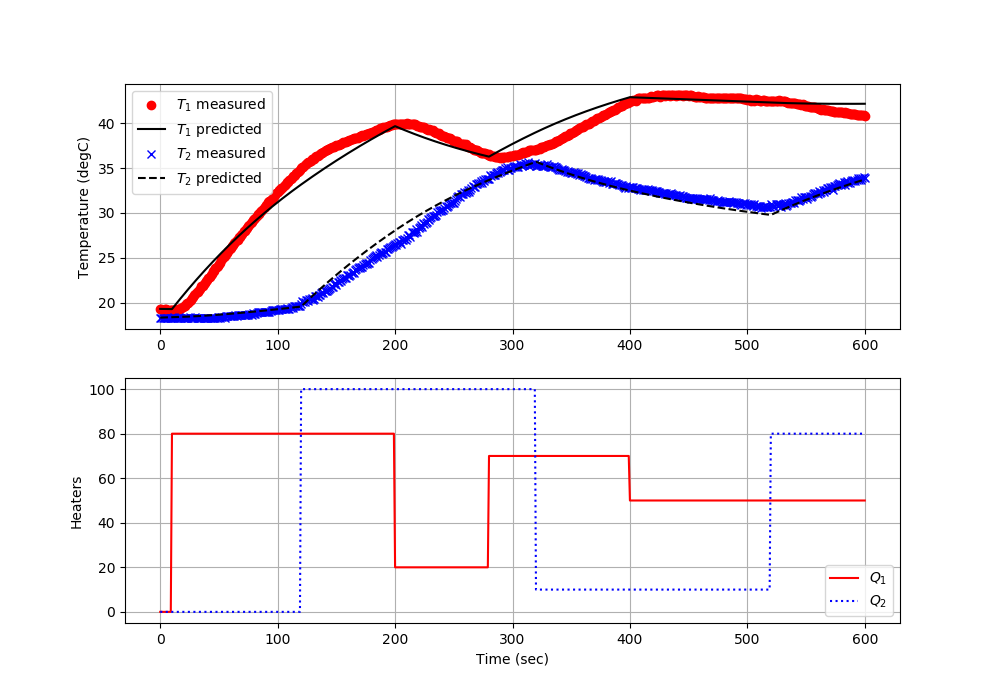
See information on .

(:toggle hide gekko_labD1 button show="Lab D: Python GEKKO 1st Order":) (:div id=gekko_labD1:) import numpy as np import time import matplotlib.pyplot as plt import random

  1. get gekko package with:
  2. pip install gekko

from gekko import GEKKO import pandas as pd

  1. import data

try: 

    # read data file if available
    data = pd.read_csv('tclab_dyn_data2.csv')

except: 

    # retrieve data file from Internet source
    url = 'http://apmonitor.com/do/uploads/Main/tclab_dyn_data2.txt'
    data = pd.read_csv(url)

tm = data['Time'].values Q1s = data['H1'].values # heater 1 Q2s = data['H2'].values # heater 2 T1s = data['T1'].values T2s = data['T2'].values

  1. Initialize Model as Estimator

m = GEKKO(remote=True)

m.time = tm

  1. Parameters to Estimate

K1 = m.FV(value=0.5,lb=0.1,ub=1.0) K2 = m.FV(value=0.3,lb=0.1,ub=1.0) K3 = m.FV(value=0.1,lb=0.0001,ub=1.0) tau12 = m.FV(value=150,lb=50,ub=250)

K1.STATUS = 1 K2.STATUS = 1 K3.STATUS = 1 tau12.STATUS = 1

  1. Measured inputs

Q1 = m.MV(value=Q1s) Q2 = m.MV(value=Q2s)

  1. use measurements

Q1.FSTATUS = 1 # measured Q2.FSTATUS = 1 # measured

  1. Ambient temperature

Ta = m.Param(value=19.0) # degC

  1. Measurements for model alignment

TC1 = m.CV(value=T1s) TC1.STATUS = 1 # minimize error between simulation and measurement TC1.FSTATUS = 1 # receive measurement TC1.MEAS_GAP = 0.1 # measurement deadband gap

TC2 = m.CV(value=T2s) TC2.STATUS = 1 # minimize error between simulation and measurement TC2.FSTATUS = 1 # receive measurement TC2.MEAS_GAP = 0.1 # measurement deadband gap

  1. Heat transfer between two heaters

DT = m.Intermediate(TC2-TC1)

  1. Empirical correlations

m.Equation(tau12 * TC1.dt() + (TC1-Ta) == K1*Q1 + K3*DT) m.Equation(tau12 * TC2.dt() + (TC2-Ta) == K2*Q2 - K3*DT)

  1. Global Options

m.options.IMODE = 5 # MHE m.options.EV_TYPE = 2 # Objective type m.options.NODES = 3 # Collocation nodes m.options.SOLVER = 3 # IPOPT

  1. Predict Parameters and Temperatures

m.solve()

  1. Create plot

plt.figure(figsize=(10,7))

ax=plt.subplot(2,1,1) ax.grid() plt.plot(tm,T1s,'ro',label=r'$T_1$ measured') plt.plot(tm,TC1.value,'k-',label=r'$T_1$ predicted') plt.plot(tm,T2s,'bx',label=r'$T_2$ measured') plt.plot(tm,TC2.value,'k--',label=r'$T_2$ predicted') plt.ylabel('Temperature (degC)') plt.legend(loc=2) ax=plt.subplot(2,1,2) ax.grid() plt.plot(tm,Q1s,'r-',label=r'$Q_1$') plt.plot(tm,Q2s,'b:',label=r'$Q_2$') plt.ylabel('Heaters') plt.xlabel('Time (sec)') plt.legend(loc='best')

  1. Print optimal values

print('K1: ' + str(K1.newval)) print('K2: ' + str(K2.newval)) print('K3: ' + str(K3.newval)) print('tau12: ' + str(tau12.newval))

  1. Save and show figure

plt.savefig('tclab_1st_order.png') plt.show() (:source lang=python:) (:sourceend:) (:divend:)

2nd Order System Identification

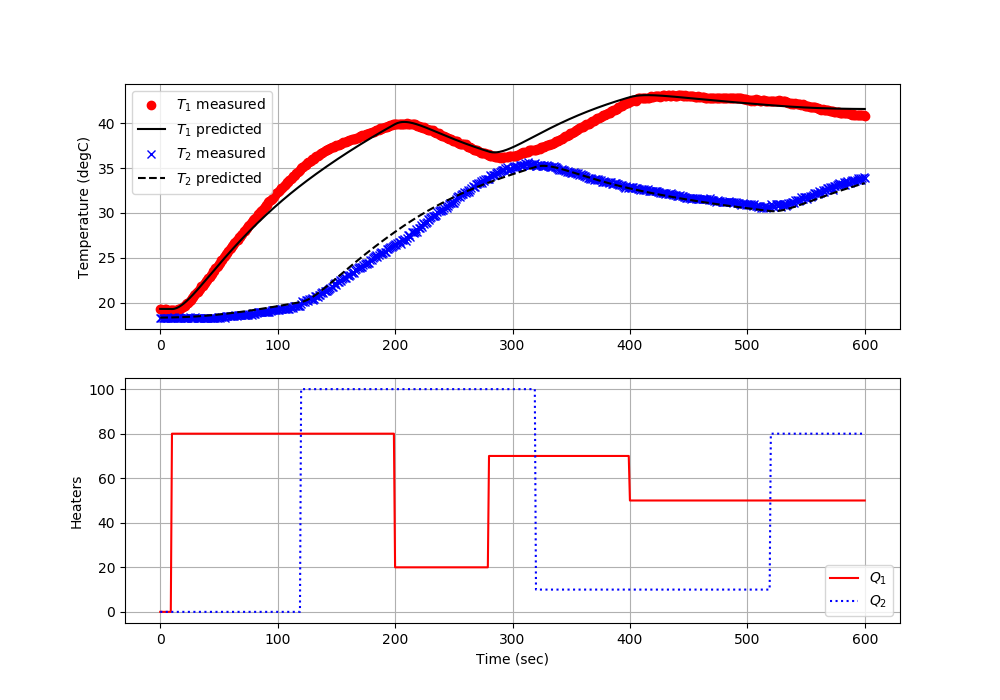
See information on .

(:toggle hide gekko_labD2 button show="Lab D: Python GEKKO 2nd Order":) (:div id=gekko_labD2:) import numpy as np import time import matplotlib.pyplot as plt import random

  1. get gekko package with:
  2. pip install gekko

from gekko import GEKKO import pandas as pd

  1. import data

try: 

    # read data file if available
    data = pd.read_csv('tclab_dyn_data2.csv')

except: 

    # retrieve data file from Internet source
    url = 'http://apmonitor.com/do/uploads/Main/tclab_dyn_data2.txt'
    data = pd.read_csv(url)

tm = data['Time'].values Q1s = data['H1'].values # heater 1 Q2s = data['H2'].values # heater 2 T1s = data['T1'].values T2s = data['T2'].values

  1. Initialize Model as Estimator

m = GEKKO(remote=True)

m.time = tm

  1. Parameters to Estimate

K1 = m.FV(value=0.5,lb=0.1,ub=1.0) K2 = m.FV(value=0.3,lb=0.1,ub=1.0) K3 = m.FV(value=0.1,lb=0.0001,ub=1.0) tau12 = m.FV(value=150,lb=50,ub=250) tau3 = m.FV(value=15,lb=10,ub=20)

K1.STATUS = 1 K2.STATUS = 1 K3.STATUS = 1 tau12.STATUS = 1 tau3.STATUS = 1

  1. Measured inputs

Q1 = m.MV(value=Q1s) Q2 = m.MV(value=Q2s)

  1. use measurements

Q1.FSTATUS = 1 # measured Q2.FSTATUS = 1 # measured

  1. Ambient temperature

Ta = m.Param(value=19.0) # degC

  1. State variables

TH1 = m.SV(value=T1s[0]) TH2 = m.SV(value=T2s[0])

  1. Measurements for model alignment

TC1 = m.CV(value=T1s) TC1.STATUS = 1 # minimize error between simulation and measurement TC1.FSTATUS = 1 # receive measurement TC1.MEAS_GAP = 0.1 # measurement deadband gap

TC2 = m.CV(value=T2s) TC2.STATUS = 1 # minimize error between simulation and measurement TC2.FSTATUS = 1 # receive measurement TC2.MEAS_GAP = 0.1 # measurement deadband gap

  1. Heat transfer between two heaters

DT = m.Intermediate(TH2-TH1)

  1. Empirical correlations

m.Equation(tau12 * TH1.dt() + (TH1-Ta) == K1*Q1 + K3*DT) m.Equation(tau12 * TH2.dt() + (TH2-Ta) == K2*Q2 - K3*DT) m.Equation(tau3 * TC1.dt() + TC1 == TH1) m.Equation(tau3 * TC2.dt() + TC2 == TH2)

  1. Global Options

m.options.IMODE = 5 # MHE m.options.EV_TYPE = 2 # Objective type m.options.NODES = 3 # Collocation nodes m.options.SOLVER = 3 # IPOPT

  1. Predict Parameters and Temperatures

m.solve()

  1. Create plot

plt.figure(figsize=(10,7))

ax=plt.subplot(2,1,1) ax.grid() plt.plot(tm,T1s,'ro',label=r'$T_1$ measured') plt.plot(tm,TC1.value,'k-',label=r'$T_1$ predicted') plt.plot(tm,T2s,'bx',label=r'$T_2$ measured') plt.plot(tm,TC2.value,'k--',label=r'$T_2$ predicted') plt.ylabel('Temperature (degC)') plt.legend(loc=2) ax=plt.subplot(2,1,2) ax.grid() plt.plot(tm,Q1s,'r-',label=r'$Q_1$') plt.plot(tm,Q2s,'b:',label=r'$Q_2$') plt.ylabel('Heaters') plt.xlabel('Time (sec)') plt.legend(loc='best')

  1. Print optimal values

print('K1: ' + str(K1.newval)) print('K2: ' + str(K2.newval)) print('K3: ' + str(K3.newval)) print('tau12: ' + str(tau12.newval)) print('tau3: ' + str(tau3.newval))

  1. Save and show figure

plt.savefig('tclab_2nd_order.png') plt.show() (:source lang=python:) (:sourceend:) (:divend:)

See also:

Advanced Control Lab Overview

Lab A - Single Heater Modeling
Lab B - Dual Heater Modeling
Lab C - Parameter Estimation
Lab D - Empirical Model Estimation
Lab E - Hybrid Model Estimation
Lab F - Linear Model Predictive Control
Lab G - Nonlinear Model Predictive Control
Lab H - Moving Horizon Estimation with MPC

GEKKO Documentation

TCLab Documentation

TCLab Files on GitHub

Basic (PID) Control Lab

(:html:) <style> .button { 

  border-radius: 4px;
  background-color: #0000ff;
  border: none;
  color: #FFFFFF;
  text-align: center;
  font-size: 28px;
  padding: 20px;
  width: 300px;
  transition: all 0.5s;
  cursor: pointer;
  margin: 5px;

}

.button span { 

  cursor: pointer;
  display: inline-block;
  position: relative;
  transition: 0.5s;

}

.button span:after { 

  content: '\00bb';
  position: absolute;
  opacity: 0;
  top: 0;
  right: -20px;
  transition: 0.5s;

}

.button:hover span { 

  padding-right: 25px;

}

.button:hover span:after { 

  opacity: 1;
  right: 0;

} </style> (:htmlend:)

Restore
Streaming Chatbot
💬