Regression Introduction
Regression is used to train a model to predict a relationship between a dependent variable and one or more independent variables. Regression models can be linear or nonlinear, depending on the relationship between the dependent and independent variables. See the Machine Learning for Engineers course for additional information and the following tutorials:
- Linear Regression
- Nonlinear Regression
- Gaussian Processes
- k-Nearest Neighbors
- Neural Network Regressor
- Support Vector Regressor
- XGBoost Regressor
This tutorial is with linear regression to demonstrate a simple example in Python Gekko.
Example Multiple Linear Regression
Multiple linear regression models the relationship between a dependent variable and one or more independent variables. It is used when there are multiple independent variables that contribute to the prediction of the dependent variable. The goal of multiple linear regression is to find the best fit that minimizes the differences between the observed and predicted values of the dependent variable.
Objective: Perform multiple linear regression on sample data with two inputs.
Find unknown parameters c0-c2 to minimize the difference between measured ym and predicted yp subject to a constraint on the summation of c1 x1.
Data
$$x_1 = [1,2,5,3,2,5,2]$$
$$x_2 = [5,6,7,2,1,3,2]$$
$$y_m = [3,2,3,5,6,7,8]$$
Linear Equation
$$y_p = c_0 + c_1 x_1 + c_2 x_2$$
Constraint
$$0 \le \sum_{i=1}^n c_1 x_{1,i} \le 10$$
Minimize Objective
$$\min_{c} \sum_{i=1}^n \left(y_{m,i}-y_{p,i}\right)^2$$
where n is the length of ym and c0-c2 are adjusted to minimize the sum of the squared errors. Report the parameter values and display a plot of the results.
Solution
Python Gekko has a regression mode where the equations are written once and applied over all data rows. The vsum object creates a vertical summation over a column.
from gekko import GEKKO
# load data
x1 = np.array([1,2,5,3,2,5,2])
x2 = np.array([5,6,7,2,1,3,2])
ym = np.array([3,2,3,5,6,7,8])
# model
m = GEKKO()
c = m.Array(m.FV,3)
for ci in c:
ci.STATUS=1
x1 = m.Param(value=x1)
x2 = m.Param(value=x2)
ymeas = m.Param(value=ym)
ypred = m.Var()
m.Equation(ypred == c[0] + c[1]*x1 + c[2]*x2)
# add constraint on sum(c[1]*x1) with vsum
v1 = m.Var(); m.Equation(v1==c[1]*x1)
con = m.Var(lb=0,ub=10); m.Equation(con==m.vsum(v1))
m.Minimize((ypred-ymeas)**2)
m.options.IMODE = 2
m.solve()
print('Final SSE Objective: ' + str(m.options.objfcnval))
print('Solution')
for i,ci in enumerate(c):
print(i,ci.value[0])
# plot solution
import matplotlib.pyplot as plt
plt.figure(figsize=(8,4))
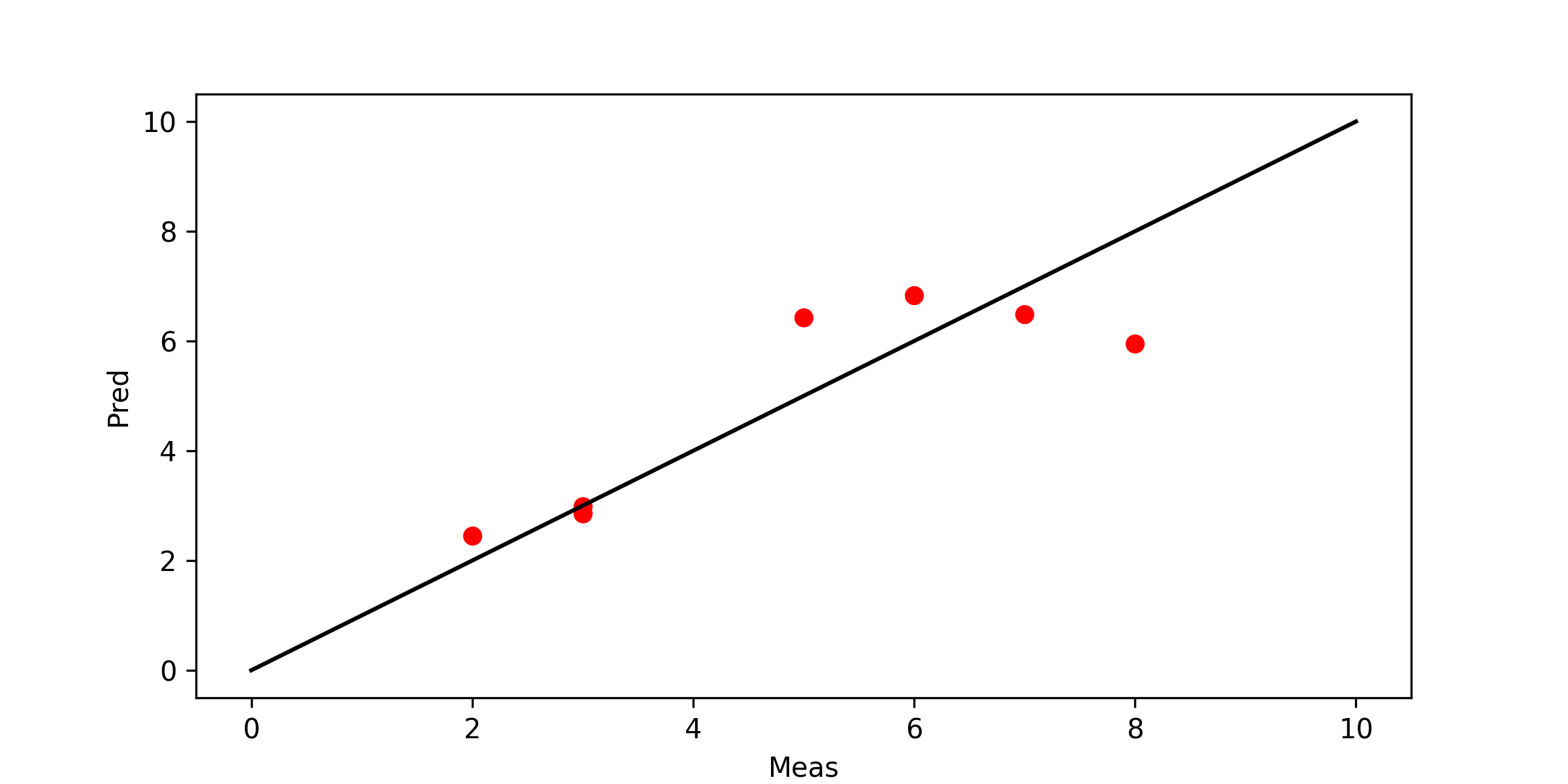
plt.plot(ymeas,ypred,'ro')
plt.plot([0,10],[0,10],'k-')
plt.xlabel('Meas')
plt.ylabel('Pred')
plt.savefig('results.png',dpi=300)
plt.show()
It is also possible to write each equation individually for additional control over the regression form. The IMODE=3 option is for optimization problems where each variable, objective term, and equation are written individually. IMODE=2 is more efficient for large-scale problems.
from gekko import GEKKO
# load data
x1 = np.array([1,2,5,3,2,5,2])
x2 = np.array([5,6,7,2,1,3,2])
ym = np.array([3,2,3,5,6,7,8])
n = len(ym)
# model
m = GEKKO()
c = m.Array(m.FV,3)
for ci in c:
ci.STATUS=1
yp = m.Array(m.Var,n)
for i in range(n):
m.Equation(yp[i]==c[0]+c[1]*x1[i]+c[2]*x2[i])
m.Minimize((yp[i]-ym[i])**2)
# add constraint on sum(c[1]*x1)
s = m.Var(lb=0,ub=10); m.Equation(s==c[1]*sum(x1))
m.options.IMODE = 3
m.solve()
print('Final SSE Objective: ' + str(m.options.objfcnval))
print('Solution')
for i,ci in enumerate(c):
print(i,ci.value[0])
# plot solution
import matplotlib.pyplot as plt
plt.figure(figsize=(8,4))
ypv = [yp[i].value[0] for i in range(n)]
plt.plot(ym,ypv,'ro')
plt.plot([0,10],[0,10],'k-')
plt.xlabel('Meas')
plt.ylabel('Pred')
plt.savefig('results.png',dpi=300)
plt.show()
These examples do not have differential equations to describe dynamic systems. For problems with differential equations, use IMODE=5 instead of IMODE=2.
| Mode (IMODE) | Simulation | Estimation | Control |
|---|---|---|---|
| No Dynamics | 1=Steady-State (SS) | 2=SS Regression (MPU) | 3=SS Optimize (RTO) |
| Dynamic Simultaneous |
4=Simulation (SIM) | 5=Estimation (EST) | 6=Control (CTL) |
| Dynamic Sequential |
7=Simulation (SQS) | 8=Estimation (EST) | 9=Control (CTL) |
See Introduction to Dynamic Estimation Examples 3 and 4 for IMODE=5 with differential equations and the Gekko IMODE Documentation.
