Dynamic Optimization

Model predictive control (MPC) is a type of control algorithm that is used to control systems with dynamics. It is a model-based method that uses a predictive model of the system to compute control actions that optimize a performance criterion over a finite horizon.

The basic idea of MPC is to optimize a control policy that minimizes the difference between the desired reference signal and the output of the system, subject to constraints on the control inputs and the states of the system. This optimization problem can be written as follows:

$$\min_{u_k, ..., u_{k+N-1}} \sum_{i=k}^{k+N-1} ||r_i - y_i||^2 + \sum_{i=k}^{k+N-1} ||u_i - u_{i-1}||^2$$

subject to:

$$x_{k+1} = f(x_k, u_k)$$

$$g_j(x_i, u_i) \leq 0 \quad (j=1,2,...,m)$$

where `u_k,\ldots, u_{k+N-1}` are the control inputs at each time step in the horizon, r_i is the reference signal at time i, y_i is the output of the system at time i, f(x_k, u_k) is the model prediction of the state at time k+1 given the state at time k and the control input at time k, x_k+1 is the state at time k+1, and g_j(x_i, u_i) are the constraints on the states and control inputs at time i.

The optimization problem is solved using an optimization algorithm, such as the interior point method, at each time step. The solution of the optimization problem gives the optimal control inputs for the current time step and the next few time steps in the horizon. The control inputs for the current time step are then applied to the system, and the horizon is shifted forward by one time step. The process is then repeated at the next time step.

MPC has several advantages compared to other control algorithms. It allows the control of systems with constraints on the control inputs and states, it can handle a wide range of performance criteria, and it can handle systems with time-varying dynamics. It is widely used in industries such as chemical process control, automotive control, and power systems.

There are many methods to implement control including basic strategies such as a proportional-integral-derivative (PID) controller or more advanced methods such as model predictive techniques. The purpose of this section is to provide a tutorial overview of potential strategies for control of nonlinear systems with linear models.

A following section relates methods to implement dynamic control with nonlinear models.

Exercise

Objective: Design a model predictive controller for an overhead crane with a pendulum mass. Meet specific control objectives by tuning the controller and using the state space model of the crane system. Simulate and optimize the pendulum system with an adjustable overhead cart. Estimated time: 2 hours.

A pendulum is described by the following dynamic equations:

$$\begin{bmatrix} \dot y \\ \dot v \\ \dot \theta \\ \dot q \end{bmatrix}=\begin{bmatrix} 0 & 1 & 0 & 0\\ 0 & 0 & \epsilon & 0\\ 0 & 0 & 0 & 1\\ 0 & 0 & -1 & 0 \end{bmatrix} \begin{bmatrix} y \\ v \\ \theta \\ q \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \\ 0 \\ -1 \end{bmatrix} u$$

where m₁=10 is the mass of the cart, m₂=1 is the mass of the item carried, `\epsilon` is m₂/(m₁+m₂), y is the position of the overhead cart, v is the velocity of the overhead cart, `\theta` is the angle of the pendulum relative to the cart, and q is the rate of angle change².

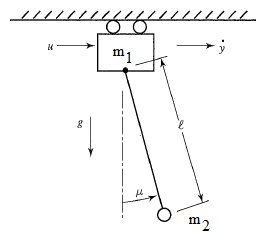
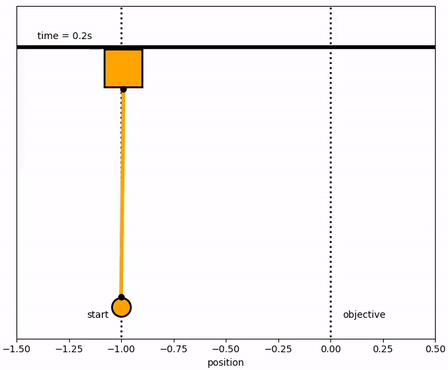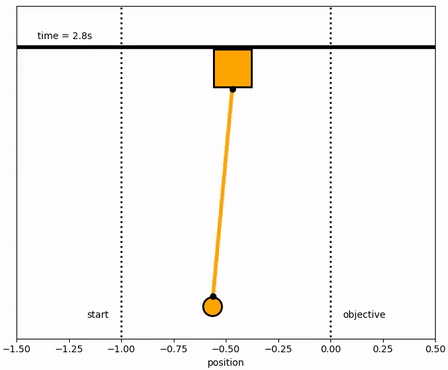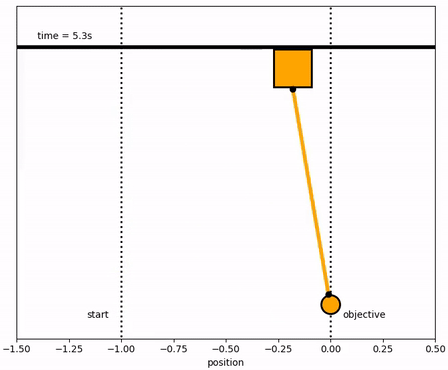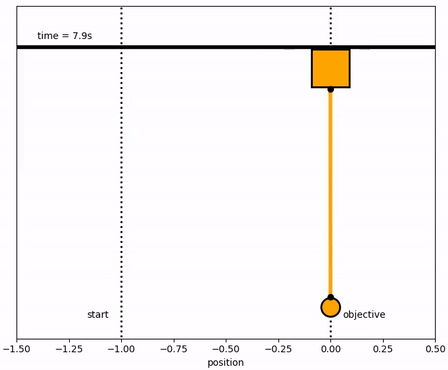
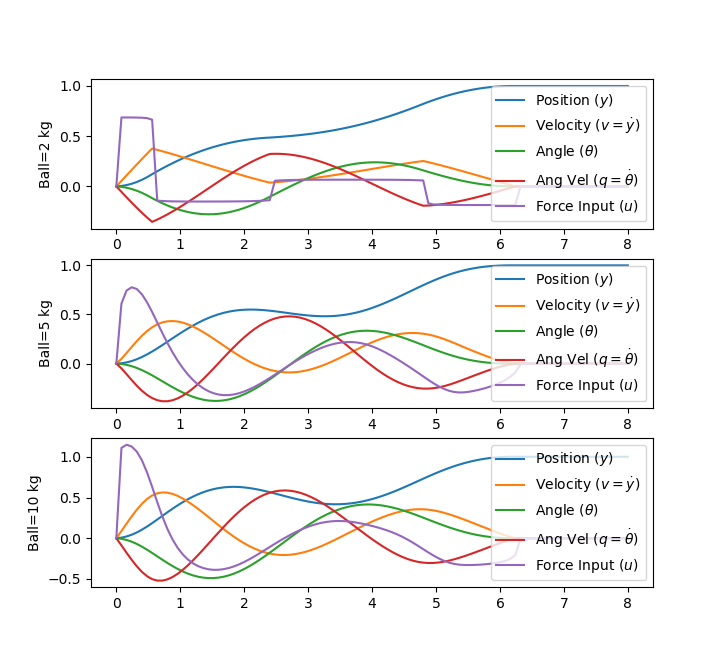
The objective of the controller is to adjust the force on the cart to move the pendulum mass to a new final position. Ensure that initial and final velocities and angles of the pendulum are zero. The position of the pendulum mass is initially at -1 and it is desired to move it to the new position of 0 within 6.2 seconds. Demonstrate controller performance with changes in the pendulum position and that the final pendulum mass remains at the final position without oscillation. How does the solution change if the mass of the item carried is increased to m₂=5?

Solution

Solution with m₂=1

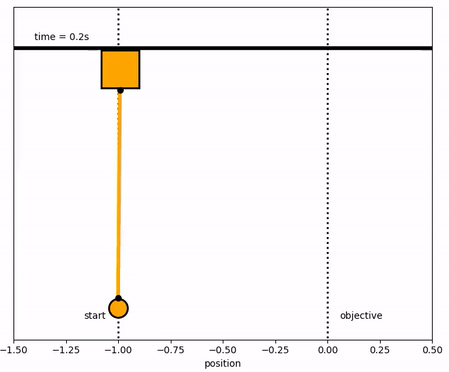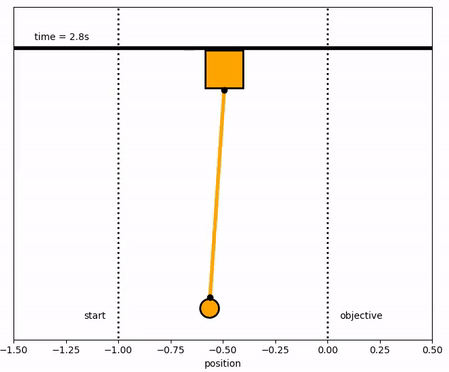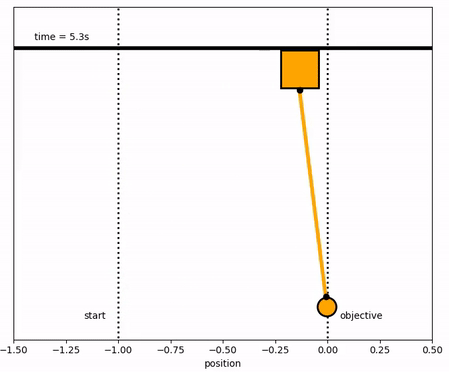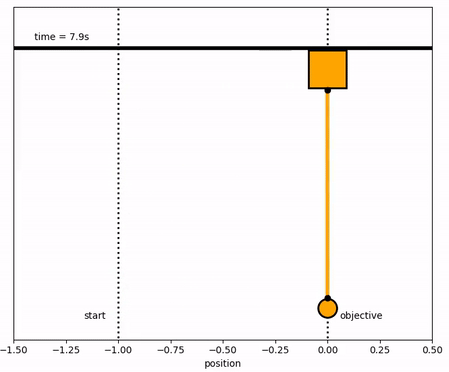
Solution with m₂=5

import numpy as np
from gekko import GEKKO
import matplotlib.pyplot as plt

mass = [2,5,10]
nm = len(mass)
plt.figure()

for j in range(len(mass)):
    m1 = 10
    m2 = mass[j]
    eps = m2/(m1+m2)
    A = np.array([[0,1,0,0],
                 [0,0,eps,0],
                 [0,0,0,1],
                 [0,0,-1,0]])
    B = np.array([[0],
                 [1],
                 [0],
                 [-1]])
    C = np.identity(4)

    m = GEKKO()
    x,y,u = m.state_space(A,B,C,D=None)
    m.time = np.linspace(0,8,101)
    fn = [0 if m.time[i]<6.2 else 1 for i in range(101)]      
    final = m.Param(value=fn)
    u[0].status = 1
    m.Obj(final * ((y[0]-1)**2 + y[1]**2 + y[2]**2 + y[3]**2))    
    m.options.IMODE = 6
    m.solve()

    plt.subplot(len(mass),1,j+1)
    plt.ylabel(f'Ball={mass[j]} kg')
    plt.plot(m.time,y[0], label = r"Position ($y$)")
    plt.plot(m.time,y[1], label = r"Velocity ($v=\dot y$)")
    plt.plot(m.time,y[2], label = r"Angle ($\theta$)")
    plt.plot(m.time,y[3], label = r"Ang Vel ($q=\dot \theta$)")
    plt.plot(m.time,u[0], label = r"Force Input ($u$)")
    plt.legend(loc=1)
plt.show()

[$[Get Code]]

Thanks to Derek Prestwich for the state space implementation.

Crane Pendulum Solution Files in MATLAB and Python

References

1. Bryson, A.E., Dynamic Optimization, Addison-Wesley, 1999.