Economic Model Predictive Control (MPC)

Objective: Set up and solve the commercial fishing economic optimal control problem. Create a program to optimize and display the results. Estimated Time: 30 minutes

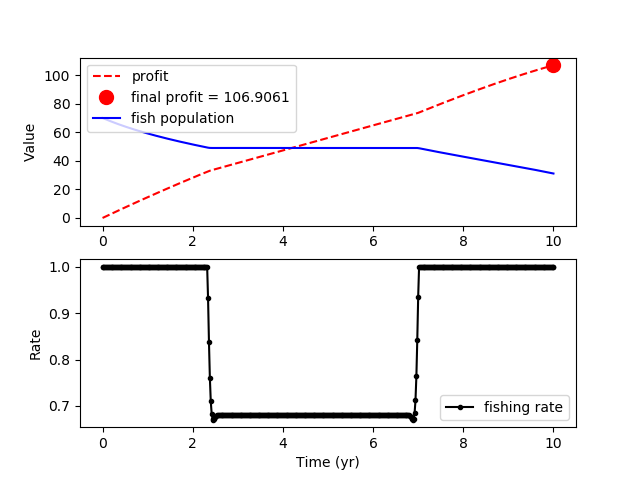
The commercial fishing optimal control problem has an integral profit function that includes the cost of operations and the revenue from fish sales. The population of fish x is influenced by how many fish are removed each year that depends on u. The objective is to maximize the revenue from fishing over a 10 year time period. If there is overfishing (high u) then the returns for subsequent years are reduced and the fish population does not recover. This optimal control problem finds the optimal extraction profile to maximize the commercial fishing profit.

from gekko import GEKKO
import numpy as np
import matplotlib.pyplot as plt

# create GEKKO model
m = GEKKO()

# time points
n=501
m.time = np.linspace(0,10,n)

# constants
E = 1
c = 17.5
r = 0.71
k = 80.5
U_max = 20

# fishing rate
u = m.MV(value=1,lb=0,ub=1)
u.STATUS = 1
u.DCOST = 0

# fish population
x = m.Var(value=70)

# fish population balance
m.Equation(x.dt() == r*x*(1-x/k)-u*U_max)

# objective (profit)
J = m.Var(value=0)
# final objective
Jf = m.FV()
Jf.STATUS = 1
m.Connection(Jf,J,pos2='end')
m.Equation(J.dt() == (E-c/x)*u*U_max)
# maximize profit
m.Maximize(Jf)

# options
m.options.IMODE = 6 # optimal control
m.options.NODES = 3 # collocation nodes
m.options.SOLVER = 3 # solver (IPOPT)

# solve optimization problem
m.solve()

# print profit
print('Optimal Profit: ' + str(Jf.value[0]))

# plot results
plt.figure(1)
plt.subplot(2,1,1)
plt.plot(m.time,J.value,'r--',label='profit')
plt.plot(m.time[-1],Jf.value[0],'ro',markersize=10,\
label='final profit = '+str(Jf.value[0]))
plt.plot(m.time,x.value,'b-',label='fish population')
plt.ylabel('Value')
plt.legend()
plt.subplot(2,1,2)
plt.plot(m.time,u.value,'k.-',label='fishing rate')
plt.ylabel('Rate')
plt.xlabel('Time (yr)')
plt.legend()
plt.show()

[$[Get Code]]

Integrals are a natural expression of many systems where the accumulation of a quantity is maximized or minimized. The integral is the profit function over the 10 year time period.

$$\max_{u(t)} \int_0^{10} \left(E-\frac{c}{x}\right) u \, U_{max} \, dt$$ $$\mathrm{subject \; to}$$ $$\frac{dx}{dt}=r \, x(t) \left(1-\frac{x(t)}{k}\right)-u \, U_{max}$$ $$x(0) = 70$$ $$0 \le u(t) \le 1$$ $$E=1, \, c=17.5, \, r=0.71, \, k=80.5, \, U_{max}=20$$

Integral expressions are reformulated in differential and algebraic form by defining a new variable.

$$J = \int_0^{10} \left(E-\frac{c}{x}\right) u \, U_{max} \, dt$$

The new variable J and integral are differentiated and included as an additional equation. The problem then becomes a maximization of the new variable J at the final time.

$$\max_{u(t)} J\left(t_f\right)$$ $$\mathrm{subject \; to}$$ $$\frac{dx}{dt}=r \, x(t) \left(1-\frac{x(t)}{k}\right)-u \, U_{max}$$ $$\frac{dJ}{dt} = \left(E-\frac{c}{x}\right) u \, U_{max}$$ $$x(0) = 70$$ $$J(0) = 0$$ $$0 \le u(t) \le 1$$ $$t_f = 10, \, E=1, \, c=17.5, \, r=0.71, \, k=80.5, \, U_{max}=20$$

The initial condition of the integral J starts at zero and becomes the integral in the time range of 0 to 10. The end value is maximized at the final point in the time horizon of the optimal control problem. A maximization problem is converted to a minimization problem by multiplying the objective by negative one.

$$\max_{u(t)} J\left(t_f\right) = -\min_{u(t)} J\left(t_f\right)$$

Most optimization solvers require an objective function minimization, including GEKKO and APMonitor.

Solutions in APM MATLAB and APM Python

Economic Optimization of Fishery in MATLAB and Python

References

Beal, L., GEKKO for Dynamic Optimization, 2018, URL: https://gekko.readthedocs.io/en/latest/
Hedengren, J. D. and Asgharzadeh Shishavan, R., Powell, K.M., and Edgar, T.F., Nonlinear Modeling, Estimation and Predictive Control in APMonitor, Computers and Chemical Engineering, Volume 70, pg. 133–148, 2014. Article

Dynamic Optimization