Practice Final Exam
Solution 1
import numpy as np
from gekko import GEKKO
# Check solution with GEKKO
m = GEKKO()
m.time=[0,1]
u = m.Var(value=1)
x = m.Var(value=0)
m.Obj((x-3)**2)
m.Equation(5*x.dt()==-x+2*u)
m.options.IMODE = 6
m.options.NODES = 3
m.solve()
# Matrix solution for Orthogonal Collocation on Finite Elements
#
# min (x-3)^2
# s.t. 5 * dx/dt = -x + 2 * u
#
# Equations 1-2 (subject to equations at each node)
# 5 * xdot1 = -x1 + 2*u1
# 5 * xdot2 = -x2 + 2*u2
# Equations 3-4 (collocation equations)
# t2 * 0.75 * xdot1 - t2 * 0.25 * xdot2 = x1 - x0
# t2 * 1.00 * xdot1 = x2 - x0
# Equations 5-6 (derivative of objective = 0)
# 2 * (x1-3) = 0
# 2 * (x2-3) = 0
#
# Rearrange to put all variables on left-hand side
# Equations 1-2 (subject to equations at each node)
# 5 * xdot1 + x1 - 2*u1 = 0
# 5 * xdot2 + x2 - 2*u2 = 0
# Equations 3-4 (collocation equations)
# t2 * 0.75 * xdot1 - t2 * 0.25 * xdot2 - x1 = -x0
# t2 * 1.00 * xdot1 - x2 = -x0
# Equations 5-6 (derivative of objective = 0)
# 2 * x1 = 6
# 2 * x2 = 6
#
# Set-up and solve A y = b
# y = [xdot1 xdot2 x1 x2 u1 u2]
# Matrix A
A = np.array([[5,0,1,0,-2,0],\
[0,5,0,1,0,-2],\
[0.75,-0.25,-1,0,0,0],\
[1,0,0,-1,0,0],\
[0,0,2,0,0,0],\
[0,0,0,2,0,0]])
# Column vector b
b = np.array([0,0,0,0,6,6])
# Solve A y = b as y = A^-1 * b
ymat = np.linalg.solve(A,b)
print('Variables with Orthogonal Collocation')
print(['u1 = ' + str(ymat[4])])
print(['u2 = ' + str(ymat[5]) + \
' (Matrix) vs ' + str(u.value[-1]) + ' (GEKKO)'])
print(['x1 = ' + str(ymat[2])])
print(['x2 = ' + str(ymat[3]) + \
' (Matrix) vs ' + str(x.value[-1]) + ' (GEKKO)'])
print(' ')
print('Derivatives with Orthogonal Collocation')
print(['d(x11)/dt = ' + str(ymat[0])])
print(['d(x21)/dt = ' + str(ymat[1])])
from gekko import GEKKO
# Check solution with GEKKO
m = GEKKO()
m.time=[0,1]
u = m.Var(value=1)
x = m.Var(value=0)
m.Obj((x-3)**2)
m.Equation(5*x.dt()==-x+2*u)
m.options.IMODE = 6
m.options.NODES = 3
m.solve()
# Matrix solution for Orthogonal Collocation on Finite Elements
#
# min (x-3)^2
# s.t. 5 * dx/dt = -x + 2 * u
#
# Equations 1-2 (subject to equations at each node)
# 5 * xdot1 = -x1 + 2*u1
# 5 * xdot2 = -x2 + 2*u2
# Equations 3-4 (collocation equations)
# t2 * 0.75 * xdot1 - t2 * 0.25 * xdot2 = x1 - x0
# t2 * 1.00 * xdot1 = x2 - x0
# Equations 5-6 (derivative of objective = 0)
# 2 * (x1-3) = 0
# 2 * (x2-3) = 0
#
# Rearrange to put all variables on left-hand side
# Equations 1-2 (subject to equations at each node)
# 5 * xdot1 + x1 - 2*u1 = 0
# 5 * xdot2 + x2 - 2*u2 = 0
# Equations 3-4 (collocation equations)
# t2 * 0.75 * xdot1 - t2 * 0.25 * xdot2 - x1 = -x0
# t2 * 1.00 * xdot1 - x2 = -x0
# Equations 5-6 (derivative of objective = 0)
# 2 * x1 = 6
# 2 * x2 = 6
#
# Set-up and solve A y = b
# y = [xdot1 xdot2 x1 x2 u1 u2]
# Matrix A
A = np.array([[5,0,1,0,-2,0],\
[0,5,0,1,0,-2],\
[0.75,-0.25,-1,0,0,0],\
[1,0,0,-1,0,0],\
[0,0,2,0,0,0],\
[0,0,0,2,0,0]])
# Column vector b
b = np.array([0,0,0,0,6,6])
# Solve A y = b as y = A^-1 * b
ymat = np.linalg.solve(A,b)
print('Variables with Orthogonal Collocation')
print(['u1 = ' + str(ymat[4])])
print(['u2 = ' + str(ymat[5]) + \
' (Matrix) vs ' + str(u.value[-1]) + ' (GEKKO)'])
print(['x1 = ' + str(ymat[2])])
print(['x2 = ' + str(ymat[3]) + \
' (Matrix) vs ' + str(x.value[-1]) + ' (GEKKO)'])
print(' ')
print('Derivatives with Orthogonal Collocation')
print(['d(x11)/dt = ' + str(ymat[0])])
print(['d(x21)/dt = ' + str(ymat[1])])
Solution 2
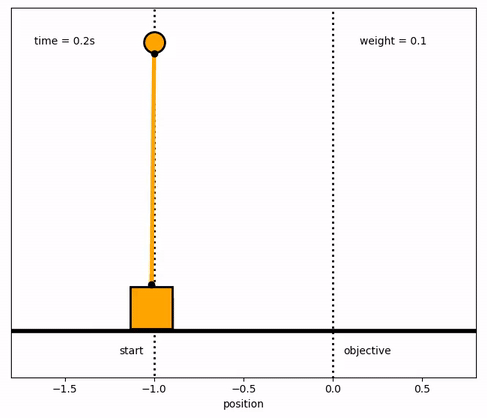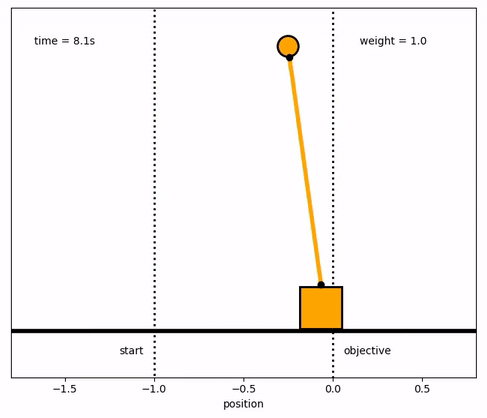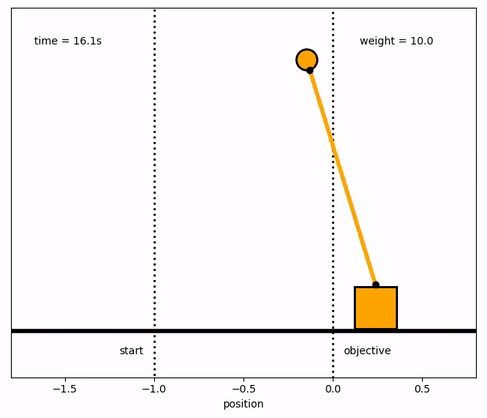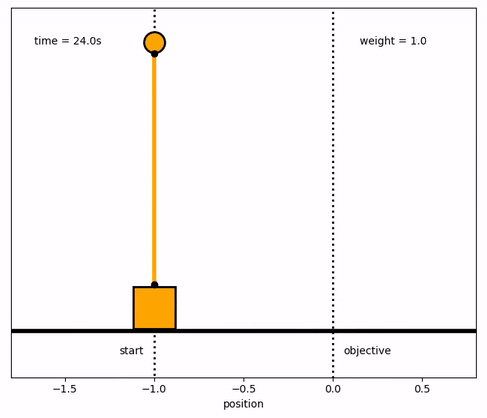
 See Level Control
See Level Control