Practice Midterm Exam 3
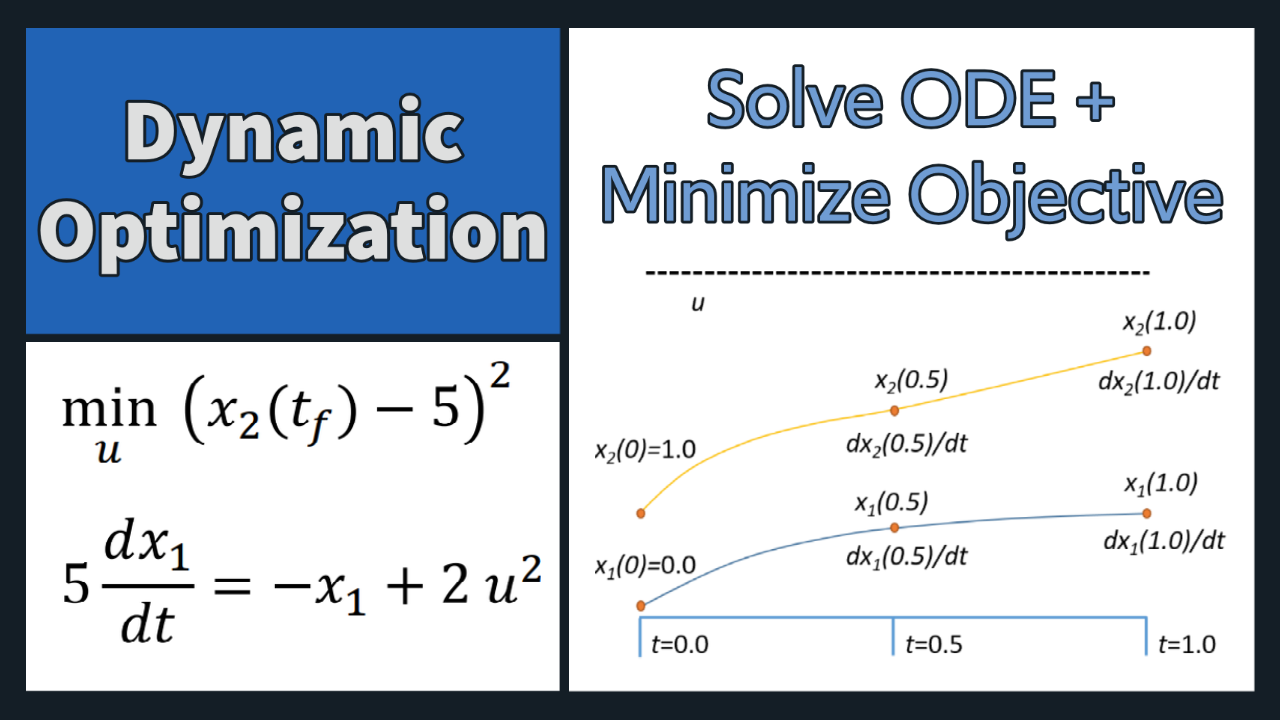
Problem 1 Solution (Orthogonal Collocation)
from gekko import GEKKO
import numpy as np
m = GEKKO(remote=False)
x10 = 0; x20 = 1
u, x11, x12, x21, x22, dx11, dx12, dx21, dx22 = m.Array(m.Var,9)
u.value = 1; x11.value = 1; x12.value = 1; x21.value = 1; x22.value = 1
N = np.array([[0.75, -0.25],\
[1.00, 0.00]])
m.Equations([np.dot(N[0],[dx11, dx12]) == x11 - x10,
np.dot(N[1],[dx11, dx12]) == x12 - x10,
np.dot(N[0],[dx21, dx22]) == x21 - x20,
np.dot(N[1],[dx21, dx22]) == x22 - x20,
5*dx11 == -x11 + 2*u**2,
5*dx12 == -x12 + 2*u**2,
3*dx21 == -x21 + x11**2,
3*dx22 == -x22 + x12**2,
x22-5 == 0])
m.solve(disp=False)
print(u[0])
print(x10, x11[0], x12[0])
print(x20, x21[0], x22[0])
print(dx11[0], dx12[0], dx21[0], dx22[0])
import numpy as np
m = GEKKO(remote=False)
x10 = 0; x20 = 1
u, x11, x12, x21, x22, dx11, dx12, dx21, dx22 = m.Array(m.Var,9)
u.value = 1; x11.value = 1; x12.value = 1; x21.value = 1; x22.value = 1
N = np.array([[0.75, -0.25],\
[1.00, 0.00]])
m.Equations([np.dot(N[0],[dx11, dx12]) == x11 - x10,
np.dot(N[1],[dx11, dx12]) == x12 - x10,
np.dot(N[0],[dx21, dx22]) == x21 - x20,
np.dot(N[1],[dx21, dx22]) == x22 - x20,
5*dx11 == -x11 + 2*u**2,
5*dx12 == -x12 + 2*u**2,
3*dx21 == -x21 + x11**2,
3*dx22 == -x22 + x12**2,
x22-5 == 0])
m.solve(disp=False)
print(u[0])
print(x10, x11[0], x12[0])
print(x20, x21[0], x22[0])
print(dx11[0], dx12[0], dx21[0], dx22[0])
Problem 2 Solution (Dynamic Optimization)
from gekko import GEKKO
import matplotlib.pyplot as plt
import numpy as np
# Initialize Model
m = GEKKO()
nt = 101
m.time = np.linspace(0,1,nt)
# Parameters
u = m.MV(value=-6)
u.STATUS = 1
# Variables
x = m.Var(value=0,ub=1/9)
v = m.Var(value=1)
J = m.Intermediate(0.5*m.integral(u**2))
p = np.zeros(nt)
p[-1] = 1.0
final = m.Param(value=p)
# Equations
m.Equation(x.dt() == v)
m.Equation(v.dt() == u)
m.Equation(final*x==0)
m.Equation(final*(v+1)==0)
# ,or
# m.Minimize(final*1e5*x**2)
# m.Minimize(final*1e5*(v+1)**2)
# Objective Function
m.Minimize(final*J)
# Options
m.options.IMODE = 6
m.options.NODES = 2
m.options.SOLVER = 1
m.solve(disp=False)
print('Final Objective Function Value:', J.value[-1])
# Create a figure
plt.figure(figsize=(10,4))
plt.subplot(2,2,1)
plt.plot([0,1],[1/9,1/9],'r:',label=r'$x<\frac{1}{9}$')
plt.plot(m.time,x.value,'k-',lw=2,label=r'$x$')
plt.ylabel('Position')
plt.legend(loc='best')
plt.subplot(2,2,2)
plt.plot(m.time,v.value,'b--',lw=2,label=r'$v$')
plt.ylabel('Velocity')
plt.legend(loc='best')
plt.subplot(2,2,3)
plt.plot(m.time,u.value,'r--',lw=2,label=r'$u$')
plt.ylabel('Thrust')
plt.legend(loc='best')
plt.xlabel('Time')
plt.subplot(2,2,4)
plt.plot(m.time,J.value,'g-',lw=2,label=r'$\frac{1}{2} \int u^2$')
plt.text(0.5,3.0,'Final Value = '+str(np.round(J.value[-1],2)))
plt.ylabel('Objective')
plt.legend(loc='best')
plt.xlabel('Time')
plt.show()
import matplotlib.pyplot as plt
import numpy as np
# Initialize Model
m = GEKKO()
nt = 101
m.time = np.linspace(0,1,nt)
# Parameters
u = m.MV(value=-6)
u.STATUS = 1
# Variables
x = m.Var(value=0,ub=1/9)
v = m.Var(value=1)
J = m.Intermediate(0.5*m.integral(u**2))
p = np.zeros(nt)
p[-1] = 1.0
final = m.Param(value=p)
# Equations
m.Equation(x.dt() == v)
m.Equation(v.dt() == u)
m.Equation(final*x==0)
m.Equation(final*(v+1)==0)
# ,or
# m.Minimize(final*1e5*x**2)
# m.Minimize(final*1e5*(v+1)**2)
# Objective Function
m.Minimize(final*J)
# Options
m.options.IMODE = 6
m.options.NODES = 2
m.options.SOLVER = 1
m.solve(disp=False)
print('Final Objective Function Value:', J.value[-1])
# Create a figure
plt.figure(figsize=(10,4))
plt.subplot(2,2,1)
plt.plot([0,1],[1/9,1/9],'r:',label=r'$x<\frac{1}{9}$')
plt.plot(m.time,x.value,'k-',lw=2,label=r'$x$')
plt.ylabel('Position')
plt.legend(loc='best')
plt.subplot(2,2,2)
plt.plot(m.time,v.value,'b--',lw=2,label=r'$v$')
plt.ylabel('Velocity')
plt.legend(loc='best')
plt.subplot(2,2,3)
plt.plot(m.time,u.value,'r--',lw=2,label=r'$u$')
plt.ylabel('Thrust')
plt.legend(loc='best')
plt.xlabel('Time')
plt.subplot(2,2,4)
plt.plot(m.time,J.value,'g-',lw=2,label=r'$\frac{1}{2} \int u^2$')
plt.text(0.5,3.0,'Final Value = '+str(np.round(J.value[-1],2)))
plt.ylabel('Objective')
plt.legend(loc='best')
plt.xlabel('Time')
plt.show()
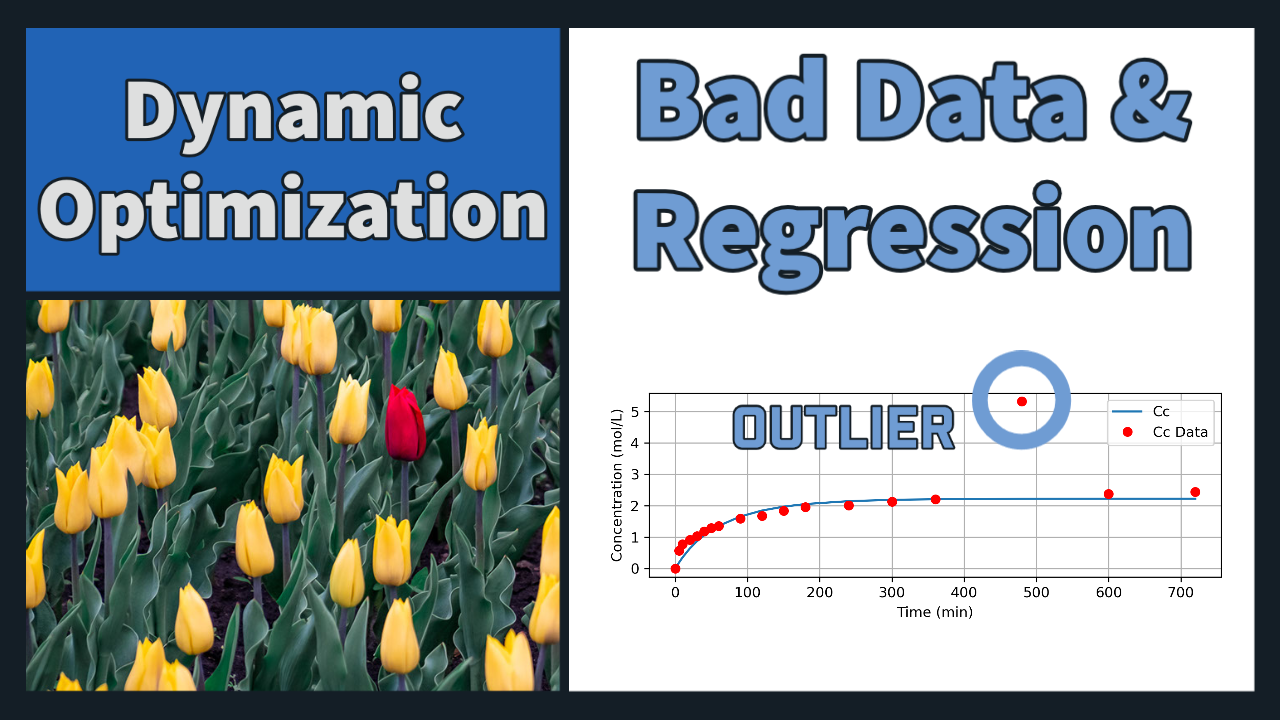
Problem 3 Solution (Regression with Outlier)
import numpy as np
from gekko import GEKKO
import matplotlib.pyplot as plt
#data from problem statement
time = np.array([0, 5, 10, 20, 30, 40, 50, 60, 90, 120,
150, 180, 240, 300, 360, 480, 600, 720])
Cc_meas = np.array([0,0.57, 0.78, 0.92, 1.04, 1.19, 1.29,
1.36, 1.59, 1.68, 1.84, 1.96, 2.01, 2.13,
2.21, 5.32, 2.38, 2.44])
m = GEKKO(remote=True)
m.time = time
Kf = m.FV(value =0.0025, lb = 0, ub = 0.01)
Kb = m.FV(value =0.0025, lb = 0, ub = 0.01)
Kf.STATUS = 1
Kb.STATUS = 1
Ca = m.Var(value = 4.84)
Cb = m.Var(value = 9.67)
Cd = m.Var(value = 0)
Cc = m.CV(Cc_meas)
Cc.FSTATUS = 1
#Reaction equations
m.Equation(Cc.dt() == Kf*Ca*(Cb**2) - Kb*Cc*Cd)
m.Equation(Ca.dt() == -Cc.dt())
m.Equation(Cb.dt() == -2*Cc.dt())
m.Equation(Cd.dt() == Cc.dt())
#turn GEKKO mode to estimation
m.options.IMODE = 5
m.options.NODES = 4
m.options.EV_TYPE = 1 #2 = Sum of squared error, 1 = Sum of absoluted error
m.solve(disp=False)
#solve and plot
plt.figure()
plt.subplot(2,1,1)
plt.plot(m.time, Ca.value, label = 'Ca')
plt.plot(m.time, Cb.value, label = 'Cb')
plt.ylabel('Concentration (mol/L)')
plt.legend(); plt.grid()
plt.subplot(2,1,2)
plt.plot(m.time, Cc.value, label = 'Cc')
plt.plot(m.time, Cc_meas, 'ro', label = 'Cc Data')
plt.ylabel('Concentration (mol/L)')
plt.xlabel('Time (min)')
plt.legend(); plt.grid()
plt.ylabel('Concentration (mol/L)')
plt.tight_layout()
plt.savefig('regression.png',dpi=300)
print("Kf = " + str(Kf.value[0]))
print("Kb = " + str(Kb.value[0]))
from gekko import GEKKO
import matplotlib.pyplot as plt
#data from problem statement
time = np.array([0, 5, 10, 20, 30, 40, 50, 60, 90, 120,
150, 180, 240, 300, 360, 480, 600, 720])
Cc_meas = np.array([0,0.57, 0.78, 0.92, 1.04, 1.19, 1.29,
1.36, 1.59, 1.68, 1.84, 1.96, 2.01, 2.13,
2.21, 5.32, 2.38, 2.44])
m = GEKKO(remote=True)
m.time = time
Kf = m.FV(value =0.0025, lb = 0, ub = 0.01)
Kb = m.FV(value =0.0025, lb = 0, ub = 0.01)
Kf.STATUS = 1
Kb.STATUS = 1
Ca = m.Var(value = 4.84)
Cb = m.Var(value = 9.67)
Cd = m.Var(value = 0)
Cc = m.CV(Cc_meas)
Cc.FSTATUS = 1
#Reaction equations
m.Equation(Cc.dt() == Kf*Ca*(Cb**2) - Kb*Cc*Cd)
m.Equation(Ca.dt() == -Cc.dt())
m.Equation(Cb.dt() == -2*Cc.dt())
m.Equation(Cd.dt() == Cc.dt())
#turn GEKKO mode to estimation
m.options.IMODE = 5
m.options.NODES = 4
m.options.EV_TYPE = 1 #2 = Sum of squared error, 1 = Sum of absoluted error
m.solve(disp=False)
#solve and plot
plt.figure()
plt.subplot(2,1,1)
plt.plot(m.time, Ca.value, label = 'Ca')
plt.plot(m.time, Cb.value, label = 'Cb')
plt.ylabel('Concentration (mol/L)')
plt.legend(); plt.grid()
plt.subplot(2,1,2)
plt.plot(m.time, Cc.value, label = 'Cc')
plt.plot(m.time, Cc_meas, 'ro', label = 'Cc Data')
plt.ylabel('Concentration (mol/L)')
plt.xlabel('Time (min)')
plt.legend(); plt.grid()
plt.ylabel('Concentration (mol/L)')
plt.tight_layout()
plt.savefig('regression.png',dpi=300)
print("Kf = " + str(Kf.value[0]))
print("Kb = " + str(Kb.value[0]))