LSTM Networks
Main.LSTMNetwork History
Show minor edits - Show changes to markup

(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/u7-71upCykM" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> (:htmlend:)
(:divend:)
(:divend:)

(:toggle hide lstm_deploy button show="Show Deployment Solution":) (:div id=lstm_deploy:)
(:toggle hide lstm_deploy button show="Show Deployment Solution":) (:div id=lstm_deploy:)


(:toggle hide lstm_deploy button show="Show Deployment Solution":) (:div id=lstm_deploy:)
Deployment Solution with LSTM Network
Training and testing are often performed once on a dedicated computing platform. The trained model is then packaged for another computing system for predictions as a deployed machine learning solution. The final step of this exercise is to deploy the LSTM controller, independent of the training program. The controller (configuration in lstm_control.pkl and model in lstm_control.h5) can be deployed on embedded architectures without optimizers. Switch to use the TCLab hardware with tclab_hardware = True. Otherwise, the script uses the digital twin simulator.
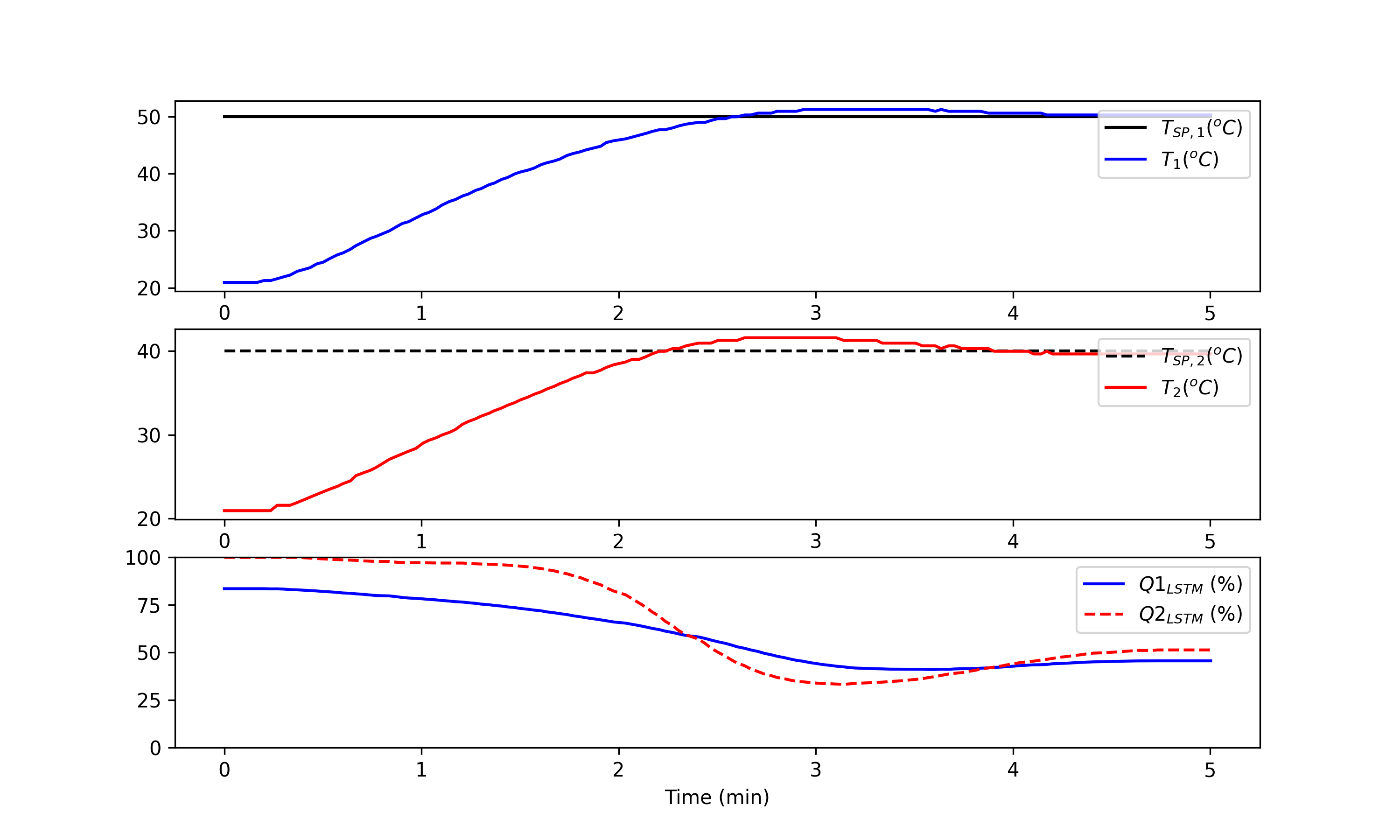
(:source lang=python:) import tclab import time import numpy as np import matplotlib.pyplot as plt import pickle from keras.models import load_model
- PID: 1 sec, MPC: 2 sec
cycle_time = 2 tclab_hardware = False # switch to True if hardware available
h5_file,s_x,s_y,window = pickle.load(open('lstm_control.pkl','rb')) model = load_model(h5_file)
if tclab_hardware:
mlab = tclab.TCLab # Physical hardware
else:
mlab = tclab.setup(connected=False,speedup=10) # Emulator
- LSTM Controller
def lstm(T1_m,Tsp1_m,T2_m,Tsp2_m):
# Calculate error (necessary feature for LSTM input)
err1 = Tsp1_m - T1_m
err2 = Tsp2_m - T2_m
# Format data for LSTM input
X = np.vstack((Tsp1_m,err1,Tsp2_m,err2)).T
Xs = s_x.transform(X)
Xs = np.reshape(Xs, (1, Xs.shape[0], Xs.shape[1]))
# Predict Q for controller and unscale
Qc_s = model.predict(Xs)
Qc = s_y.inverse_transform(Qc_s)[0]
# Ensure Qc is between 0 and 100
Qc = np.clip(Qc,0.0,100.0)
return Qc
tf = 300 # final time (sec) n = int(tf/cycle_time) # cycles tm=[]; T1=[]; T2=[]; Q1=[]; Q2=[] # storage
lab = mlab() i = 0 for t in tclab.clock(tf, cycle_time):
# record time
tm.append(t)
# read temperatures
T1.append(lab.T1)
T2.append(lab.T2)
# LSTM control
if i>=window:
T1_m = T1[i-window:i]
T2_m = T2[i-window:i]
else:
insert1 = np.ones(window-i)*T1[0]
insert2 = np.ones(window-i)*T2[0]
T1_m = np.concatenate((insert1,T1[0:-1]))
T2_m = np.concatenate((insert2,T2[0:-1]))
Tsp1_m = 50*np.ones(window)
Tsp2_m = 40*np.ones(window)
Q = lstm(T1_m,Tsp1_m,T2_m,Tsp2_m)
Q1.append(Q[0]); Q2.append(Q[1])
lab.Q1(Q1[-1]); lab.Q2(Q2[-1])
if i%50==0:
print(' Time_____Q1___Tsp1_____T1_____Q2___Tsp2_____T2')
if i%5==0:
s='{:6.1f} {:6.2f} {:6.2f} {:6.2f} {:6.2f} {:6.2f} {:6.2f}'
print((s).format(tm[-1],Q1[-1],Tsp1_m[-1],T1[-1], Q2[-1],Tsp2_m[-1],T2[-1]))
i+=1
lab.close()
- Create Figure
tmin = np.array(tm)/60.0 plt.figure(figsize=(10,6)) plt.subplot(3,1,1) plt.plot(tmin,np.ones_like(tmin)*50,'k-',label='$T_{SP,1} (^oC)$') plt.plot(tmin,T1,'b-',label='$T_1 (^oC)$') plt.legend(loc=1) plt.subplot(3,1,2) plt.plot(tmin,np.ones_like(tmin)*40,'k--',label='$T_{SP,2} (^oC)$') plt.plot(tmin,T2,'r-',label='$T_2 (^oC)$') plt.legend(loc=1) plt.subplot(3,1,3) plt.plot(tmin,Q1,'b-',label='$Q1_{LSTM}$ (%)') plt.plot(tmin,Q2,'r--',label='$Q2_{LSTM}$ (%)') plt.legend(loc=1) plt.ylim([0,100]) plt.xlabel('Time (min)') plt.savefig('LSTM_Control.png',dpi=300) plt.show() (:sourceend:) (:divend:)
 LSTM Automation MIMO MPC Case Study Notebook
LSTM Automation MIMO MPC Case Study Notebook Jupyter Notebook in Google Colab
Jupyter Notebook in Google ColabModel Predictive Control (MPC) is applied online with real-time optimizers that coordinate control moves. This case study demonstrates training and replacement of the MPC with an LSTM network. Two prior case studies demonstrate this same approach with PID control and SISO (Single Input, Single Output) MPC. In this case study, the LSTM network is trained from a 2x2 MIMO MPC (Single Input Single Output, Model Predictive Control). LSTM (Long Short Term Memory) networks are a special type of RNN (Recurrent Neural Network) that is structured to remember and predict based on long-term dependencies that are trained with time-series data.
Model Predictive Control (MPC) is applied online with real-time optimizers that coordinate control moves. This case study demonstrates training and replacement of the MPC with an LSTM network. Two prior case studies demonstrate this same approach with an LSTM Network Replacing PID control and SISO (Single Input, Single Output) MPC. In this case study, the LSTM network is trained from a 2x2 MIMO MPC (Single Input Single Output, Model Predictive Control). LSTM (Long Short Term Memory) networks are a special type of RNN (Recurrent Neural Network) that is structured to remember and predict based on long-term dependencies that are trained with time-series data.
Exercise 2: LSTM Emulates MIMO MPC
Exercise 2: LSTM Replaces MIMO MPC
Exercise
Exercise 1: LSTM Digital Twin
Exercise 2: LSTM Emulates MIMO MPC
Model Predictive Control (MPC) is applied online with real-time optimizers that coordinate control moves. This case study demonstrates training and replacement of the MPC with an LSTM network. Two prior case studies demonstrate this same approach with PID control and SISO (Single Input, Single Output) MPC. In this case study, the LSTM network is trained from a 2x2 MIMO MPC (Single Input Single Output, Model Predictive Control). LSTM (Long Short Term Memory) networks are a special type of RNN (Recurrent Neural Network) that is structured to remember and predict based on long-term dependencies that are trained with time-series data.

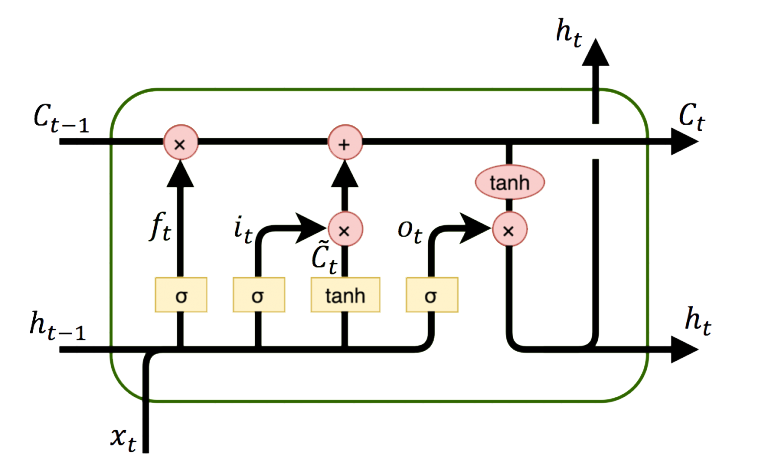
LSTM (Long Short Term Memory) networks are a special type of RNN (Recurrent Neural Network) that is structured to remember and predict based on long-term dependencies that are trained with time-series data. An LSTM repeating module has four interacting components.
LSTM (Long Short Term Memory) networks are a special type of RNN (Recurrent Neural Network) that is structured to remember and predict based on long-term dependencies that are trained with time-series data. An LSTM repeating module has four interacting components.
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/LiBFV7ptm4M" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> (:htmlend:)

(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/EC3QOvgRDSs" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> (:htmlend:)
plt.figure(figsize=(10,5)) plt.plot(train['Time'][window:],Yu,label='LSTM') plt.plot(train['Time'][window:],Ym,label='Measured') plt.plot(train['Q1'],label='heater')
plt.figure(figsize=(10,6)) plt.subplot(2,1,1) plt.plot(train['Time'][window:],Yu,'r-',label='LSTM') plt.plot(train['Time'][window:],Ym,'k--',label='Measured') plt.ylabel('Temperature (°C)')
plt.xlabel('Time (sec)'); plt.ylabel('Values')
plt.subplot(2,1,2) plt.plot(train['Q1'],label='heater (%)') plt.legend() plt.xlabel('Time (sec)'); plt.ylabel('Heater')
plt.figure(figsize=(10,5))
plt.figure(figsize=(10,6))
plt.figure(figsize=(10,5))
plt.figure(figsize=(10,6))
plt.xlabel('Time (sec)'); ylabel('Values')
plt.xlabel('Time (sec)'); plt.ylabel('Values')
Develop a model of the dynamic temperature response of the TCLab and compare the LSTM model prediction to a second-order linear differential equation solution. Use the 4 hours of dynamic data from a TCLab (14400 data points = 1 second sample rate for 4 hours) or else generate new data (840 data points = 1 second sample rate for 14 min).
(:toggle hide tclab_data button show="Generate New TCLab Data":)
Develop a model of the dynamic temperature response of the TCLab and compare the LSTM model prediction to a second-order linear differential equation solution. Use the 4 hours of dynamic data from a TCLab (14400 data points = 1 second sample rate for 4 hours) for training and generate new data (840 data points = 1 second sample rate for 14 min) for validation (see sample validation data).
(:toggle hide tclab_data button show="Generate New TCLab Data for Validation":)
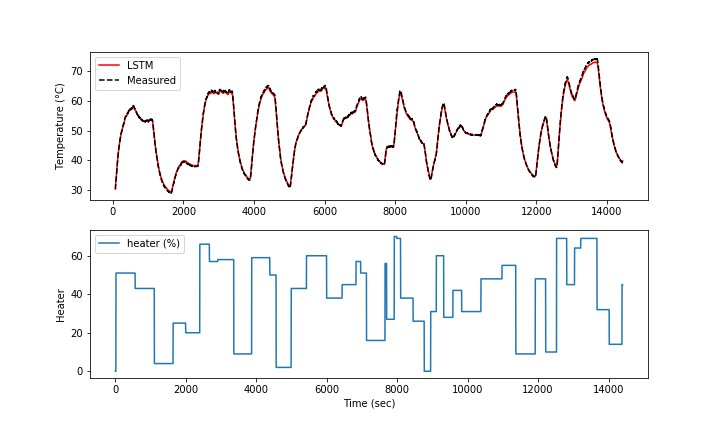
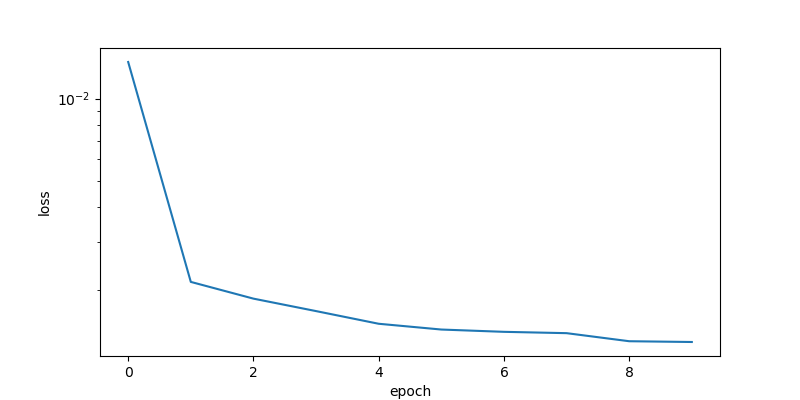
The LSTM model is trained with the TCLab 4 hours data set for 10 epochs. The loss function decreases for the first few epochs and then does not significantly change after that.
The model predictions have good agreement with the measurements. The next steps are to perform validation to determine the predictive capability of the model on a different data set.
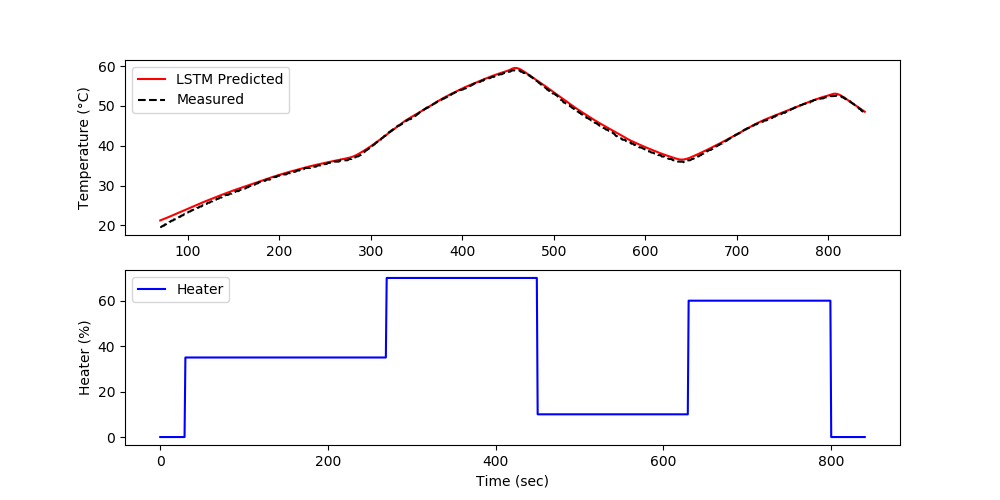
The validation shows the performance on data that was not used in the training. In this case, a separate data file is generated versus splitting the training and test data.
The forecast is generated by using the prior LSTM predictions to predict future temperatures. The measurements are only used for initializing the predictions and then predictions are used to predict following values.
- Load historic values of length 'window' and next real value for model
- Each time step uses last 'window' number of changes to predict the next change
- Each time step uses last 'window' to predict the next change
model.add(LSTM(units=50, return_sequences=True, input_shape=(X.shape[1],X.shape[2])))
model.add(LSTM(units=50, return_sequences=True, input_shape=(X.shape[1],X.shape[2])))
model.compile(optimizer = 'adam', loss = 'mean_squared_error', metrics = ['accuracy'])
model.compile(optimizer = 'adam', loss = 'mean_squared_error', metrics = ['accuracy'])
plt.xlabel('epoch'); plt.ylabel('loss')
plt.legend() plt.xlabel('Time (sec)'); ylabel('Values')
plt.show() (:sourceend:)

TCLab LSTM Validation

(:source lang=python:)
- Load model
(:sourceend:)
TCLab LSTM Forecast
The forecast is generated by using the prior LSTM predictions to predict future temperatures. The measurements are only used for initializing the predictions and then predictions are used to predict following values.

(:source lang=python:)
%matplotlib inline
import time
Develop a model of the dynamic temperature response of the TCLab and compare the LSTM model prediction to a second-order linear differential equation solution. Use the prior temperature values and heater values to predict the next temperature value. Show the model validation that predicts based on prior data as well as a forecast assessment where measurements are not used to generate the predictions.
(:toggle hide lstm button show="Show LSTM Solution":) (:div id=lstm:)
Solution with LSTM Model
Develop a model of the dynamic temperature response of the TCLab and compare the LSTM model prediction to a second-order linear differential equation solution. Use the 4 hours of dynamic data from a TCLab (14400 data points = 1 second sample rate for 4 hours) or else generate new data (840 data points = 1 second sample rate for 14 min).
(:toggle hide tclab_data button show="Generate New TCLab Data":) (:div id=tclab_data:)
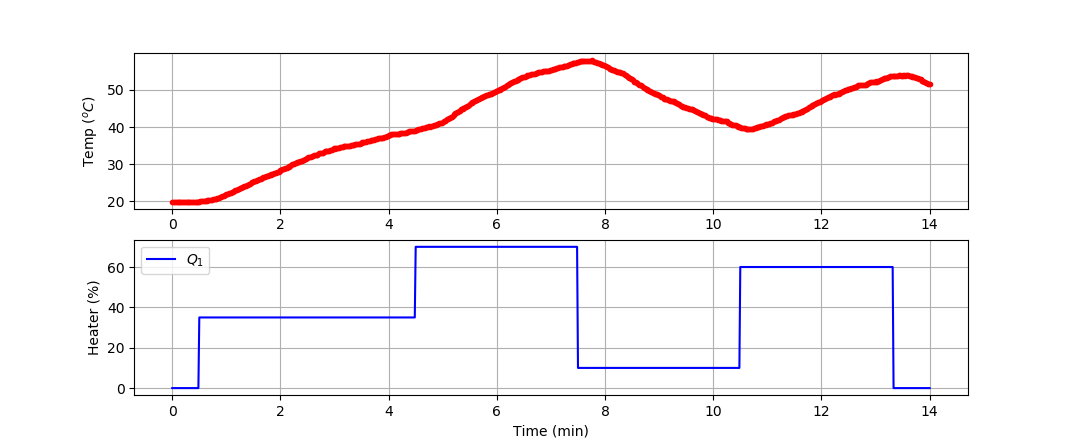
- generate new data
import numpy as np import matplotlib.pyplot as plt import pandas as pd import tclab import time
n = 840 # Number of second time points (14 min) tm = np.linspace(0,n,n+1) # Time values lab = tclab.TCLab() T1 = [lab.T1] T2 = [lab.T2] Q1 = np.zeros(n+1) Q2 = np.zeros(n+1) Q1[30:] = 35.0 Q1[270:] = 70.0 Q1[450:] = 10.0 Q1[630:] = 60.0 Q1[800:] = 0.0 for i in range(n):
lab.Q1(Q1[i])
lab.Q2(Q2[i])
time.sleep(1)
print(Q1[i],lab.T1)
T1.append(lab.T1)
T2.append(lab.T2)
lab.close()
- Save data file
data = np.vstack((tm,Q1,Q2,T1,T2)).T np.savetxt('tclab_data.csv',data,delimiter=',', header='Time,Q1,Q2,T1,T2',comments='')
- Create Figure
plt.figure(figsize=(10,7)) ax = plt.subplot(2,1,1) ax.grid() plt.plot(tm/60.0,T1,'r.',label=r'$T_1$') plt.ylabel(r'Temp ($^oC$)') ax = plt.subplot(2,1,2) ax.grid() plt.plot(tm/60.0,Q1,'b-',label=r'$Q_1$') plt.ylabel(r'Heater (%)') plt.xlabel('Time (min)') plt.legend() plt.savefig('tclab_data.png') plt.show() (:sourceend:) (:divend:)
Use the measured temperature and heater values to predict the next temperature value with an LSTM model. Validate the model with a new data set in a predictive and forecast mode. The predictive mode predicts one step ahead while the forecast does not use temperature measurements to generate the predictions.
(:toggle hide lstm button show="Show LSTM Solution":) (:div id=lstm:)
Solution with LSTM Model
(:source lang=python:) import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline from sklearn.preprocessing import MinMaxScaler
- For LSTM model
from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM from keras.layers import Dropout from keras.callbacks import EarlyStopping from keras.models import load_model
- Load training data
file = 'https://apmonitor.com/do/uploads/Main/tclab_dyn_data3.txt' train = pd.read_csv(file)
- Scale features
s1 = MinMaxScaler(feature_range=(-1,1)) Xs = s1.fit_transform(train'T1','Q1'?)
- Scale predicted value
s2 = MinMaxScaler(feature_range=(-1,1)) Ys = s2.fit_transform(train'T1'?)
- Load historic values of length 'window' and next real value for model
- Each time step uses last 'window' number of changes to predict the next change
window = 70 X = [] Y = [] for i in range(window,len(Xs)):
X.append(Xs[i-window:i,:])
Y.append(Ys[i])
- Reshape data to format accepted by LSTM
X, Y = np.array(X), np.array(Y)
- create and train LSTM model
- Initialize LSTM model
model = Sequential()
model.add(LSTM(units=50, return_sequences=True, input_shape=(X.shape[1],X.shape[2]))) model.add(Dropout(0.2)) model.add(LSTM(units=50, return_sequences=True)) model.add(Dropout(0.2)) model.add(LSTM(units=50)) model.add(Dropout(0.2)) model.add(Dense(units=1)) model.compile(optimizer = 'adam', loss = 'mean_squared_error', metrics = ['accuracy'])
- Allow for early exit
es = EarlyStopping(monitor='loss',mode='min',verbose=1,patience=10)
- Fit (and time) LSTM model
t0 = time.time() history = model.fit(X, Y, epochs = 10, batch_size = 250, callbacks=[es], verbose=1) t1 = time.time() print('Runtime: %.2f s' %(t1-t0))
- Plot loss
plt.figure(figsize=(8,4)) plt.semilogy(history.history['loss']) plt.savefig('tclab_loss.png') model.save('model.h5')
- Verify the fit of the model
Yp = model.predict(X)
- un-scale outputs
Yu = s2.inverse_transform(Yp) Ym = s2.inverse_transform(Y)
plt.figure(figsize=(10,5)) plt.plot(train['Time'][window:],Yu,label='LSTM') plt.plot(train['Time'][window:],Ym,label='Measured') plt.plot(train['Q1'],label='heater') plt.savefig('tclab_fit.png') plt.show() (:sourceend:)

TCLab LSTM Validation

(:source lang=python:) v = load_model('model.h5')
- Load training data
test = pd.read_csv('https://apmonitor.com/pdc/uploads/Main/tclab_data4.txt')
Xt = test'T1','Q1'?.values Yt = test'T1'?.values
Xts = s1.transform(Xt) Yts = s2.transform(Yt)
Xti = [] Yti = [] for i in range(window,len(Xts)):
Xti.append(Xts[i-window:i,:])
Yti.append(Yts[i])
- Reshape data to format accepted by LSTM
Xti, Yti = np.array(Xti), np.array(Yti)
- Verify the fit of the model
Ytp = model.predict(Xti)
- un-scale outputs
Ytu = s2.inverse_transform(Ytp) Ytm = s2.inverse_transform(Yti)
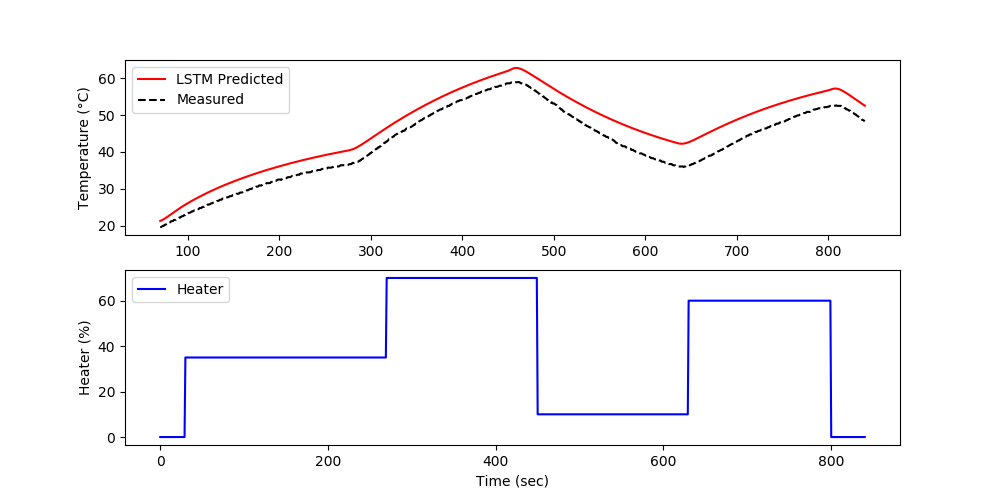
plt.figure(figsize=(10,5)) plt.subplot(2,1,1) plt.plot(test['Time'][window:],Ytu,'r-',label='LSTM Predicted') plt.plot(test['Time'][window:],Ytm,'k--',label='Measured') plt.legend() plt.ylabel('Temperature (°C)') plt.subplot(2,1,2) plt.plot(test['Time'],test['Q1'],'b-',label='Heater') plt.xlabel('Time (sec)'); plt.ylabel('Heater (%)') plt.legend() plt.savefig('tclab_validate.png') (:sourceend:)
TCLab LSTM Forecast
The forecast is generated by using the prior LSTM predictions to predict future temperatures. The measurements are only used for initializing the predictions and then predictions are used to predict following values.

(:source lang=python:)
- Using predicted values to predict next step
Xtsq = Xts.copy() for i in range(window,len(Xtsq)):
Xin = Xtsq[i-window:i].reshape((1, window, 2))
Xtsq[i][0] = v.predict(Xin)
Yti[i-window] = Xtsq[i][0]
- Ytu = (Yti - s2.min_[0])/s2.scale_[0]
Ytu = s2.inverse_transform(Yti)
plt.figure(figsize=(10,5)) plt.subplot(2,1,1) plt.plot(test['Time'][window:],Ytu,'r-',label='LSTM Predicted') plt.plot(test['Time'][window:],Ytm,'k--',label='Measured') plt.legend() plt.ylabel('Temperature (°C)') plt.subplot(2,1,2) plt.plot(test['Time'],test['Q1'],'b-',label='Heater') plt.xlabel('Time (sec)'); plt.ylabel('Heater (%)') plt.legend() plt.savefig('tclab_forecast.png') plt.show()
Solution with LSTM Model
Solution with 2nd-Order Model
$$\min \sum_{i=1}^{n} \left(T_{C1,meas}-T_{C1,pred}\right)^2$$
$$\min \sum_{i=1}^{n} \left(T_{C1,meas,i}-T_{C1,pred,i}\right)^2$$
$$\tau_2 \frac{dT_{C1}}{dt} + \left(T_{C1}\right) = T_{H1}$$
$$\tau_2 \frac{dT_{C1}}{dt} + T_{C1} = T_{H1}$$
{$\min \sum_{i=1}^{n} \left(T_{C1,meas}-T_{C1,pred}\right)^2
$$\min \sum_{i=1}^{n} \left(T_{C1,meas}-T_{C1,pred}\right)^2$$
A second order model is aligned with data by adjusting unknown parameters `K_1`, `\tau_1`, and `\tau_2` to minimize the sum of squared errors.
A second order model is aligned with data by adjusting unknown parameters to minimize the sum of squared errors. The adjusted parameters are `K_1`, `\tau_1`, and `\tau_2`.
{$\min \sum_{i=1}^{n} \left(T_{C1,meas}-T_{C1,pred}\right)^2
(:toggle hide lstm button show="Show LSTM Keras TCLab Code":)
(:toggle hide lstm button show="Show LSTM Solution":)
(:sourceend:) (:divend:)
(:toggle hide second_order button show="Show 2nd-Order Solution":) (:div id=second_order:)
A second order model is aligned with data by adjusting unknown parameters `K_1`, `\tau_1`, and `\tau_2` to minimize the sum of squared errors.
$$\tau_1 \frac{dT_{H1}}{dt} + \left(T_{H1}-T_a\right) = K_1 \, Q_1$$
$$\tau_2 \frac{dT_{C1}}{dt} + \left(T_{C1}\right) = T_{H1}$$
The first 3000 data points train the model and the next 6000 data points validate the model predictions on data that has not been used for training.
Training 2nd-Order Model
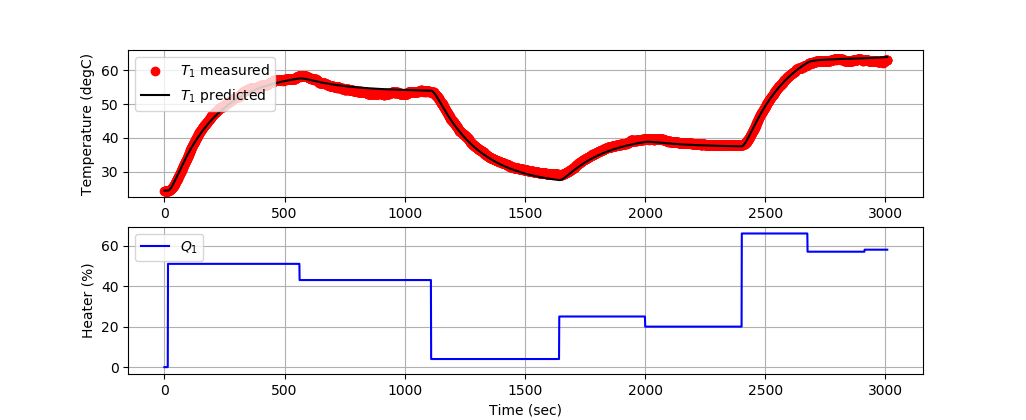
Validating 2nd-Order Model
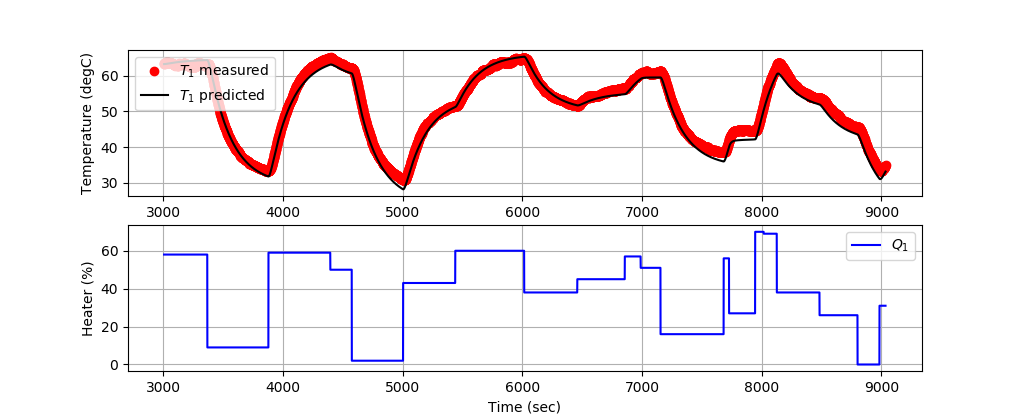
(:source lang=python:) import numpy as np import matplotlib.pyplot as plt from gekko import GEKKO import pandas as pd
file = 'https://apmonitor.com/do/uploads/Main/tclab_dyn_data3.txt' data = pd.read_csv(file)
- subset for training
n = 3000 tm = data['Time'][0:n].values Q1s = data['Q1'][0:n].values T1s = data['T1'][0:n].values
m = GEKKO() m.time = tm
- Parameters to Estimate
K1 = m.FV(value=0.5,lb=0.1,ub=1.0) tau1 = m.FV(value=150,lb=50,ub=250) tau2 = m.FV(value=15,lb=10,ub=20) K1.STATUS = 1 tau1.STATUS = 1 tau2.STATUS = 1
- Model Inputs
Q1 = m.Param(value=Q1s) Ta = m.Param(value=23.0) # degC T1m = m.Param(T1s)
- Model Variables
TH1 = m.Var(value=T1s[0]) TC1 = m.Var(value=T1s)
- Objective Function
m.Minimize((T1m-TC1)**2)
- Equations
m.Equation(tau1 * TH1.dt() + (TH1-Ta) == K1*Q1) m.Equation(tau2 * TC1.dt() + TC1 == TH1)
- Global Options
m.options.IMODE = 5 # MHE m.options.EV_TYPE = 2 # Objective type m.options.NODES = 2 # Collocation nodes m.options.SOLVER = 3 # IPOPT
- Predict Parameters and Temperatures
m.solve()
- Create plot
plt.figure(figsize=(10,7))
ax=plt.subplot(2,1,1) ax.grid() plt.plot(tm,T1s,'ro',label=r'$T_1$ measured') plt.plot(tm,TC1.value,'k-',label=r'$T_1$ predicted') plt.ylabel('Temperature (degC)') plt.legend(loc=2) ax=plt.subplot(2,1,2) ax.grid() plt.plot(tm,Q1s,'b-',label=r'$Q_1$') plt.ylabel('Heater (%)') plt.xlabel('Time (sec)') plt.legend(loc='best')
- Print optimal values
print('K1: ' + str(K1.newval)) print('tau1: ' + str(tau1.newval)) print('tau2: ' + str(tau2.newval))
- Save and show figure
plt.savefig('tclab_2nd_order_fit.png')
- Validation
tm = data['Time'][n:3*n].values Q1s = data['Q1'][n:3*n].values T1s = data['T1'][n:3*n].values
v = GEKKO() v.time = tm
- Parameters to Estimate
K1 = K1.newval tau1 = tau1.newval tau2 = tau2.newval Q1 = v.Param(value=Q1s) Ta = v.Param(value=23.0) # degC TH1 = v.Var(value=T1s[0]) TC1 = v.Var(value=T1s[0]) v.Equation(tau1 * TH1.dt() + (TH1-Ta) == K1*Q1) v.Equation(tau2 * TC1.dt() + TC1 == TH1) v.options.IMODE = 4 # Simulate v.options.NODES = 2 # Collocation nodes v.options.SOLVER = 1
- Predict Parameters and Temperatures
v.solve(disp=True)
- Create plot
plt.figure(figsize=(10,7))
ax=plt.subplot(2,1,1) ax.grid() plt.plot(tm,T1s,'ro',label=r'$T_1$ measured') plt.plot(tm,TC1.value,'k-',label=r'$T_1$ predicted') plt.ylabel('Temperature (degC)') plt.legend(loc=2) ax=plt.subplot(2,1,2) ax.grid() plt.plot(tm,Q1s,'b-',label=r'$Q_1$') plt.ylabel('Heater (%)') plt.xlabel('Time (sec)') plt.legend(loc='best')
- Save and show figure
plt.savefig('tclab_2nd_order_validate.png') plt.show()
(:toggle hide keras button show="Show All Keras Example Code":)
(:toggle hide keras button show="Show Sine Keras Example Code":)
(:toggle hide gekko button show="Show Python Source":) (:div id=gekko:)
(:toggle hide lstm button show="Show LSTM Keras TCLab Code":) (:div id=lstm:)
Develop a model of the dynamic temperature response of the TCLab and compare the LSTM model prediction to a second-order linear differential equation solution. Use the prior temperature values and heater values to predict the next temperature value. Show the model validation that predicts based on prior data as well as a predictive assessment where measurements are not used to generate the predictions.
Develop a model of the dynamic temperature response of the TCLab and compare the LSTM model prediction to a second-order linear differential equation solution. Use the prior temperature values and heater values to predict the next temperature value. Show the model validation that predicts based on prior data as well as a forecast assessment where measurements are not used to generate the predictions.
LSTM Model Validation
LSTM Prediction Validation
When performing the validation it is also important to determine how the model performs with without measurements when it uses prior predictions (not measurements) to predict the next outcome. This is important to determine how well the model performs in a predictive application such as model predictive control where the model is projected forward minutes to hours to determine the sequence of optimal manipulated variable moves and possible future constraint violation.
LSTM Forecast Validation
When performing the validation it is also important to determine how the model performs with without measurements when it uses prior predictions to predict the next outcome. This is important to determine how well the model performs in a predictive application such as model predictive control where the model is projected forward over the control horizon to determine the sequence of optimal manipulated variable moves and possible future constraint violation. Generating predictions without measurement feedback is a forecast.
Repeat the above exercise with the TCLab and compare the LSTM model prediction to a second order linear differential equation model. Use the prior temperature values and heater values to predict the next temperature value. Show the model validation with one-step forward as well as a predictive assessment where measurements are not used to generate the predictions.
Develop a model of the dynamic temperature response of the TCLab and compare the LSTM model prediction to a second-order linear differential equation solution. Use the prior temperature values and heater values to predict the next temperature value. Show the model validation that predicts based on prior data as well as a predictive assessment where measurements are not used to generate the predictions.
The LSTM is trained (parameters adjusted) with an input window of prior data and minimized difference between the predicted and next measured value. Sequential methods predict just one next value based on the window of prior data. When there is contextual data (before and after) the desired prediction point, a Convolutional Neural Networks (CNN) may improve performance with fewer resources to train and deploy the network.
The LSTM is trained (parameters adjusted) with an input window of prior data and minimized difference between the predicted and next measured value. Sequential methods predict just one next value based on the window of prior data. When there is contextual data (before and after) the desired prediction point, a Convolutional Neural Network (CNN) may improve performance with fewer resources to train and deploy the network.
(:toggle hide gekko button show="Show Python Gekko Source":)
(:toggle hide gekko button show="Show Python Source":)
The LSTM is trained (parameters adjusted) with an input window of prior data and minimized difference between the predicted and next measured value. Sequential methods predict just one next value based on the window of prior data.
The LSTM is trained (parameters adjusted) with an input window of prior data and minimized difference between the predicted and next measured value. Sequential methods predict just one next value based on the window of prior data. When there is contextual data (before and after) the desired prediction point, a Convolutional Neural Networks (CNN) may improve performance with fewer resources to train and deploy the network.
(:html:) <video controls autoplay loop>
<source src="/do/uploads/Main/lstm_tutorial.mp4" type="video/mp4"> Your browser does not support the video tag.
</video> (:htmlend:)
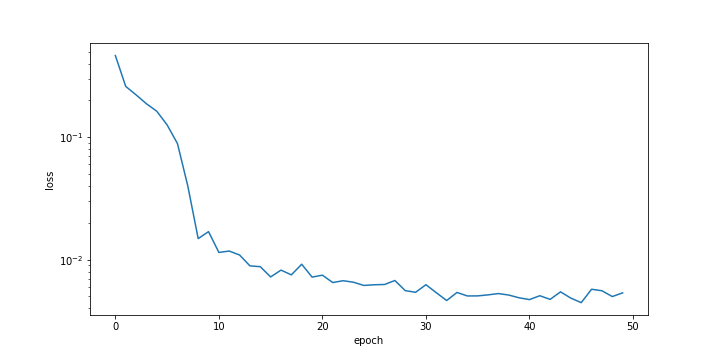

lstm_sine_loss.png

lstm_sine_fit.png
lstm_sine_pred1.png
lstm_sine_pred2.png
lstm_tutorial.mp4
(:title LSTM Networks:) (:keywords sequential processing, artificial intelligence, machine learning, tutorial, tensorflow, keras, gekko:) (:description Long-Short Term Memory (LSTM), Recurrent Neural Networks, and other sequential processing methods consider a window of data to make a future prediction.:)
LSTM (Long Short Term Memory) networks are a special type of RNN (Recurrent Neural Network) that is structured to remember and predict based on long-term dependencies that are trained with time-series data. An LSTM repeating module has four interacting components.

The LSTM is trained (parameters adjusted) with an input window of prior data and minimized difference between the predicted and next measured value. Sequential methods predict just one next value based on the window of prior data.
Data Preparation
Data preparation for LSTM networks involves consolidation, cleansing, separating the input window and output, scaling, and data division for training and validation.
- Consolidation - consolidation is the process of combining disparate data (Excel spreadsheet, PDF report, database, cloud storage) into a single repository.
- Data Cleansing - bad data should be removed and may include outliers, missing entries, failed sensors, or other types of missing or corrupted information.
- Inputs and Outputs - data is separated into inputs (prior time-series window) and outputs (predicted next value). The inputs are fed into a series of functions to produce the output prediction. The squared difference between the predicted output and the measured output is a typical loss (objective) function for fitting.
- Scaling - scaling all data (inputs and outputs) to a range of 0-1 can improve the training process.
- Training and Validation - data is divided into training (e.g. 80%) and validation (e.g. 20%) sets so that the model fit can be evaluated independently of the training. Cross-validation is an approach to divide the training data into multiple sets that are fit separately. The parameter consistency is compared between the multiple models.
lstm_tutorial.mp4
(:html:) <video controls autoplay loop>
<source src="/do/uploads/Main/lstm_tutorial.mp4" type="video/mp4"> Your browser does not support the video tag.
</video> (:htmlend:)
Data Generation and Preparation
(:source lang=python:) import numpy as np import matplotlib.pyplot as plt
- Generate data
n = 500 t = np.linspace(0,20.0*np.pi,n) X = np.sin(t) # X is already between -1 and 1, scaling normally needed (:sourceend:)
Once the data is created, it is converted to a form that can be used by Keras and Tensorflow for training and prediction.
(:source lang=python:)
- Set window of past points for LSTM model
window = 10
- Split 80/20 into train/test data
last = int(n/5.0) Xtrain = X[:-last] Xtest = X[-last-window:]
- Store window number of points as a sequence
xin = [] next_X = [] for i in range(window,len(Xtrain)):
xin.append(Xtrain[i-window:i])
next_X.append(Xtrain[i])
- Reshape data to format for LSTM
xin, next_X = np.array(xin), np.array(next_X) xin = xin.reshape(xin.shape[0], xin.shape[1], 1) (:sourceend:)
LSTM Model Build
An LSTM network relates the input data window to outputs with layers. Instead of just one layer, LSTMs often have multiple layers.
lstm_sine_loss.png
(:source lang=python:) from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM from keras.layers import Dropout
- Initialize LSTM model
m = Sequential() m.add(LSTM(units=50, return_sequences=True, input_shape=(xin.shape[1],1))) m.add(Dropout(0.2)) m.add(LSTM(units=50)) m.add(Dropout(0.2)) m.add(Dense(units=1)) m.compile(optimizer = 'adam', loss = 'mean_squared_error') (:sourceend:)
LSTM Model Training
lstm_sine_fit.png
(:source lang=python:)
- Fit LSTM model
history = m.fit(xin, next_X, epochs = 50, batch_size = 50,verbose=0)
plt.figure() plt.ylabel('loss'); plt.xlabel('epoch') plt.semilogy(history.history['loss']) (:sourceend:)
LSTM Model Validation
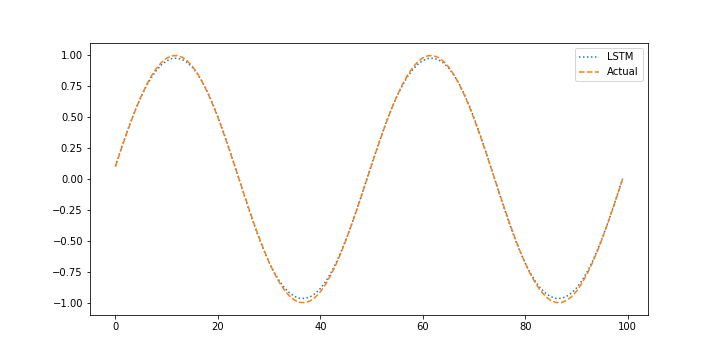
The validation test set assesses the ability of the neural network to predict based on new conditions that were not part of the training set. The validation is performed with the last 20% of the data that was separated from the beginning 80% of data.
lstm_sine_pred1.png
(:source lang=python:)
- Store "window" points as a sequence
xin = [] next_X1 = [] for i in range(window,len(Xtest)):
xin.append(Xtest[i-window:i])
next_X1.append(Xtest[i])
- Reshape data to format for LSTM
xin, next_X1 = np.array(xin), np.array(next_X1) xin = xin.reshape((xin.shape[0], xin.shape[1], 1))
- Predict the next value (1 step ahead)
X_pred = m.predict(xin)
- Plot prediction vs actual for test data
plt.figure() plt.plot(X_pred,':',label='LSTM') plt.plot(next_X1,,label='Actual') plt.legend() (:sourceend:)
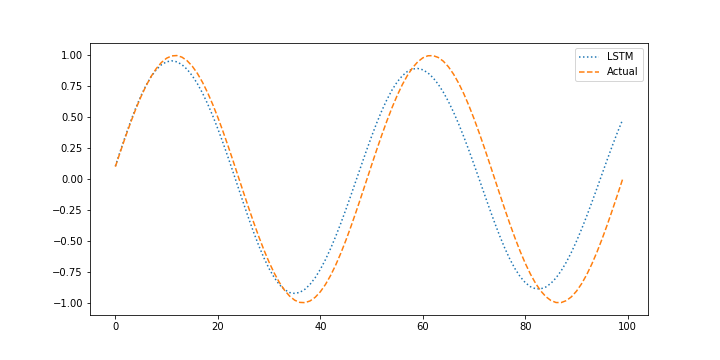
When performing the validation it is also important to determine how the model performs with without measurements when it uses prior predictions (not measurements) to predict the next outcome. This is important to determine how well the model performs in a predictive application such as model predictive control where the model is projected forward minutes to hours to determine the sequence of optimal manipulated variable moves and possible future constraint violation.
lstm_sine_pred2.png
(:source lang=python:)
- Using predicted values to predict next step
X_pred = Xtest.copy() for i in range(window,len(X_pred)):
xin = X_pred[i-window:i].reshape((1, window, 1))
X_pred[i] = m.predict(xin)
- Plot prediction vs actual for test data
plt.figure() plt.plot(X_pred[window:],':',label='LSTM') plt.plot(next_X1,,label='Actual') plt.legend() (:sourceend:)
(:toggle hide keras button show="Show All Keras Example Code":) (:div id=keras:) (:source lang=python:) import numpy as np import matplotlib.pyplot as plt from keras.models import Sequential from keras.layers import Dense from keras.layers import LSTM from keras.layers import Dropout
- Generate data
n = 500 t = np.linspace(0,20.0*np.pi,n) X = np.sin(t) # X is already between -1 and 1, scaling normally needed
- Set window of past points for LSTM model
window = 10
- Split 80/20 into train/test data
last = int(n/5.0) Xtrain = X[:-last] Xtest = X[-last-window:]
- Store window number of points as a sequence
xin = [] next_X = [] for i in range(window,len(Xtrain)):
xin.append(Xtrain[i-window:i])
next_X.append(Xtrain[i])
- Reshape data to format for LSTM
xin, next_X = np.array(xin), np.array(next_X) xin = xin.reshape(xin.shape[0], xin.shape[1], 1)
- Initialize LSTM model
m = Sequential() m.add(LSTM(units=50, return_sequences=True, input_shape=(xin.shape[1],1))) m.add(Dropout(0.2)) m.add(LSTM(units=50)) m.add(Dropout(0.2)) m.add(Dense(units=1)) m.compile(optimizer = 'adam', loss = 'mean_squared_error')
- Fit LSTM model
history = m.fit(xin, next_X, epochs = 50, batch_size = 50,verbose=0)
plt.figure() plt.ylabel('loss'); plt.xlabel('epoch') plt.semilogy(history.history['loss'])
- Store "window" points as a sequence
xin = [] next_X1 = [] for i in range(window,len(Xtest)):
xin.append(Xtest[i-window:i])
next_X1.append(Xtest[i])
- Reshape data to format for LSTM
xin, next_X1 = np.array(xin), np.array(next_X1) xin = xin.reshape((xin.shape[0], xin.shape[1], 1))
- Predict the next value (1 step ahead)
X_pred = m.predict(xin)
- Plot prediction vs actual for test data
plt.figure() plt.plot(X_pred,':',label='LSTM') plt.plot(next_X1,,label='Actual') plt.legend()
- Using predicted values to predict next step
X_pred = Xtest.copy() for i in range(window,len(X_pred)):
xin = X_pred[i-window:i].reshape((1, window, 1))
X_pred[i] = m.predict(xin)
- Plot prediction vs actual for test data
plt.figure() plt.plot(X_pred[window:],':',label='LSTM') plt.plot(next_X1,,label='Actual') plt.legend() plt.show() (:sourceend:) (:divend:)
Exercise
Repeat the above exercise with the TCLab and compare the LSTM model prediction to a second order linear differential equation model. Use the prior temperature values and heater values to predict the next temperature value. Show the model validation with one-step forward as well as a predictive assessment where measurements are not used to generate the predictions.
(:toggle hide gekko button show="Show Python Gekko Source":) (:div id=gekko:)
(:source lang=python:)
(:sourceend:) (:divend:)