Dynamic Optimization

plt.xlabel('Distance'); plt.ylabel('u')

(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/QRXSYLuniO4" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> (:htmlend:)

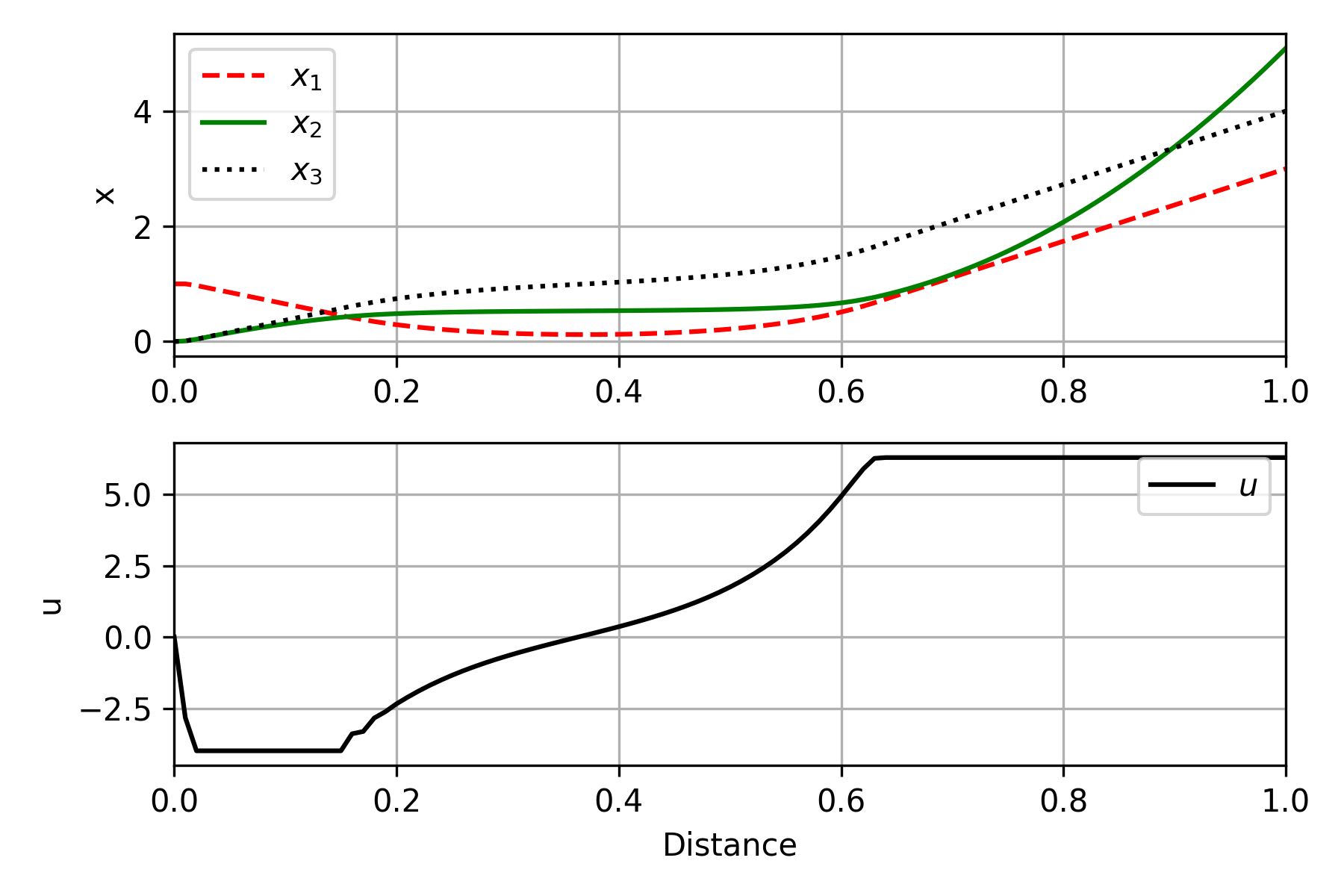
The objective of the hanging chain problem is to find the position of a chain of uniform density and length suspended between two points `a` and `b`. The problem is solved by minimizing the potential energy. This problem is from the COPS benchmark set. The equations are

The Gekko Optimization Suite is a machine learning and optimization package in Python for mixed-integer and differential algebraic equations.

📄 Gekko Publication and References

The GEKKO package is available in Python with pip install gekko. There are additional example problems for equation solving, optimization, regression, dynamic simulation, model predictive control, and machine learning.

(:title Hanging Chain Optimization:) (:keywords optimization, optimal control, benchmark, nonlinear control, dynamic optimization, engineering optimization, Python, GEKKO, differential, algebraic, modeling language:) (:description Hanging chain optimization solved with Python Gekko.:)

The objective of the hanging chain problem is to find the position of a chain of uniform density and length suspendend between two points `a` and `b`. The problem is solved by minimizing the potential energy. This problem is from the COPS benchmark set. The equations are

$$ \begin{array}{llcl} \min_{x, u} & x_2(t_f) \\ \mbox{s.t.} & \dot{x}_1 & = & u \\ & \dot{x}_2 & = & x_1 (1+u^2)^{1/2} \\ & \dot{x}_3 & = & (1+u^2)^{1/2} \\ & x(t_0) &=& (a,0,0)^T \\ & x_1(t_f) &=& b \\ & x_3(t_f) &=& Lp \\ & x(t) &\in& [0,10] \\ & u(t) &\in& [-10,20] \end{array} $$

The parameters of this model are defined as `a=1`, `b=3`, and `Lp=4` with `t` from 0 to 1.

(:toggle hide solution button show="Hanging Chain Source":) (:div id=solution:) (:source lang=python:) from gekko import GEKKO import numpy as np import matplotlib.pyplot as plt

m = GEKKO(remote=False)

n = 101; Lp = 4; b = 3; a = 1

m.time = np.linspace(0,1,n) x1,x2,x3 = m.Array(m.Var,3,lb=0,ub=10) x1.value = a u = m.MV(value=0, lb=-10, ub=20) # integer=True

z = np.zeros(n); z[-1] = 1 final = m.Param(value=z)

m.Equation(x1.dt() == u) m.Equation(x2.dt() == x1 * (1+u**2)**0.5) m.Equation(x3.dt() == (1+u**2)**0.5)

m.Minimize(1000*(x1-b)**2*final) m.Minimize(1000*(x3-Lp)**2*final)

m.options.SOLVER = 3 m.options.NODES = 3 m.options.IMODE = 6 m.Minimize(x2*final)

1. initialize

u.STATUS = 0 m.solve()

1. optimize

m.options.TIME_SHIFT = 0 u.STATUS = 1; u.DCOST = 1e-3 m.solve()

plt.figure(figsize=(6,4)) plt.subplot(2,1,1) plt.plot(m.time,x1.value,'r--',label=r'$x_1$') plt.plot(m.time,x2.value,'g-',label=r'$x_2$') plt.plot(m.time,x3.value,'k:',label=r'$x_3$') plt.ylabel('x'); plt.xlim([0,1]) plt.legend(); plt.grid() plt.subplot(2,1,2) plt.plot(2,1,2) plt.plot(m.time,u.value,'k-',label=r'$u$') plt.grid(); plt.xlim([0,1]); plt.legend() plt.xlabel('Time'); plt.ylabel('u') plt.tight_layout() plt.savefig('chain.png',dpi=300); plt.show() (:sourceend:) (:divend:)

The Gekko Optimization Suite is a machine learning and optimization package in Python for mixed-integer and differential algebraic equations. The GEKKO package is available in Python with pip install gekko. There are additional example problems? for equation solving, optimization, regression, dynamic simulation, model predictive control, and machine learning.