TCLab Simulate Step Response

Objective: Simulate temperature response and compare to data from the TCLab.

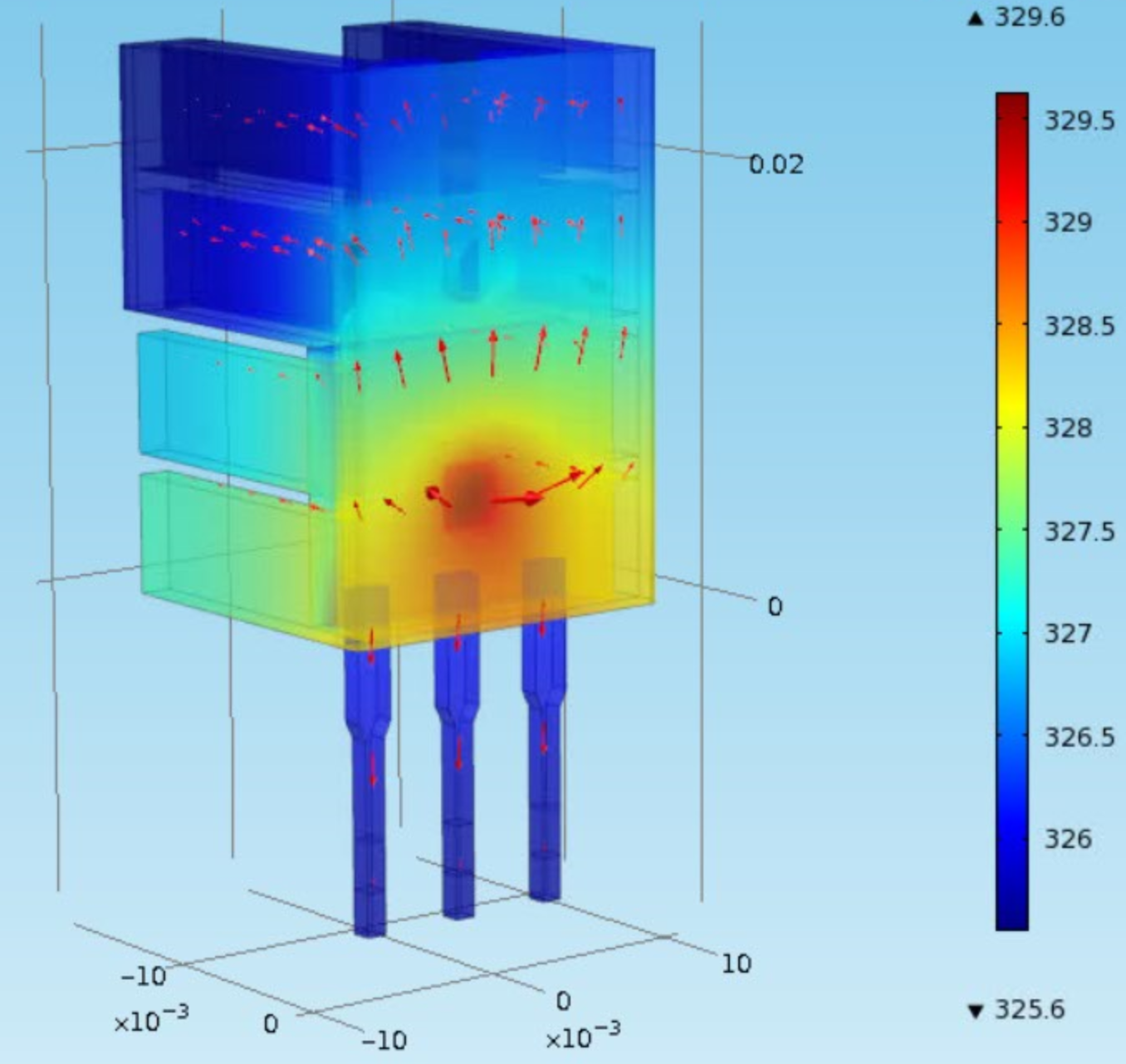A simplified dynamic model of the Temperature Control Lab (TCLab) is the following:

$$\tau_p \frac{dT}{dt} = \left(T_a-T\right) + K_p \, Q$$

With the temperature initially at ambient temperature (`T_a`), simulate the change in temperature over the 5 minutes when heater Q is adjusted to 50%. Use a values of `\tau`=120 sec, `K_p`=0.8oC/%, and `T_a`=23oC. Compare the simulated temperature response to data from the TCLab. Add a simulation prediction to the script below to compare with the TCLab data.

TCLab Step Response

Use the following code to generate a step response or use the TCLab Web Interface.

import numpy as np
import matplotlib.pyplot as plt
import tclab
import time

n = 300  # Number of second time points (5 min)
tm = np.linspace(0,n,n+1) # Time values

# data
lab = tclab.TCLab()
T1 = [lab.T1]
lab.Q1(50)
for i in range(n):
    time.sleep(1)
    print(lab.T1)
    T1.append(lab.T1)
lab.close()

# Plot results
plt.figure(1)
plt.plot(tm,T1,'r.',label='Measured')
plt.ylabel('Temperature (degC)')
plt.xlabel('Time (sec)')
plt.legend()
plt.show()
[$[Get Code]]

Solutions

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
import tclab
import time

n = 300  # Number of second time points (5 min)
tm = np.linspace(0,n,n+1) # Time values

# data
lab = tclab.TCLab()
T1 = [lab.T1]
lab.Q1(50)
for i in range(n):
    time.sleep(1)
    print(lab.T1)
    T1.append(lab.T1)
lab.close()

# simulation
def labsim(TC,t):
    dTCdt = ((23-TC) + 0.8*50)/120.0
    return dTCdt
Tsim = odeint(labsim,23,tm)

# Plot results
plt.figure(1)
plt.plot(tm,Tsim,'b-',label='Simulated')
plt.plot(tm,T1,'r.',label='Measured')
plt.ylabel('Temperature (degC)')
plt.xlabel('Time (sec)')
plt.legend()
plt.show()
[$[Get Code]]

import numpy as np
import matplotlib.pyplot as plt
import tclab
import time
# pip install gekko
from gekko import GEKKO

n = 300  # Number of second time points (5 min)

# data
lab = tclab.TCLab()
T1 = [lab.T1]
lab.Q1(50)
for i in range(n):
    time.sleep(1)
    print(lab.T1)
    T1.append(lab.T1)
lab.close()

# simulation
m = GEKKO()
m.time = np.linspace(0,n,n+1)
TC = m.Var(23)
m.Equation(120*TC.dt()==(23-TC)+0.8*50)
m.options.IMODE = 4 # dynamic simulation
m.solve(disp=False)

# Plot results
plt.figure(1)
plt.plot(m.time,TC,'b-',label='Simulated')
plt.plot(m.time,T1,'r.',label='Measured')
plt.ylabel('Temperature (degC)')
plt.xlabel('Time (sec)')
plt.legend()
plt.show()
[$[Get Code]]
💬