Linearization of Differential Equations
 |  |  |  |
|---|
Linearization is the process of taking the gradient of a nonlinear function with respect to all variables and creating a linear representation at that point. It is required for certain types of analysis such as stability analysis, solution with a Laplace transform, and to put the model into linear state-space form. Consider a nonlinear differential equation model that is derived from balance equations with input u and output y.
$$\frac{dy}{dt} = f(y,u)$$
The right hand side of the equation is linearized by a Taylor series expansion, using only the first two terms.
$$\frac{dy}{dt} = f(y,u) \approx f \left(\bar y, \bar u\right) + \frac{\partial f}{\partial y}\bigg|_{\bar y,\bar u} \left(y-\bar y\right) + \frac{\partial f}{\partial u}\bigg|_{\bar y,\bar u} \left(u-\bar u\right)$$
If the values of `\bar u` and `\bar y` are chosen at steady state conditions then `f(\bar y, \bar u)=0` because the derivative term `{dy}/{du}=0` at steady state. To simplify the final linearized expression, deviation variables are defined as `y' = y-\bar y` and `u' = u - \bar u`. A deviation variable is a change from the nominal steady state conditions. The derivatives of the deviation variable is defined as `{dy'}/{dt} = {dy}/{dt}` because `{d\bar y}/{dt} = 0` in `{dy'}/{dt} = {d(y-\bar y)}/{dt} = {dy}/{dt} - \cancel{{d\bar y}/{dt}}`. If there are additional variables such as a disturbance variable `d` then it is added as another term in deviation variable form `d' = d - \bar d`.
$$\frac{dy'}{dt} = \alpha y' + \beta u' + \gamma d'$$
The values of the constants `\alpha`, `\beta`, and `\gamma` are the partial derivatives of `f(y,u,d)` evaluated at steady state conditions.
$$\alpha = \frac{\partial f}{\partial y}\bigg|_{\bar y,\bar u,\bar d} \quad \quad \beta = \frac{\partial f}{\partial u}\bigg|_{\bar y,\bar u,\bar d} \quad \quad \gamma = \frac{\partial f}{\partial d}\bigg|_{\bar y,\bar u,\bar d}$$
Example
Part A: Linearize the following differential equation with an input value of u=16.
$$\frac{dx}{dt} = -x^2 + \sqrt{u}$$
Part B: Determine the steady state value of x from the input value and simplify the linearized differential equation.
Part C: Simulate a doublet test with the nonlinear and linear models and comment on the suitability of the linear model to represent the original nonlinear equation solution.
Part A Solution: The equation is linearized by taking the partial derivative of the right hand side of the equation for both x and u.
$$\frac{\partial \left(-x^2 + \sqrt{u}\right)}{\partial x} = \alpha = -2 \, x$$
$$\frac{\partial \left(-x^2 + \sqrt{u}\right)}{\partial u} = \beta = \frac{1}{2} \frac{1}{\sqrt{u}}$$
The linearized differential equation that approximates `\frac{dx}{dt}=f(x,u)` is the following:
$$\frac{dx}{dt} = f \left(x_{ss}, u_{ss}\right) + \frac{\partial f}{\partial x}\bigg|_{x_{ss},u_{ss}} \left(x-x_{ss}\right) + \frac{\partial f}{\partial u}\bigg|_{x_{ss},u_{ss}} \left(u-u_{ss}\right)$$
Substituting in the partial derivatives results in the following differential equation:
$$\frac{dx}{dt} = 0 + \left(-2 x_{ss}\right) \left(x-x_{ss}\right) + \left(\frac{1}{2} \frac{1}{\sqrt{u_{ss}}}\right) \left(u-u_{ss}\right)$$
This is further simplified by defining new deviation variables as `x' = x - x_{ss}` and `u' = u - u_{ss}`.
$$\frac{dx'}{dt} = \alpha x' + \beta u'$$
Part B Solution: The steady state values are determined by setting `\frac{dx}{dt}=0` and solving for x.
$$0 = -x_{ss}^2 + \sqrt{u_{ss}}$$
$$x_{ss}^2 = \sqrt{16}$$
$$x_{ss} = 2$$
At steady state conditions, `frac{dx}{dt}=0` so `f (x_{ss}, u_{ss})=0` as well. Plugging in numeric values gives the simplified linear differential equation:
$$\frac{dx}{dt} = -4 \left(x-2\right) + \frac{1}{8} \left(u-16\right)$$
The partial derivatives can also be obtained from Python, either symbolically with SymPy or else numerically with SciPy.
import sympy as sp
sp.init_printing()
# define symbols
x,u = sp.symbols(['x','u'])
# define equation
dxdt = -x**2 + sp.sqrt(u)
print(sp.diff(dxdt,x))
print(sp.diff(dxdt,u))
# numeric solution with Python
import numpy as np
from scipy.misc import derivative
u = 16.0
x = 2.0
def pd_x(x):
dxdt = -x**2 + np.sqrt(u)
return dxdt
def pd_u(u):
dxdt = -x**2 + np.sqrt(u)
return dxdt
print('Approximate Partial Derivatives')
print(derivative(pd_x,x,dx=1e-4))
print(derivative(pd_u,u,dx=1e-4))
print('Exact Partial Derivatives')
print(-2.0*x) # exact d(f(x,u))/dx
print(0.5 / np.sqrt(u)) # exact d(f(x,u))/du
Python program results
-2*x 1/(2*sqrt(u)) Approximate Partial Derivatives -4.0 0.125 Exact Partial Derivatives -4.0 0.125
The nonlinear function for `\frac{dx}{dt}` can also be visualized with a 3D contour map. The choice of steady state conditions `x_{ss}` and `u_{ss}` produces a planar linear model that represents the nonlinear model only at a certain point. The linear model can deviate from the nonlinear model if used further away from the conditions at which the linear model is derived.
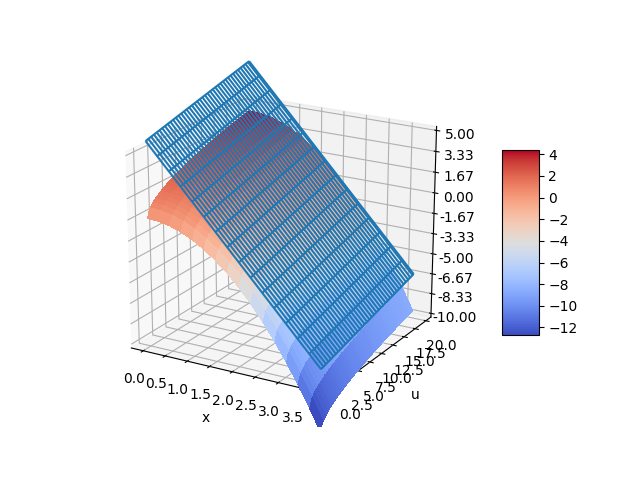
import matplotlib.pyplot as plt
from matplotlib import cm
from matplotlib.ticker import LinearLocator, FormatStrFormatter
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
# Make data.
X = np.arange(0, 4, 0.25)
U = np.arange(0, 20, 0.25)
X, U = np.meshgrid(X, U)
DXDT = -X**2 + np.sqrt(U)
LIN = -4.0 * (X-2.0) + 1.0/8.0 * (U-16.0)
# Plot the surface.
surf = ax.plot_wireframe(X, U, LIN)
surf = ax.plot_surface(X, U, DXDT, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
# Customize the z axis.
ax.set_zlim(-10.0, 5.0)
ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))
# Add a color bar which maps values to colors.
fig.colorbar(surf, shrink=0.5, aspect=5)
# Add labels
plt.xlabel('x')
plt.ylabel('u')
plt.show()
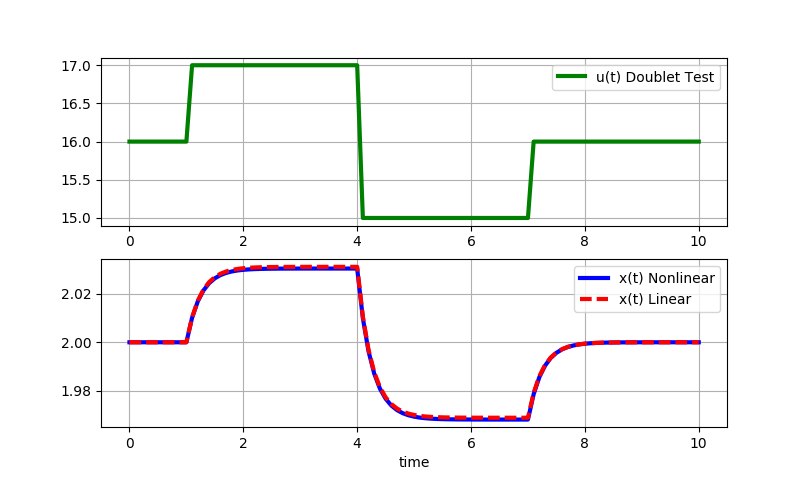
Part C Solution: The final step is to simulate a doublet test with the nonlinear and linear models.
Small step changes (+/-1): Small step changes in u lead to nearly identical responses for the linear and nonlinear solutions. The linearized model is locally accurate.
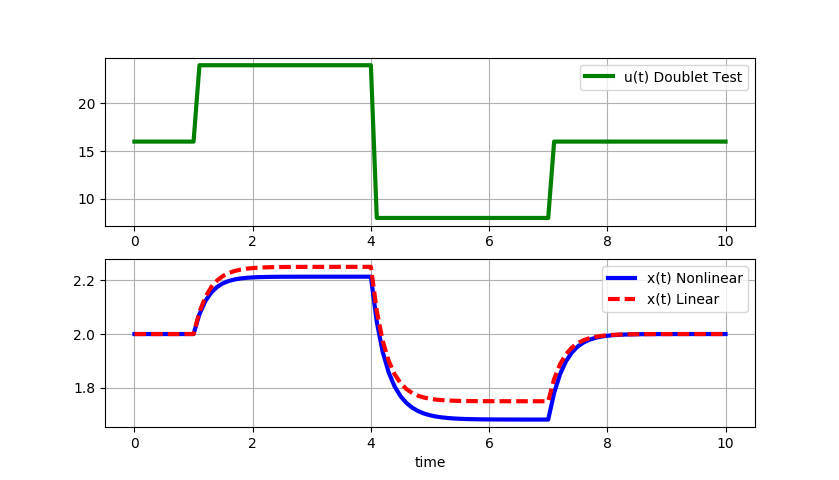
Large step changes (+/-8): As the magnitude of the doublet steps increase, the linear model deviates further from the original nonlinear equation solution.
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# function that returns dz/dt
def model(z,t,u):
x1 = z[0]
x2 = z[1]
dx1dt = -x1**2 + np.sqrt(u)
dx2dt = -4.0*(x2-2.0) + (1.0/8.0)*(u-16.0)
dzdt = [dx1dt,dx2dt]
return dzdt
# steady state conditions
x_ss = 2.0
u_ss = 16.0
# initial condition
z0 = [x_ss,x_ss]
# final time
tf = 10
# number of time points
n = tf * 10 + 1
# time points
t = np.linspace(0,tf,n)
# step input
u = np.ones(n) * u_ss
# magnitude of step
m = 8.0
# change up m at time = 1.0
u[11:] = u[11:] + m
# change down 2*m at time = 4.0
u[41:] = u[41:] - 2.0 * m
# change up m at time = 7.0
u[71:] = u[71:] + m
# store solution
x1 = np.empty_like(t)
x2 = np.empty_like(t)
# record initial conditions
x1[0] = z0[0]
x2[0] = z0[1]
# solve ODE
for i in range(1,n):
# span for next time step
tspan = [t[i-1],t[i]]
# solve for next step
z = odeint(model,z0,tspan,args=(u[i],))
# store solution for plotting
x1[i] = z[1][0]
x2[i] = z[1][1]
# next initial condition
z0 = z[1]
# plot results
plt.figure(1)
plt.subplot(2,1,1)
plt.plot(t,u,'g-',linewidth=3,label='u(t) Doublet Test')
plt.grid()
plt.legend(loc='best')
plt.subplot(2,1,2)
plt.plot(t,x1,'b-',linewidth=3,label='x(t) Nonlinear')
plt.plot(t,x2,'r--',linewidth=3,label='x(t) Linear')
plt.xlabel('time')
plt.grid()
plt.legend(loc='best')
plt.show()