Dynamics and Control

Objective: Quantify the TCLab offset between the setpoint (desired target) and the measured temperature when using a proportional-only controller.

A proportional only (P-only) controller is the simplest implementation of a PID controller without the integral or derivative terms. The controller is an equation that adjusts the controller output, `u(t)`, for input into the system as the manipulated variable. It is a calculation of the difference between the setpoint SP and process variable PV. The adjustable parameter is the controller gain, `K_c`. A large gain produces a controller that reacts aggressively to a difference between the measured PV and target SP.

$$Q(t) = Q_{bias} + K_c \, \left( T_{SP}-T_{PV} \right) = Q_{bias} + K_c \, e(t)$$

The `Q_{bias}` term is a constant that is typically set to the value of `Q(t)` when the controller is first switched from manual to automatic mode. The deviation variable for the heater is the change in value `Q'(t) = Q(t) - Q_{bias}`. For the TCLab, `Q_{bias}`=0 because the TCLab starts with the heater off. The `Q_{bias}` gives bumpless transfer if the error is zero when the controller is turned on. The error from the set point is the difference between the `T_{SP}` and `T_{PV}` and is defined as `e(t) = T_{SP} - T_{PV}`. See additional information on P-only controllers.

The TCLab is a non-integrating process because the temperature returns to ambient conditions when the heater is shut off. A P-only controller has persistent offset between the SP and PV at steady-state for non-integrating systems. The purpose of this assignment is to calculate and then verify the offset for the TCLab.

A common tuning correlation for P-only control is the ITAE (Integral of Time-weighted Absolute Error) method. Use the ITAE setpoint tracking tuning correlation with FOPDT parameters (`K_c`, `\tau_p`, `\theta_p`) determined from the TCLab graphical fitting or TCLab regression exercises.

$$K_c = \frac{0.20}{K_p}\left(\frac{\tau_p}{\theta_p}\right)^{1.22} \quad \mathrm{Set\;point\;tracking}$$

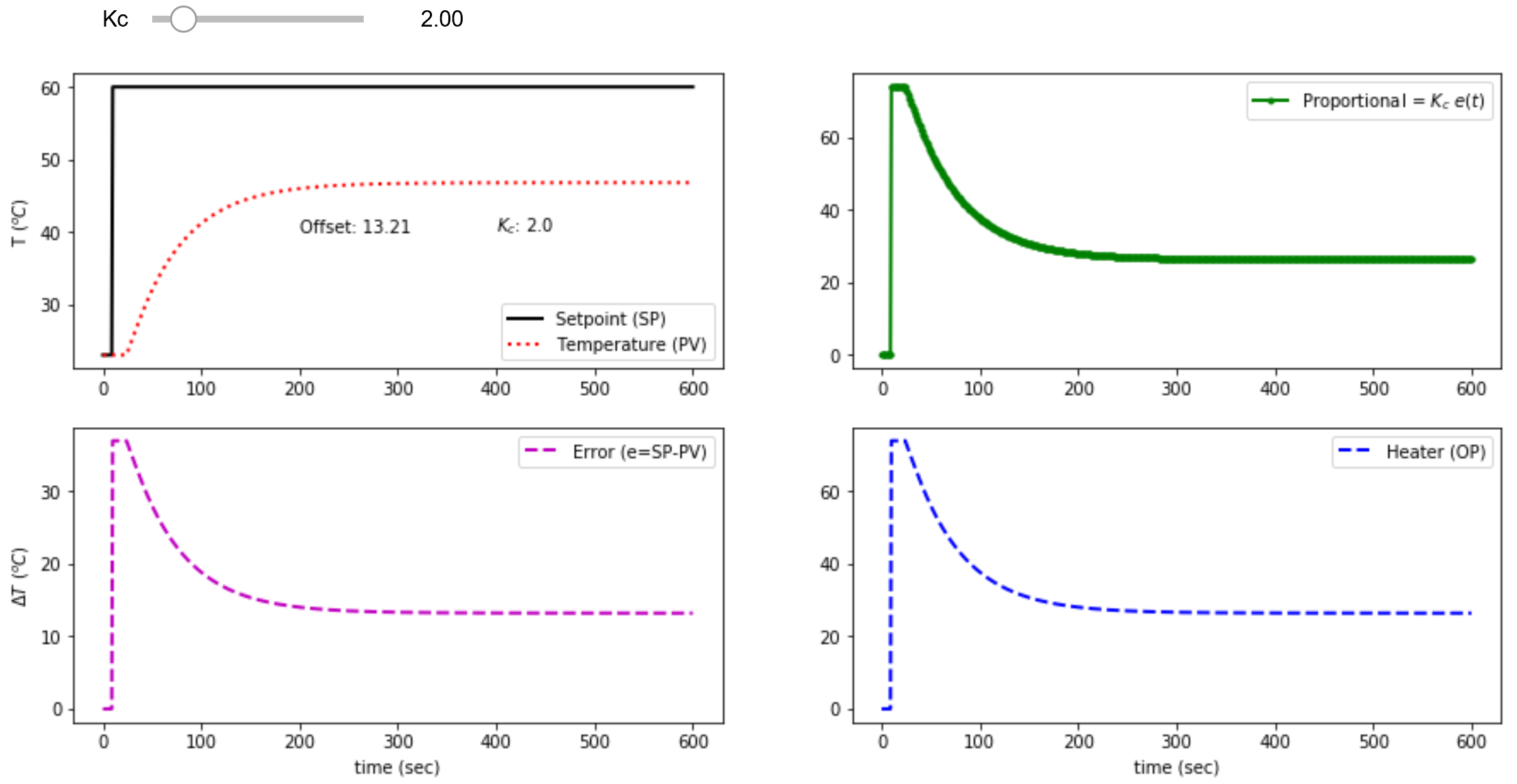
P-Only Offset Simulator

Use the P-Only offset simulator to test the control performance before implementing on the TCLab. The simulator shows the offset for a TCLab FOPDT model with `K_p`=0.9 ^oC/%, `\tau_p`=175.0 sec, and `\theta_p`=15.0 sec. Use the FOPDT model parameters for your own TCLab device for a more accurate estimate of offset. The controller gain `K_c` is adjusted with a slider to compute the updated offset values as shown on the plot.

GitHub Colab

P-Only Control with TCLab

Fill in the value of `K_c` and the P-only equation in the code below and run with the TCLab to experimentally determine the offset from a step in setpoint from 23^oC to 60^oC.

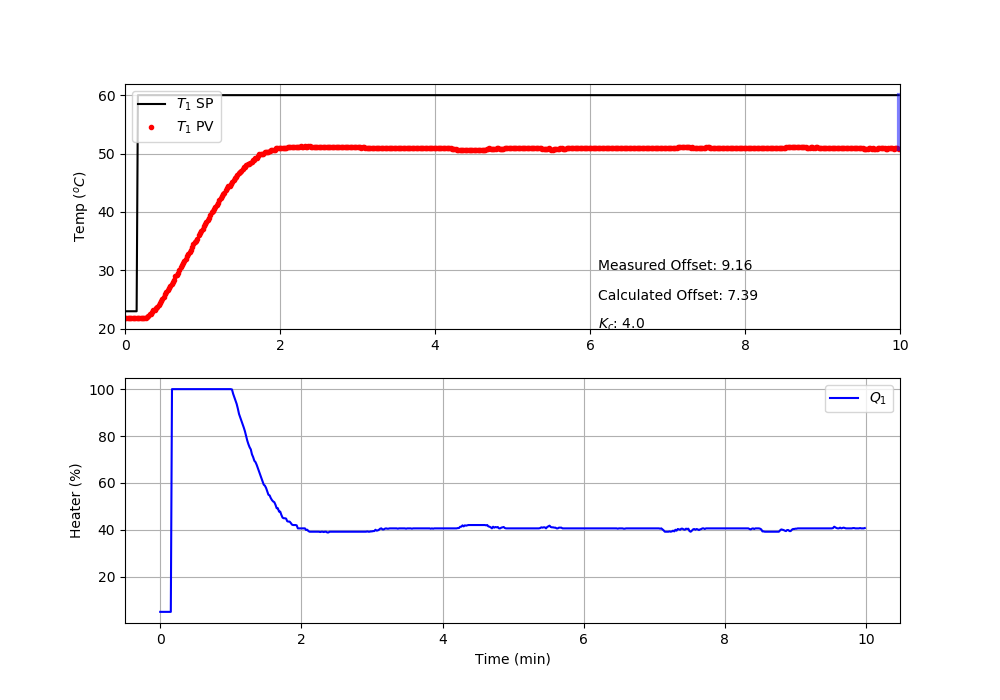
Calculate the predicted offset from the FOPDT model. In the solution, include a plot of the P-only controller response. Indicate the measured and calculated offset values graphically on the plot.

Solution

The predicted offset is calculated from the FOPDT model and P-only controller equation.

$$\tau_p \frac{dT'}{dt} = -T' + K_p \, Q'\left(t-\theta_p\right)$$

At steady-state the model becomes:

$$0 = -(T-23) + K_p \, Q'$$

The control output is:

$$Q' = K_c \left(60-T\right)$$

These two equations are combined to solve for `T`:

$$T=\frac{23+K_p\,K_c\,60}{1+K_p\,K_c}$$

and offset=`(60-T)`:

$$\mathrm{offset} = 60-T = 60 - \frac{23+K_p\,K_c\,60}{1+K_p\,K_c}$$

$$\mathrm{offset} = 60-T = 60 - \frac{23+0.9 \times 4.45 \times 60}{1+0.9 \times 4.45}$$

$$\mathrm{offset} = 60-T = 60 - 52.6 = 7.4^oC$$

The plot of the P-only controller response shows a similar offset (`9.1^oC`) to the calculated value (`7.4^oC`).

import numpy as np
import matplotlib.pyplot as plt
import tclab
import time

# -----------------------------
# Adjust controller gain (Kc)
#  from ITAE tuning correlation
# -----------------------------
Kc = 4.45

n = 600  # Number of second time points (10 min)
tm = np.linspace(0,n-1,n) # Time values
lab = tclab.TCLab()
T1 = np.zeros(n)
Q1 = np.zeros(n)
# step setpoint from 23.0 to 60.0 degC
SP1 = np.ones(n)*23.0
SP1[10:] = 60.0
Q1_bias = 0.0
for i in range(n):
    # record measurement
    T1[i] = lab.T1

    # --------------------------------------------------
    # fill-in P-only controller equation to change Q1[i]
    # --------------------------------------------------
    Q1[i] = Q1_bias + Kc * (SP1[i]-T1[i])

    # implement new heater value
    Q1[i] = max(0,min(100,Q1[i])) # clip to 0-100%
    lab.Q1(Q1[i])
    if i%20==0:
        print(' Heater,   Temp,  Setpoint')
    print(f'{Q1[i]:7.2f},{T1[i]:7.2f},{SP1[i]:7.2f}')
    # wait for 1 sec
    time.sleep(1)
lab.close()
# Save data file
data = np.vstack((tm,Q1,T1,SP1)).T
np.savetxt('P-only.csv',data,delimiter=',',\
           header='Time,Q1,T1,SP1',comments='')

# Create Figure
plt.figure(figsize=(10,7))
ax = plt.subplot(2,1,1)
ax.grid()
plt.plot(tm/60.0,SP1,'k-',label=r'$T_1$ SP')
plt.plot(tm/60.0,T1,'r.',label=r'$T_1$ PV')
plt.text(6.1,30,'Measured Offset: ' + str(np.round(SP1[-1]-T1[-1],2)))
offset = 60 - (23+0.9*Kc*60)/(1+0.9*Kc)
plt.text(6.1,26,'Calculated Offset: ' + str(np.round(offset,2)))
plt.text(6.1,22,r'$K_c$: ' + str(np.round(Kc,2)))  
plt.plot([tm[-1]/60.0,tm[-1]/60.0],[SP1[-1],T1[-1]],\
         'b-',lw=3,alpha=0.5)
plt.ylabel(r'Temp ($^oC$)')
plt.xlim([0,10])
plt.legend(loc=2)
ax = plt.subplot(2,1,2)
ax.grid()
plt.plot(tm/60.0,Q1,'b-',label=r'$Q_1$')
plt.ylabel(r'Heater (%)')
plt.xlabel('Time (min)')
plt.legend(loc=1)
plt.savefig('P-only_Control.png')
plt.show()

[$[Get Code]]