Building Climate Optimization

Climate Control with Dynamic Optimization

Power supplied to buildings comsumes up to 40% of total power generation world-wide. Heating and cooling (climate control) of the buildings is a large part of the building energy consumption. This benchtop experiment simulates optimal climate control by applying principles of modeling, uncertainty analysis, and optimization.

This in-class exercise is a demonstration of dynamic parameter estimation, uncertainty analysis, robust optimization, and dynamic optimization of a simulated climate control system. An Arduino microcontroller board simulates the heating of a small space that has a desired temperature range of 108-112 degF.

The homework assignment on Dynamic Estimation demonstrated how to fit a dynamic model to time-varying data. In this case, the parameters for the gain (K) and time constant (tau) were obtained by minimizing the difference between the model and measured values. Both a sum of squared errors (SSE) and an L1-norm approach were used as objective functions for the optimization problems. In addition, a nonlinear confidence region was obtained to describe the uncertainty in the parameters.

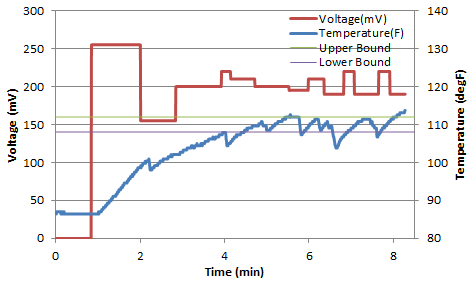
Next, a test was conducted to observe the performance of manual adjustment of the input voltage to maintain the actual temperature within the desired range of 108-112 degF. During this test, another student provided disturbances to the system by intermittently blowing on the transistor and temperature probe. These disturbances represented day-time and night-time factors, varying occupancy, and other changes that could induce a temperature change.

Finally, the dynamic model with optimized parameters was employed to automate the continual optimization of the voltage to maintain the system within the desired temperature range. The description of the parameter confidence levels were also employed to create a robust optimization algorithm that explicitly considers the degree of uncertainty in the solution.

Building the Arduino Temperature Control Module

References

💬