Beam Column Design Optimization
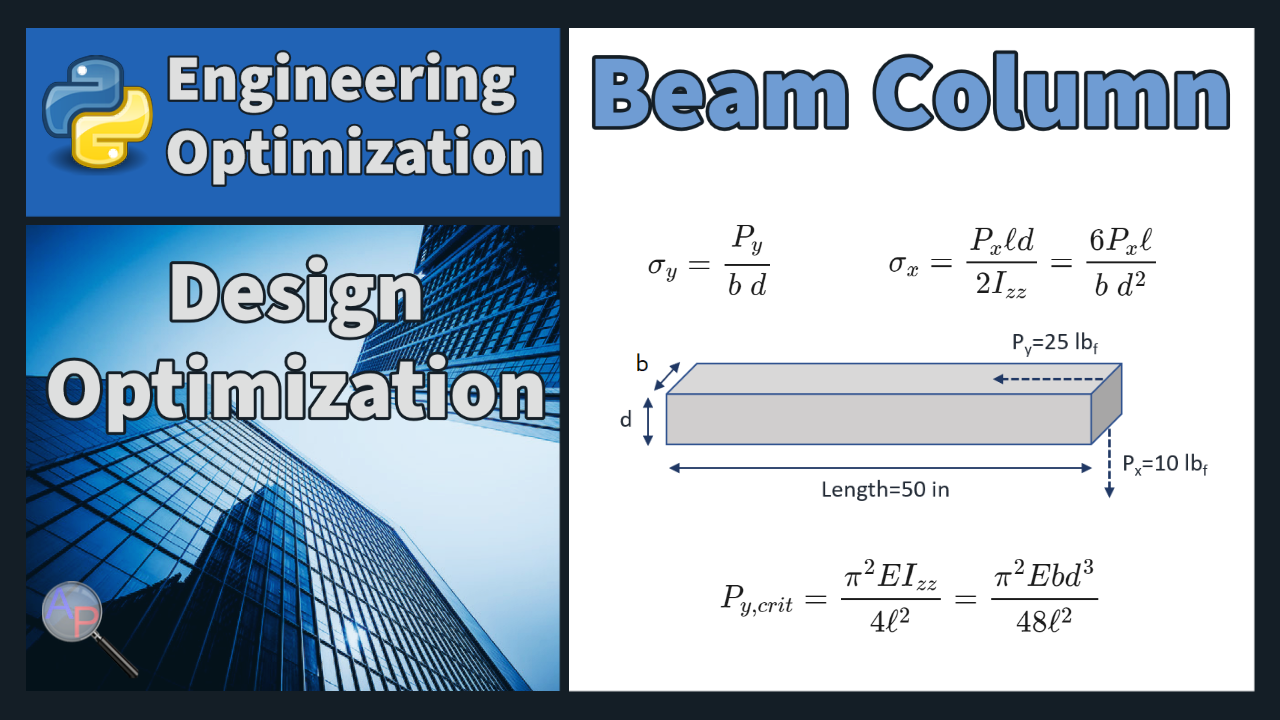
A rectangular beam column is a structural element that combines both the properties of a beam and a column. It has the ability to resist both bending and axial forces. It is typically made up of reinforced concrete, steel or timber and is used in the construction of buildings, bridges and other structures. Optimize a rectangular beam column to carry an axial (horizontal) load of 25 lb and a transverse (vertical) load of 10 lb.
Design the beam column to be minimum weight while staying within the limits of material yield strength and buckling load. Assume that the beam can only bend in the horizontal (y) and vertical (x) directions and there is no bending in the other horizontal (z) dimension. The beam column is made of steel with a density (specific weight) of 0.3 lb/in3, a Young's modulus of 30x106 psi, and a yield stress of 3x104 psi. The beam must be at least 0.5 inches wide. The width (w) must be less than twice the depth (d).

Optimize the beam column design to minimize the weight. The compressive stress due to Py is
$$\sigma_y = \frac{P_y}{b\;d}$$
The compressive stress due to Px is
$$\sigma_x = \frac{P_x \ell d}{2 I_{zz}} = \frac{6 P_x \ell}{b \; d^2}$$
where the length l of the beam is 50 in and `I_{zz}` is the moment of inertia. The load where axial buckling starts is
$$P_{y,crit}=\frac{\pi^2 E I_{zz}}{4 \ell^2} = \frac{\pi^2 E b d^3}{48\ell^2}$$
Determine the optimal solution and show the solution graphically on a contour plot that shows the constraints and weight objective function versus the design variables (beam width and beam depth).
Solution
from numpy import pi
m = GEKKO(remote=False)
# Constants
Px = 10 # Transverse load (lb)
Py = 25 # Axial load (lb)
Ln = 50 # Beam length (in)
rho = 0.3 # Material density (lb/in^3)
S_y = 30000 # Yield stress (psi)
E = 30e6 # Young's modulus
# Variables
b = m.Var(lb=0.5) # Beam width (in)
d = m.Var(lb=1e-3) # Beam depth (in)
weight = m.Var(lb=1e-3) # Beam weight (lb)
# Intermediate calculations
I_zz = b*d**3/12 # Moment of Inertia
x_stress = m.Var(ub=S_y) # Compressive stress due to Px
y_stress = m.Var(ub=S_y) # Compressive stress due to Py
# Intermediate: Axial Buckling Load
Py_ab = m.Intermediate(pi**2*E*I_zz/(4*Ln**2))
# Equations
m.Equations([
weight == b*d*Ln*rho,
y_stress*(b*d)==Py,
x_stress*(2*I_zz)==Px*Ln*d,
Py_ab >= Py,
b <= 2*d
])
# Objective
m.Minimize(weight)
# Solve
m.options.SOLVER = 3
m.solve()
print('Weight: ' + str(weight[0]))
print('Depth: ' + str(d[0]))
print('Width: ' + str(b[0]))
print('Vertical stress: ' + str(x_stress[0]))
print('Horizontal stress: ' + str(y_stress[0]))
print('Axial Buckling Load: ' + str(Py_ab[0]))
The optimal solution is:
Optimal Weight: 3.354101916 Optimal Depth: 0.44721359774 Optimal Width: 0.5 Optimal Vertical stress: 30000.0 Optimal Horizontal stress: 111.80340055 Optimal Axial Buckling Load: 110.34553341
Show solution graphically similar to the Two Bar Truss design optimization.