Minimax and Maximin Optimization
A minimax problem seeks to minimize the maximum value of a number of decision variables. It is sometimes applied to minimize the possible loss for a worst case (maximum loss) scenario. A maximin problem maximizes the minimum value. It is used to maximize the minimum objective (such as profit or revenue) for all potential scenarios.
Minimax
Suppose that we want to minimize the maximum of 3 variables and the sum of those variables must add up to 15. This problem is posed as:
min max(x1,x2,x3) s.t. x1 + x2 + x3 = 15
The minimax problem is transformed for efficient solution by gradient-based optimization solvers that require continuous first and second derivatives. Posing the problem in this way allows rapid convergence to a solution. The minimax problem can be alternatively expressed by minimizing an additional variable Z that is an upper bound for each of the individual variables (x1, x2, and x3).
min Z
s.t. x1 + x2 + x3 = 15
Z >= x1
Z >= x2
Z >= x3
The minimax optimization solution is now a minimization with additional inequality constraints with Z. Python Gekko solves the minimax problem.
m = GEKKO(remote=False)
x1,x2,x3,Z = m.Array(m.Var,4)
m.Minimize(Z)
m.Equation(x1+x2+x3==15)
m.Equations([Z>=x1,Z>=x2,Z>=x3])
m.solve()
print('x1: ',x1.value[0])
print('x2: ',x2.value[0])
print('x3: ',x3.value[0])
print('Z: ',Z.value[0])
The solution is that all of the variables are equal to 5 to minimize the maximum value. The sum of the variables must equal 15 so this is optimal solution.
x1: 5.0 x2: 5.0 x3: 5.0 Z: 4.9999999901
The value of Z is not exactly equal to 5. This is because of small numerical errors from the IPOPT optimizer. The optimizer reports a successful solution when a precision tolerance is met.
Maximin
Suppose that we instead want to maximize the minimum of 3 variables and the sum of those variables must add up to 15. This problem is posed as:
max min(x1,x2,x3) s.t. x1 + x2 + x3 = 15
The maximin problem is likewise transformed with an additional variable Z. However, Z is now a lower bound for each of the individual variables (x1, x2, and x3).
max Z
s.t. x1 + x2 + x3 = 15
Z <= x1
Z <= x2
Z <= x3
The maximin optimization solution is now a maximization problem with additional inequality constraints with Z. Python Gekko also solves the maximin problem.
m = GEKKO(remote=False)
m.options.SOLVER = 1
x1,x2,x3,Z = m.Array(m.Var,4)
m.Maximize(Z)
m.Equation(x1+x2+x3==15)
m.Equations([Z<=x1,Z<=x2,Z<=x3])
m.solve()
print('x1: ',x1.value[0])
print('x2: ',x2.value[0])
print('x3: ',x3.value[0])
print('Z: ',Z.value[0])
The solution is that all of the variables are equal to 5 to maximize the minimum value. The sum of the variables must equal 15 so this is same optimal solution as the minimax problem.
x1: 5.0 x2: 5.0 x3: 5.0 Z: 5.0
The value of Z is now exactly equal to 5. This is because of the switch to the APOPT optimizer (m.options.SOLVER=1) that is an active-set SQP optimizer as opposed to the interior point IPOPT optimizer that uses a barrier function.
Solve Minimax Problem Online
The solution to Minimax problem can be determined by expressing the optimization problem in the APMonitor Modeling Language and solved through a web browser. To solve this simple example problem, select the link below:
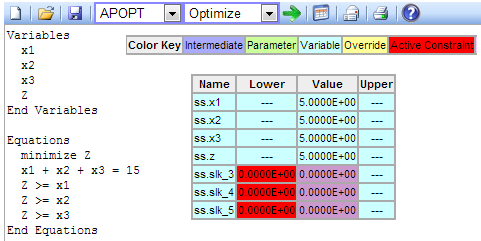
Example #1: Click to Solve minimax Optimization Problem
The solution is shown above with all variables being equal to a value of 5. This solution is the minimum possible solution out of the maximum of all variable (x1, x2, x3) combinations. The additional slack variables are automatically added to the model to transform the inequality constraints (e.g. Z >= x1) into equality constraints (e.g. Z = x1 + slk, slk >= 0).
Integer Solution to Minimax Problem
Suppose that the variables in the above example problem are required to be integer (1, 2, 3, etc) values instead of continuous values. In this case, the solution would be the same because the continuous problem has an integer solution. However, if the sum of the variables (x1 + x2 + x3) were set equal to 16 instead of 15, the solution would be different.
In Python Gekko an integer solution can be obtained with integer=True and by switching to the APOPT solver with m.options.solver=1.
m = GEKKO(remote=False)
x1,x2,x3,Z = m.Array(m.Var,4,integer=True)
m.Minimize(Z)
m.Equation(x1+x2+x3==16)
m.Equations([Z>=x1,Z>=x2,Z>=x3])
m.options.solver=1
m.solve()
print('x1: ',x1.value[0])
print('x2: ',x2.value[0])
print('x3: ',x3.value[0])
print('Z: ',Z.value[0])
Valid solutions are any combination of 15,15,16. To require that the variables have an integer value in APMonitor, the prefix int is added.
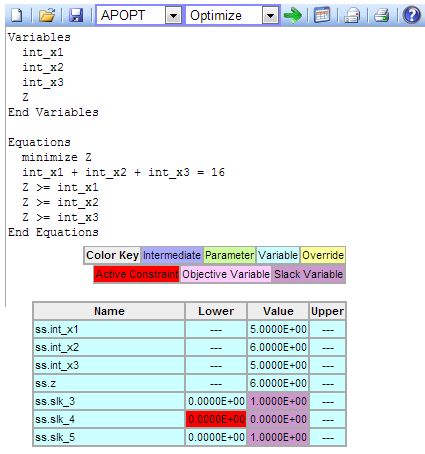
Example #2: Click to Solve minimax Problem with Integer Variables
Solving the problem with the modified variable names gives a numerical solution of x1 = 5, x2 = 6, x3 = 5. There are three potential solutions with one of the variables being equal to 6 while the others are equal to 5.
Mixed Integer Nonlinear Programming (MINLP)
Selecting a solver that does not handle integer variables (such as IPOPT) results in a relaxed continuous variable solution because the integer variable requirements are ignored. Selecting a mixed integer nonlinear programming (MINLP) solver such as APOPT will attempt to find an integer solution.
Maximin Optimization Problem
The maximin problem is similar to the minimax problem but it seeks to maximize the minimum of all available options.
max min (x1,x2,x3) s.t. x1 + x2 + x3 = 17
The minimax problem can be alternatively posed by maximizing an additional variable Z that is a lower bound for each of the individual variables.
max Z
s.t. x1 + x2 + x3 = 17
Z <= x1
Z <= x2
Z <= x3
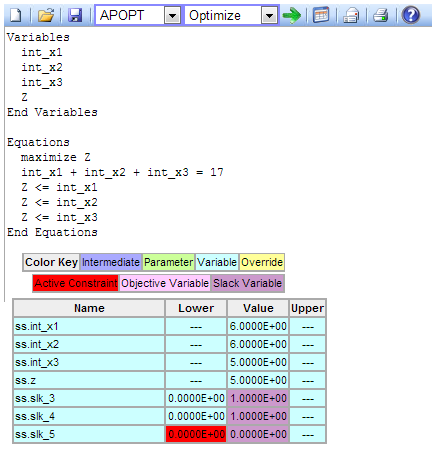
Example #3: Click to Solve maximin Problem with Integer Variables
Solving the maximin problem with integer variables gives a numerical solution of x1 = 6, x2 = 6, x3 = 5. There are three potential solutions with one of the variables being equal to 5 while the others are equal to 6.