TCLab Impulse Response
 |  |  |  |  |
|---|
Objective: Compare an analytic solution of a FOPDT model with an impulse response of the TCLab.
Perform a two minute impulse test with heater 1 to 70% starting at 10 seconds for 1 minute (between 10 and 70 seconds) and continue until 120 seconds.
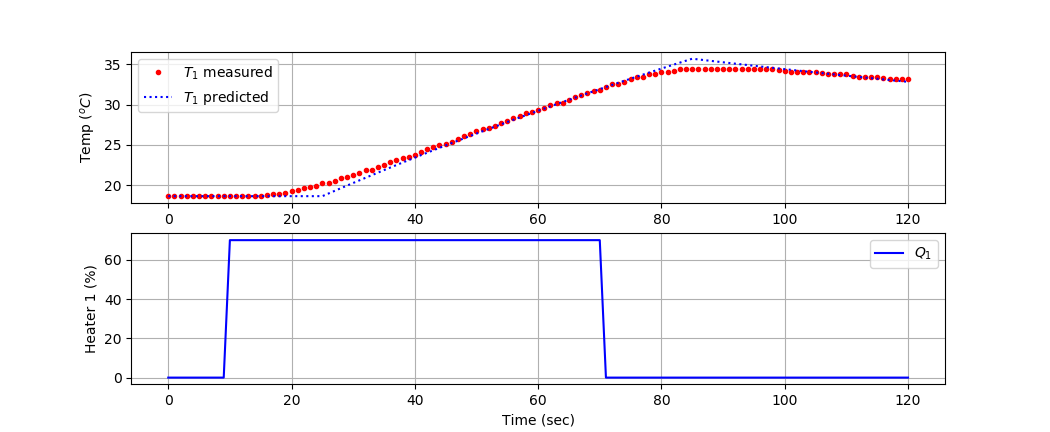
Create a plot of the temperature response over 2 minutes that shows the heater level (%), measured temperature (oC), and predicted temperature (oC). Instead of using an ODE solver, derive an analytical solution and simulate a first order plus dead time (FOPDT) model. The FOPDT model is:
$$\tau_p \frac{dT'}{dt} = -T' + K_p \, Q'\left(t-\theta_p\right)$$
where `T'=T-T_{ss}` and `Q'=Q-Q_{ss}` are deviation variables with steady-state initial conditions `T_{ss}=T_{ambient}` and `Q_{ss}=0 \%`. Use the following script to generate a plot (Impulse_Response.png) and data file (Impulse_Response.csv).
import matplotlib.pyplot as plt
import pandas as pd
import tclab
import time
try:
# read Step_Response.csv if it exists
data = pd.read_csv('Impulse_Response.csv')
tm = data['Time'].values
Q1 = data['Q1'].values
T1 = data['T1'].values
except:
# generate data only once
n = 120 # Number of second time points (2 min)
tm = np.linspace(0,n,n+1) # Time values
lab = tclab.TCLab()
T1 = [lab.T1]
Q1 = np.zeros(n+1)
Q1[10:71] = 70.0
for i in range(n):
lab.Q1(Q1[i])
time.sleep(1)
print(lab.T1)
T1.append(lab.T1)
lab.close()
# Save data file
data = np.vstack((tm,Q1,T1)).T
np.savetxt('Impulse_Response.csv',data,delimiter=',',\
header='Time,Q1,T1',comments='')
# Create Figure
plt.figure(figsize=(10,7))
ax = plt.subplot(2,1,1)
ax.grid()
plt.plot(tm,T1,'r.',label=r'$T_1$')
plt.ylabel(r'Temp ($^oC$)')
ax = plt.subplot(2,1,2)
ax.grid()
plt.plot(tm,Q1,'b-',label=r'$Q_1$')
plt.ylabel(r'Heater 1 (%)')
plt.xlabel('Time (sec)')
plt.legend()
plt.savefig('Impulse_Response.png')
plt.show()
Use values of `K_p`=0.9oC/%, `\tau_p`=190 sec, and `\theta_p`=15 sec to compute the analytic solution.
Solution
Apply the Laplace transform to each of the terms in the FOPDT equation. Because the Laplace transform is a linear operator, each term can be transformed separately. Because T'(t) is a deviation variable, the initial condition at the initial time is T'(0)=0.
$$\mathcal{L}\left(\tau_p \frac{dT'(t)}{dt}\right) = \tau_p \left(s \, T(s) - T'(0)\right) = \tau_p s \, T(s)$$
$$\mathcal{L}\left(-T'(t)\right) = -T(s)$$
$$\mathcal{L}\left(K_p \, Q'(t-\theta_p)\right) = K \, Q(s) \, e^{-\theta_p s}$$
Putting these terms together gives the first-order differential equation in the Laplace domain.
$$\tau_p \, s \, T(s) = -T(s) + K_p \, Q(s) \, e^{-\theta_p s}$$
The T(s) terms are collected to the left side of the equation.
$$T(s) = \frac{K_p}{\tau_p s + 1} e^{-\theta_p s} Q(s)$$
The differential equation as a function of time (t) is now an algebraic equation in the Laplace domain (s). The input function is:
$$Q(s) = \frac{70}{s} \, e^{-10 s} - \frac{70}{s} \, e^{-70 s}$$
This gives an expression for T(s) in Laplace form.
$$T(s) = \frac{K_p}{\tau_p s + 1} e^{-\theta_p s} \left(\frac{70}{s} \, e^{-10 s} - \frac{70}{s} \, e^{-70 s}\right)$$
With `\theta_p`=15 sec, an inverse Laplace transform gives the analytic solution for T(t).
$$T(t) = 70 \, K_p \, \left(1-e^{-\frac{t-25}{\tau_p}}\right) S(t-25) - 70 \, K_p \, \left(1-e^{-\frac{t-85}{\tau_p}}\right) S(t-85)$$
import matplotlib.pyplot as plt
import pandas as pd
import tclab
import time
try:
# read Step_Response.csv if it exists
data = pd.read_csv('Impulse_Response.csv')
tm = data['Time'].values
Q1 = data['Q1'].values
T1 = data['T1'].values
except:
# generate data only once
n = 120 # Number of second time points (2 min)
tm = np.linspace(0,n,n+1) # Time values
lab = tclab.TCLab()
T1 = [lab.T1]
Q1 = np.zeros(n+1)
Q1[10:71] = 70.0
for i in range(n):
lab.Q1(Q1[i])
time.sleep(1)
print(lab.T1)
T1.append(lab.T1)
lab.close()
# Save data file
data = np.vstack((tm,Q1,T1)).T
np.savetxt('Impulse_Response.csv',data,delimiter=',',\
header='Time,Q1,T1',comments='')
# Analytic solution
nt = len(tm)
Kp = 0.9
taup = 190.0
s1 = np.zeros(nt)
s1[25:] = 1.0
s2 = np.zeros(nt)
s2[85:] = 1.0
T1s = 70 * Kp * (1.0-np.exp(-(tm-25.0)/taup))*s1 - \
70 * Kp * (1.0-np.exp(-(tm-85.0)/taup))*s2 + T1[0]
# Create Figure
plt.figure(figsize=(10,7))
ax = plt.subplot(2,1,1)
ax.grid()
plt.plot(tm,T1,'r.',label=r'$T_1$ measured')
plt.plot(tm,T1s,'b:',label=r'$T_1$ predicted')
plt.ylabel(r'Temp ($^oC$)')
plt.legend()
ax = plt.subplot(2,1,2)
ax.grid()
plt.plot(tm,Q1,'b-',label=r'$Q_1$')
plt.ylabel(r'Heater 1 (%)')
plt.xlabel('Time (sec)')
plt.legend()
plt.savefig('Impulse_Response.png')
plt.show()
