The flow rate of cooling fluid through a system is regulated by a valve. The pressure generated by the pump is constant.

$$\Delta P_{pump}=100 \,\mathrm{bar}$$

The cooling fluid has a specific gravity of 1.1. As a first step, characterize the valve without the system pressure drop. In a second step, determine the best valve trim for a linear relationship between lift and flow for the installed valve.

Part I: Valve Characterization

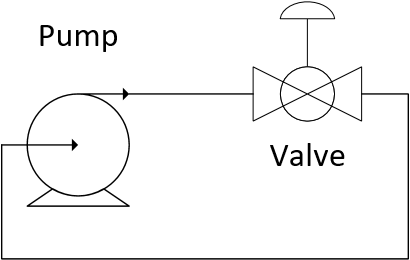
Plot the relationship between flow `q` and valve lift `l` for the valve characterized by the design equation.

$$q = C_v f(l) \sqrt{\frac{\Delta P_v}{g_s}}$$

with `C_v = 2` and either a linear lift function `f(l)=l` or an equal percentage lift function `f(l)=R^{l-1}` with `R=20`.

Solution, Part I

import numpy as np
import matplotlib.pyplot as plt

## Lift functions for two different valve trim types
def f_lin(x):
    return x             # linear valve trim
def f_ep(x):
    R = 20
    return R**(x-1)      # equal percentage valve trim (R = 20-50)

lift = np.linspace(0,1)  # equally spaced points between 0 and 1

plt.figure(1)            # create new figure
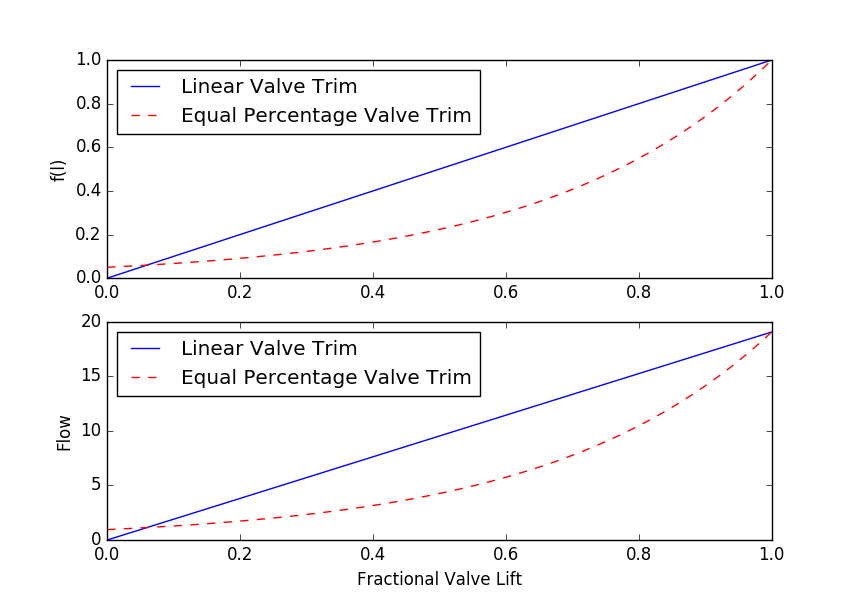
plt.title('Valve Performance - Not Installed')
plt.subplot(2,1,1)                # 2,1 subplot with 1st window
plt.plot(lift,f_lin(lift),'b-')   # linear valve
plt.plot(lift,f_ep(lift),'r--')   # equal percentage
plt.ylabel('f(l)')
plt.legend(['Linear Valve Trim','Equal Percentage Valve Trim'])

g_s = 1.1                # specific gravity of fluid
def q(x,f,Cv,DPv):
    return Cv * f(x) * np.sqrt(DPv/g_s)   # flow through a valve

## Intrinsic valve performance
# no process equipment - all pressure drop is across valve
DPt = 100 # Total pressure generated by pump (constant)
Cv = 2    # Valve Cv
flow_lin = q(lift,f_lin,Cv,DPt)  # flow with linear valve
flow_ep  = q(lift,f_ep,Cv,DPt)   # flow with equal percentage

plt.subplot(2,1,2)               # 2,1 subplot with 2nd window
plt.plot(lift,flow_lin,'b-')     # plot linear valve response
plt.plot(lift,flow_ep,'r--')     # plot equal percentage valve
plt.ylabel('Flow')
plt.legend(['Linear Valve Trim','Equal Percentage Valve Trim'])
plt.xlabel('Fractional Valve Lift')
plt.show()

[$[Get Code]]

Part II: Installed Valve

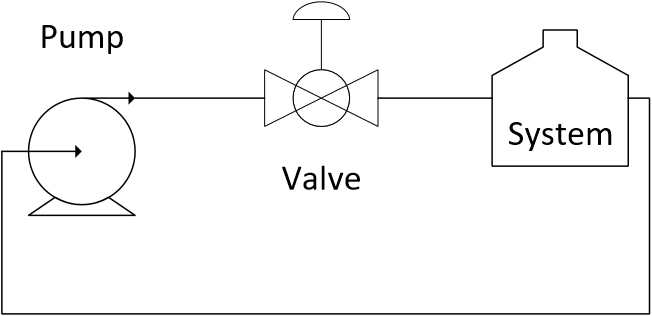
The pressure drop across the system (without the valve) follows the following correlation between pressure drop `\Delta P_{system}` and flow rate `q`.

$$\Delta P_{system} = 2 q^2$$

Plot the relationship between flow `q` and valve lift `l` for the system and valve with `C_v = 2` and either a linear lift function `f(l)=l` or an equal percentage lift function `f(l)=R^{l-1}` with `R=20`.

Interactive Valve Design Widget GitHub Colab

🚰 APMonitor Valve Design App

Solution, Part II

The first step in this solution is to relate the pressure drop across the valve and the system to the pressure generated by the pump.

$$\Delta P_{pump} = \Delta P_v + \Delta P_{system}$$

with

$$\Delta P_{pump} = 100$$

$$\Delta P_v = g_s \left(\frac{q}{C_v f(l)}\right)^2$$

$$\Delta P_{system} = 2 q^2$$

This gives a combined equation in terms of lift `l` and flow `q`.

$$100 = g_s \left(\frac{q}{C_v f(l)}\right)^2 + 2 q^2$$

Algebraic manipulation is then used to obtain flow as a function of lift `q(l)` for the valve and system.

$$q(l) = \sqrt{\frac{100\left(C_v f(l)\right)^2}{(g_s + 2 \left(C_v f(l)\right)^2)}}$$

import numpy as np
import matplotlib.pyplot as plt

DPt = 100    # Total pressure generated by pump (constant)
Cv = 2       # Valve Cv
g_s = 1.1    # specific gravity of fluid
lift = np.linspace(0,1)  # equally spaced points between 0 and 1

## Lift functions for two different valve trim types
def f_lin(x):
    return x             # linear valve trim
def f_ep(x):
    R = 20
    return R**(x-1)      # equal percentage valve trim (R = 20-50)

## Installed valve performance
# pressure drop across the system (without valve)
c1 = 2
def DPe(q):
    return c1 * q**2

# valve and process equipment flow with 100 bar pressure drop
def qi(x,f,Cv):
    return np.sqrt((Cv*f(x))**2*DPt / (g_s + (Cv*f(x))**2 * c1))

# Process equipment + Valve performance
flow_lin = qi(lift,f_lin,Cv)  # flow through linear valve
flow_ep  = qi(lift,f_ep,Cv)   # flow through equal percentage valve

plt.figure(2)
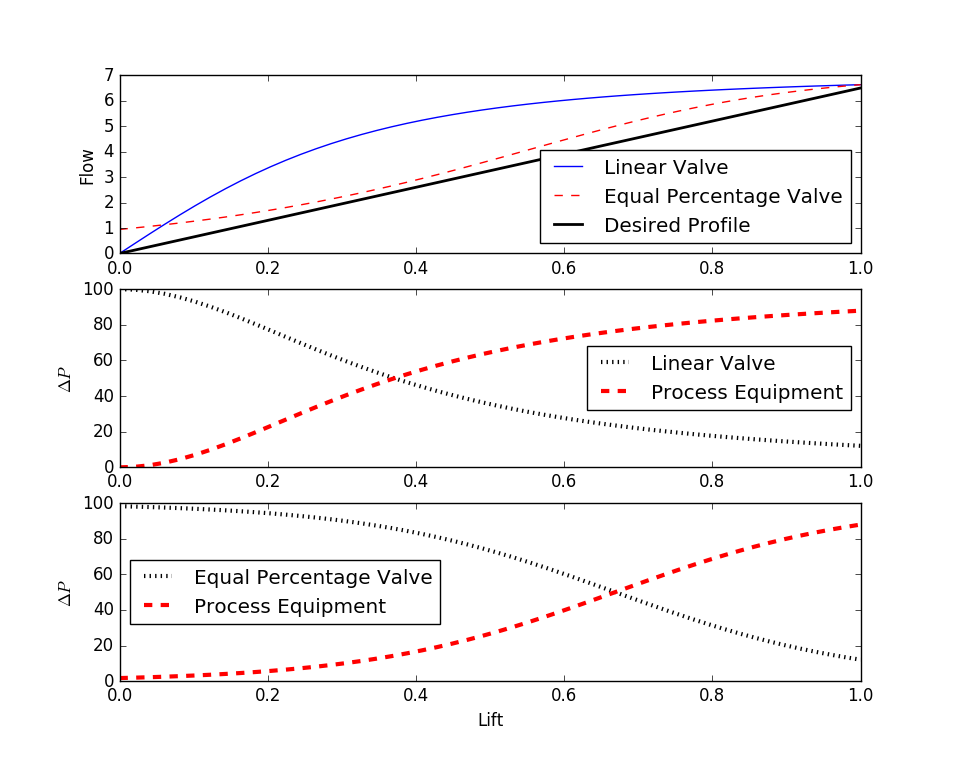
plt.title('Valve Performance - Installed')
plt.subplot(3,1,1)
plt.plot(lift,flow_lin,'b-',label='Linear Valve')
plt.plot(lift,flow_ep,'r--',label='Equal Percentage Valve')
plt.plot([0,1],[0,6.5],'k-',linewidth=2,label='Desired Profile')
plt.legend(loc='best')
plt.ylabel('Flow')

plt.subplot(3,1,2)
plt.plot(lift,DPt-DPe(flow_lin),'k:',linewidth=3)
plt.plot(lift,DPe(flow_lin),'r--',linewidth=3)
plt.legend(['Linear Valve','Process Equipment'],loc='best')
plt.ylabel(r'$\Delta P$')

plt.subplot(3,1,3)
plt.plot(lift,DPt-DPe(flow_ep),'k:',linewidth=3)
plt.plot(lift,DPe(flow_ep),'r--',linewidth=3)
plt.legend(['Equal Percentage Valve','Process Equipment'],loc='best')
plt.ylabel(r'$\Delta P$')
plt.xlabel('Lift')

plt.show()

[$[Get Code]]

What to Turn In

This assignment consists of two parts.

• Part I: Valve Characterization: Generate a plot of the relationship between flow (`q`) and valve lift (`l`) for the valve without the system pressure drop. Generate two plots: one using a linear lift function (`f(l) = l`) and one using an equal percentage lift function (`f(l) = R^{l-1}`, with `R = 20`).
• Part II: Installed Valve: Generate a plot of the relationship between flow (`q`) and valve lift (`l`) for the valve installed in the system (including the system pressure drop). Generate two plots: one using a linear lift function (`f(l) = l`) and one using an equal percentage lift function (`f(l) = R^{l-1}`, with `R = 20`).

Important Parameters:

• Pump pressure (`\Delta P_{pump} = 100` bar)
• Specific gravity = 1.1
• `C_v = 2`
• System pressure drop: `\Delta P_{system} = 2q^2`

Generative AI Learning

Use these prompts to test your understanding after completing the exercise. Direct the AI - do not let it do the sizing for you.

App: Explore sizing and characteristics in the Valve Design app - compare linear and equal-percentage trim, and watch the inherent characteristic morph into the installed characteristic as the system pressure drop share changes; find the trim that stays most linear installed.

What to Turn In

Submit a short report (PDF, 1-2 pages) that curates your results into a demonstration of what you learned. You may use Generative AI to help write the report, but you must guide it to the correct calculations, justifications, and assumptions. Answer these questions:

1. Show your Cv calculation for the assigned service, the selected valve/trim, and the sizing margin with justification.
2. Include the app's installed-characteristic plots for linear vs equal-percentage trim at your pressure-drop ratio. Which is more linear installed, and why?
3. State your fail-safe choice (fail-open or fail-closed) for this service and defend it with the safety consequence analysis.
4. From the audit prompt: one what-if that changed (or confirmed) your selection.