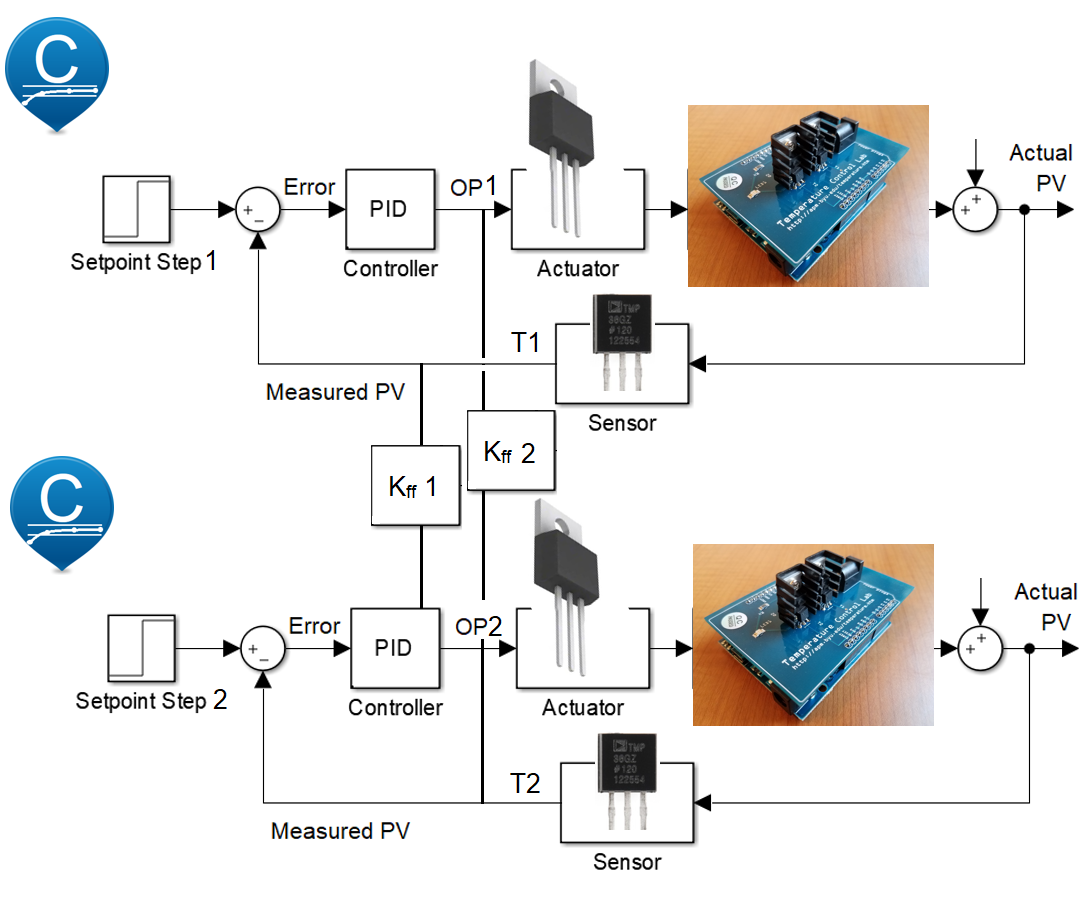
Interacting PID Control
Design an interacting PID controllers for the two heaters and sensors on the TCLab. Obtain PID tuning constants `K_c`, `\tau_I`, `\tau_D`, and `K_{ff}` from IMC correlations. Use the tuning constants for PID control of temperature for both `T_1` and `T_2`.
Demonstrate step changes in temperature set point and comment on the performance of the Arduino controller using the calculated constants. Tune the controller by adjusting the constants to improve performance. Comment on the difference between IMC tuning constants and the improved tuning constants in terms of rise time, overshoot, decay ratio, heater fluctuations, or other relevant performance criteria. Report the integral absolute error (IAE) over 10 minutes with setpoint changes given in the test script.
$$IAE_{control} = \sum_{i=0}^n \left| T_{1,SP,i} - T_{1,meas,i} \right| + \left| T_{2,SP,i} - T_{2,meas,i} \right|$$
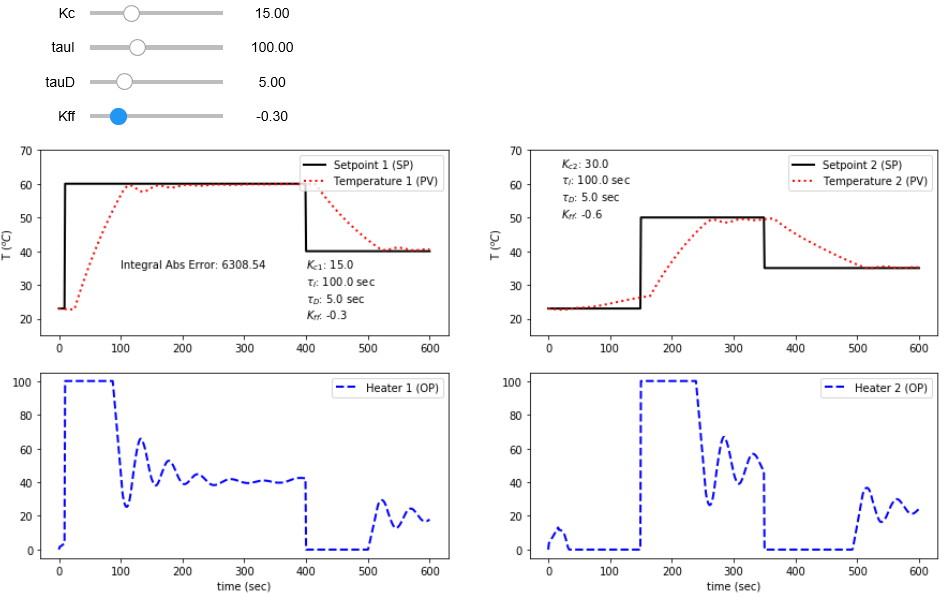
Simulate a PID Controller with one of the models determined from parameter estimation such as with the IPython script.
%matplotlib inline
import matplotlib.pyplot as plt
from scipy.integrate import odeint
import ipywidgets as wg
from IPython.display import display
n = 601 # time points to plot
tf = 600.0 # final time
# TCLab FOPDT
Kp = 1.1
Kd = 0.65
taup = 190.0
thetap = 25.0
T1_0 = 21.3
T2_0 = 21.3
y0 = [T1_0,T2_0]
Kff = -Kd/Kp
def process(y,t,u1,u2):
y1,y2 = y
dy1dt = (1.0/taup) * (-(y1-y0[0]) + Kp * u1 + Kd * (y2-y1))
dy2dt = (1.0/taup) * (-(y2-y0[1]) + (Kp/2.0) * u2 + Kd * (y1-y2))
return [dy1dt,dy2dt]
def pidPlot(Kc,tauI,tauD,Kff):
y0 = [23.0,23.0]
t = np.linspace(0,tf,n) # create time vector
P1 = np.zeros(n) # initialize proportional term
I1 = np.zeros(n) # initialize integral term
D1 = np.zeros(n) # initialize derivative term
FF1 = np.zeros(n) # initialize feedforward term
e1 = np.zeros(n) # initialize error
P2 = np.zeros(n) # initialize proportional term
I2 = np.zeros(n) # initialize integral term
D2 = np.zeros(n) # initialize derivative term
FF2 = np.zeros(n) # initialize feedforward term
e2 = np.zeros(n) # initialize error
OP1 = np.zeros(n) # initialize controller output
OP2 = np.zeros(n) # initialize disturbance
PV1 = np.ones(n)*y0[0] # initialize process variable
PV2 = np.ones(n)*y0[1] # initialize process variable
SP1 = np.ones(n)*y0[0] # initialize setpoint
SP2 = np.ones(n)*y0[1] # initialize setpoint
SP1[10:] = 60.0 # step up
SP1[400:] = 40.0 # step up
SP2[150:] = 50.0 # step down
SP2[350:] = 35.0 # step down
Kc1 = Kc
Kc2 = Kc*2.0
Kff1 = Kff
Kff2 = Kff*2.0
iae = 0.0
# loop through all time steps
for i in range(1,n):
# simulate process for one time step
ts = [t[i-1],t[i]] # time interval
heaters = (OP1[max(0,i-int(thetap))],OP2[max(0,i-int(thetap))])
y = odeint(process,y0,ts,args=heaters)
y0 = y[1] # record new initial condition
# calculate new OP with PID
PV1[i] = y[1][0] # record T1 PV
PV2[i] = y[1][1] # record T2 PV
iae += np.abs(SP1[i]-PV1[i]) + np.abs(SP2[i]-PV2[i])
dt = t[i] - t[i-1] # calculate time step
# PID for loop 1
e1[i] = SP1[i] - PV1[i] # calculate error = SP - PV
P1[i] = Kc1 * e1[i] # calculate proportional term
I1[i] = I1[i-1] + (Kc1/tauI) * e1[i] * dt # calculate integral term
D1[i] = -Kc * tauD * (PV1[i]-PV1[i-1])/dt # calculate derivative
FF1[i] = Kff1 * (PV2[i]-PV1[i])
OP1[i] = P1[i] + I1[i] + D1[i] + FF1[i] # calculate new output
if OP1[i]>=100:
OP1[i] = 100.0
I1[i] = I1[i-1] # reset integral
if OP1[i]<=0:
OP1[i] = 0.0
I1[i] = I1[i-1] # reset integral
# PID for loop 2
e2[i] = SP2[i] - PV2[i] # calculate error = SP - PV
P2[i] = Kc2 * e2[i] # calculate proportional term
I2[i] = I2[i-1] + (Kc2/tauI) * e2[i] * dt # calculate integral term
D2[i] = -Kc2 * tauD * (PV2[i]-PV2[i-1])/dt # calculate derivative
FF2[i] = Kff2 * (PV1[i]-PV2[i])
OP2[i] = P2[i] + I2[i] + D2[i] + FF2[i] # calculate new output
if OP2[i]>=100:
OP2[i] = 100.0
I2[i] = I2[i-1] # reset integral
if OP2[i]<=0:
OP2[i] = 0.0
I2[i] = I2[i-1] # reset integral
# plot PID response
plt.figure(1,figsize=(15,7))
plt.subplot(2,2,1)
plt.plot(t,SP1,'k-',linewidth=2,label='Setpoint 1 (SP)')
plt.plot(t,PV1,'r:',linewidth=2,label='Temperature 1 (PV)')
plt.ylabel(r'T $(^oC)$')
plt.text(100,35,'Integral Abs Error: ' + str(np.round(iae,2)))
plt.text(400,35,r'$K_{c1}$: ' + str(np.round(Kc,1)))
plt.text(400,30,r'$\tau_I$: ' + str(np.round(tauI,0)) + ' sec')
plt.text(400,25,r'$\tau_D$: ' + str(np.round(tauD,0)) + ' sec')
plt.text(400,20,r'$K_{ff}$: ' + str(np.round(Kff1,2)))
plt.ylim([15,70])
plt.legend(loc=1)
plt.subplot(2,2,2)
plt.plot(t,SP2,'k-',linewidth=2,label='Setpoint 2 (SP)')
plt.plot(t,PV2,'r:',linewidth=2,label='Temperature 2 (PV)')
plt.ylabel(r'T $(^oC)$')
plt.text(20,65,r'$K_{c2}$: ' + str(np.round(Kc*2,1)))
plt.text(20,60,r'$\tau_I$: ' + str(np.round(tauI,0)) + ' sec')
plt.text(20,55,r'$\tau_D$: ' + str(np.round(tauD,0)) + ' sec')
plt.text(20,50,r'$K_{ff}$: ' + str(np.round(Kff2,2)))
plt.ylim([15,70])
plt.legend(loc=1)
plt.subplot(2,2,3)
plt.plot(t,OP1,'b--',linewidth=2,label='Heater 1 (OP)')
plt.legend(loc='best')
plt.xlabel('time (sec)')
plt.subplot(2,2,4)
plt.plot(t,OP2,'b--',linewidth=2,label='Heater 2 (OP)')
plt.legend(loc='best')
plt.xlabel('time (sec)')
print('PID with Feedforward Simulator: Adjust Kc, tauI, tauD, and Kff ' + \
'to achieve lowest Integral Abs Error')
# ITAE Setpoint Tracking PI Tuning
Kc = (0.586/Kp)*(thetap/taup)**(-0.916); tauI = taup/(1.03-0.165*(thetap/taup))
print(f'ITAE Recommended: Kc={Kc:4.2f}, tauI={tauI:5.1f}, tauD=0, Kff={Kff:4.2f}')
# IMC Aggressive PID Tuning
tauc = max(0.1*taup,0.8*thetap); Kc = (1/Kp)*(taup+0.5*taup)/(tauc+0.5*thetap)
tauI = taup+0.5*thetap; tauD = taup*thetap/(2*taup+thetap); Kff=-Kd/Kp
print(f'IMC Recommended: Kc={Kc:4.2f}, tauI={tauI:5.1f}, tauD={tauD:4.2f}, Kff={Kff:4.2f}')
Kc_slide = wg.FloatSlider(value=Kc,min=0.0,max=50.0,step=1.0)
tauI_slide = wg.FloatSlider(value=tauI,min=20.0,max=250.0,step=1.0)
tauD_slide = wg.FloatSlider(value=tauD,min=0.0,max=20.0,step=1.0)
Kff_slide = wg.FloatSlider(value=Kff,min=-0.5,max=0.5,step=0.1)
wg.interact(pidPlot, Kc=Kc_slide, tauI=tauI_slide, tauD=tauD_slide,Kff=Kff_slide)
print('')
Below is basic code in Python that demonstrates how to implement a PID controller. On each cycle of the controller, the temperatures are measured (a.T1 and a.T2), the PID controller produces new outputs (OP1=pid(a.T1) and OP2=pid(a.T2)), and the PID recommended value for the heater is implemented (a.Q1(OP1) and a.Q2(OP2)). The loop pauses for the 1.0 second to wait until the next sample time.
import time
import numpy as np
from simple_pid import PID
# Connect to Arduino
a = tclab.TCLab()
# Create PID controllers
pid1 = PID(Kp=2,Ki=2/136,Kd=0,\
setpoint=40,sample_time=1.0,output_limits=(0,100))
pid2 = PID(Kp=4,Ki=4/136,Kd=0,\
setpoint=35,sample_time=1.0,output_limits=(0,100))
for i in range(600): # 10 minutes (600 sec)
# pid control
OP1 = pid1(a.T1)
OP2 = pid2(a.T2)
a.Q1(OP1)
a.Q2(OP2)
# print line
print('Heater: ' + str(round(OP1,2)) + '%' + \
' T1 PV: ' + str(a.T1) + 'degC' + \
' T1 SP: ' + str(pid1.setpoint) + 'degC')
# wait for next sample time
time.sleep(pid.sample_time)
It is suggested to tune the controller in simulation before implementing with an Arduino. Tuning on a device that takes 10 minutes per test is much slower than running a PID controller in simulation. Once optimized PID tuning values are obtained, demonstrate the performance with the physical control lab.
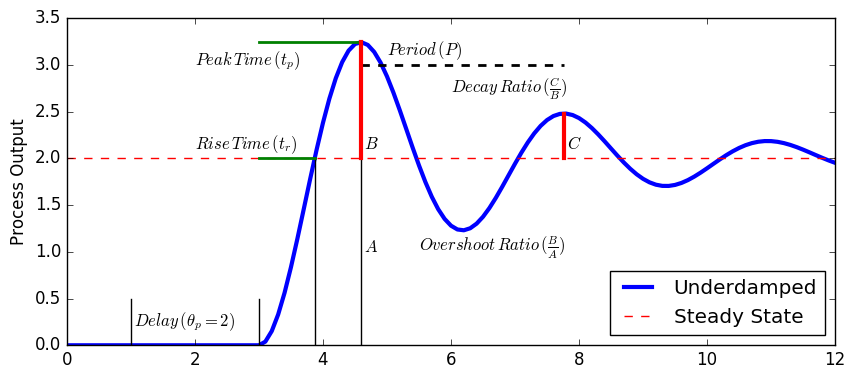
Tune the PID controller to minimize the integral absolute error (IAE). Quantify the controller performance in terms of settling time, decay ratio, overshoot ratio, peak time, and rise time. Use the following code to test the PID controller.
Switch animate=False to not create plots in Jupyter notebook. Insert the four PID parameters. The PID controller for temperature 2 uses double the controller gain and feedforward gain.
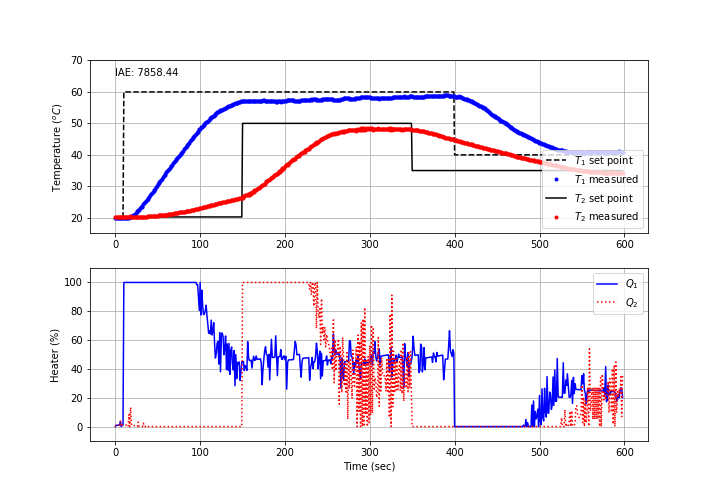
import numpy as np
import time
import matplotlib.pyplot as plt
from scipy.integrate import odeint
#-----------------------------------------
# PID controller performance for the TCLab
#-----------------------------------------
# PID Parameters
Kc = 5.0
tauI = 120.0 # sec
tauD = 2.0 # sec
Kff = -0.3
# Animate Plot?
animate = True
if animate:
try:
from IPython import get_ipython
from IPython.display import display,clear_output
get_ipython().run_line_magic('matplotlib', 'inline')
ipython = True
print('IPython Notebook')
except:
ipython = False
print('Not IPython Notebook')
#-----------------------------------------
# PID Controller with Feedforward
#-----------------------------------------
# inputs ---------------------------------
# sp = setpoint
# pv = current temperature
# pv_last = prior temperature
# ierr = integral error
# dt = time increment between measurements
# outputs --------------------------------
# op = output of the PID controller
# P = proportional contribution
# I = integral contribution
# D = derivative contribution
def pid(sp,pv,pv_last,ierr,dt,d,cid):
# Parameters in terms of PID coefficients
if cid==1:
# controller 1
KP = Kc
Kf = Kff
else:
# controller 2
KP = Kc * 2.0
Kf = Kff * 2.0
KI = Kc/tauI
KD = Kc*tauD
# ubias for controller (initial heater)
op0 = 0
# upper and lower bounds on heater level
ophi = 100
oplo = 0
# calculate the error
error = sp-pv
# calculate the integral error
ierr = ierr + KI * error * dt
# calculate the measurement derivative
dpv = (pv - pv_last) / dt
# calculate the PID output
P = KP * error
I = ierr
D = -KD * dpv
FF = Kff * d
op = op0 + P + I + D + FF
# implement anti-reset windup
if op < oplo or op > ophi:
I = I - KI * error * dt
# clip output
op = max(oplo,min(ophi,op))
# return the controller output and PID terms
return [op,P,I,D,FF]
# save txt file with data and set point
# t = time
# u1,u2 = heaters
# y1,y2 = tempeatures
# sp1,sp2 = setpoints
def save_txt(t, u1, u2, y1, y2, sp1, sp2):
data = np.vstack((t, u1, u2, y1, y2, sp1, sp2)) # vertical stack
data = data.T # transpose data
top = ('Time,Q1,Q2,T1,T2,TSP1,TSP2')
np.savetxt('validate.txt', data, delimiter=',',\
header=top, comments='')
# Connect to Arduino
a = tclab.TCLab()
# Wait until temperature is below 25 degC
print('Check that temperatures are < 25 degC before starting')
i = 0
while a.T1>=25.0 or a.T2>=25.0:
print(f'Time: {i} T1: {a.T1} T2: {a.T2}')
i += 10
time.sleep(10)
# Turn LED on
print('LED On')
a.LED(100)
# Run time in minutes
run_time = 10.0
# Number of cycles
loops = int(60.0*run_time)
tm = np.zeros(loops)
# Heater set point steps
Tsp1 = np.ones(loops) * a.T1
Tsp2 = np.ones(loops) * a.T2 # set point (degC)
Tsp1[10:] = 60.0 # step up
Tsp1[400:] = 40.0 # step down
Tsp2[150:] = 50.0 # step up
Tsp2[350:] = 35.0 # step down
T1 = np.ones(loops) * a.T1 # measured T (degC)
T2 = np.ones(loops) * a.T2 # measured T (degC)
# impulse tests (0 - 100%)
Q1 = np.ones(loops) * 0.0
Q2 = np.ones(loops) * 0.0
if not animate:
print('Running Main Loop. Ctrl-C to end.')
print(' Time SP1 PV1 Q1 SP2 PV2 Q2 IAE')
print(('{:6.1f} {:6.2f} {:6.2f} ' + \
'{:6.2f} {:6.2f} {:6.2f} {:6.2f} {:6.2f}').format( \
tm[0],Tsp1[0],T1[0],Q1[0],Tsp2[0],T2[0],Q2[0],0.0))
# Main Loop
start_time = time.time()
prev_time = start_time
dt_error = 0.0
# Integral error
ierr1 = 0.0
ierr2 = 0.0
# Integral absolute error
iae = 0.0
if not ipython:
plt.figure(figsize=(10,7))
plt.ion()
plt.show()
try:
for i in range(1,loops):
# Sleep time
sleep_max = 1.0
sleep = sleep_max - (time.time() - prev_time) - dt_error
if sleep>=1e-4:
time.sleep(sleep-1e-4)
else:
print('exceeded max cycle time by ' + str(abs(sleep)) + ' sec')
time.sleep(1e-4)
# Record time and change in time
t = time.time()
dt = t - prev_time
if (sleep>=1e-4):
dt_error = dt-sleep_max+0.009
else:
dt_error = 0.0
prev_time = t
tm[i] = t - start_time
# Read temperatures in Kelvin
T1[i] = a.T1
T2[i] = a.T2
# Disturbances
d1 = T1[i] - 23.0
d2 = T2[i] - 23.0
# Integral absolute error
iae += np.abs(Tsp1[i]-T1[i]) + np.abs(Tsp2[i]-T2[i])
# Calculate PID output
[Q1[i],P,ierr1,D,FF] = pid(Tsp1[i],T1[i],T1[i-1],ierr1,dt,d2,1)
[Q2[i],P,ierr2,D,FF] = pid(Tsp2[i],T2[i],T2[i-1],ierr2,dt,d1,2)
# Write output (0-100)
a.Q1(Q1[i])
a.Q2(Q2[i])
if not animate:
# Print line of data
print(('{:6.1f} {:6.2f} {:6.2f} ' + \
'{:6.2f} {:6.2f} {:6.2f} {:6.2f} {:6.2f}').format( \
tm[i],Tsp1[i],T1[i],Q1[i],Tsp2[i],T2[i],Q2[i],iae))
else:
if ipython:
plt.figure(figsize=(10,7))
else:
plt.clf()
# Update plot
ax=plt.subplot(2,1,1)
ax.grid()
plt.plot(tm[0:i],Tsp1[0:i],'k--',label=r'$T_1$ set point')
plt.plot(tm[0:i],T1[0:i],'b.',label=r'$T_1$ measured')
plt.plot(tm[0:i],Tsp2[0:i],'k-',label=r'$T_2$ set point')
plt.plot(tm[0:i],T2[0:i],'r.',label=r'$T_2$ measured')
plt.ylabel(r'Temperature ($^oC$)')
plt.text(0,65,'IAE: ' + str(np.round(iae,2)))
plt.legend(loc=4)
plt.ylim([15,70])
ax=plt.subplot(2,1,2)
ax.grid()
plt.plot(tm[0:i],Q1[0:i],'b-',label=r'$Q_1$')
plt.plot(tm[0:i],Q2[0:i],'r:',label=r'$Q_2$')
plt.ylim([-10,110])
plt.ylabel('Heater (%)')
plt.legend(loc=1)
plt.xlabel('Time (sec)')
if ipython:
clear_output(wait=True)
display(plt.gcf())
else:
plt.draw()
plt.pause(0.05)
# Turn off heaters
a.Q1(0)
a.Q2(0)
a.close()
# Save text file
save_txt(tm,Q1,Q2,T1,T2,Tsp1,Tsp2)
# Save Plot
if not animate:
plt.figure(figsize=(10,7))
ax=plt.subplot(2,1,1)
ax.grid()
plt.plot(tm,Tsp1,'k--',label=r'$T_1$ set point')
plt.plot(tm,T1,'b.',label=r'$T_1$ measured')
plt.plot(tm,Tsp2,'k-',label=r'$T_2$ set point')
plt.plot(tm,T2,'r.',label=r'$T_2$ measured')
plt.ylabel(r'Temperature ($^oC$)')
plt.text(0,65,'IAE: ' + str(np.round(iae,2)))
plt.legend(loc=4)
ax=plt.subplot(2,1,2)
ax.grid()
plt.plot(tm,Q1,'b-',label=r'$Q_1$')
plt.plot(tm,Q2,'r:',label=r'$Q_2$')
plt.ylabel('Heater (%)')
plt.legend(loc=1)
plt.xlabel('Time (sec)')
plt.savefig('PID_Control.png')
# Allow user to end loop with Ctrl-C
except KeyboardInterrupt:
# Disconnect from Arduino
a.Q1(0)
a.Q2(0)
print('Shutting down')
a.close()
save_txt(tm[0:i],Q1[0:i],Q2[0:i],T1[0:i],T2[0:i],Tsp1[0:i],Tsp2[0:i])
plt.savefig('PID_Control.png')
# Make sure serial connection closes with an error
except:
# Disconnect from Arduino
a.Q1(0)
a.Q2(0)
print('Error: Shutting down')
a.close()
save_txt(tm[0:i],Q1[0:i],Q2[0:i],T1[0:i],T2[0:i],Tsp1[0:i],Tsp2[0:i])
plt.savefig('PID_Control.png')
raise
print('PID test complete')
print('Kc: ' + str(Kc))
print('tauI: ' + str(tauI))
print('tauD: ' + str(tauD))
print('Kff: ' + str(Kff))
Interacting PID Control IPython Notebook
Return to Temperature Control Lab Overview

