Design Optimization

Quasi-Newton methods are a class of numerical optimization algorithms that are used to find minima or maxima of functions. They are a generalization of Newton's method, which uses the Hessian matrix of second derivatives to approximate the local curvature of a function. Quasi-Newton methods use approximate versions of the Hessian matrix that are updated as the algorithm proceeds. This allows the algorithm to more quickly converge to the optimum without needing to compute the full Hessian matrix. The most commonly used quasi-Newton methods are the Broyden–Fletcher–Goldfarb–Shanno (BFGS) and the limited memory BFGS (L-BFGS).

MATLAB Source Code

 Conjugate gradient

 Conjugate gradient

 Conjugate gradient

 Conjugate gradient

gold

 Newton's method
 Steepest descent
 Conjugate gradient
 BFGS update

 Newton's method
 Steepest descent
 Conjugate gradient
 BFGS update

$$\min_{x_1,x_2} \left(x_1^2-2 x_1 x_2 + 4 x_2^2\right)$$

$$\min_{x_1,x_2} x_1^2-2 x_1 x_2 + 4 x_2^2$$

More Advanced Solvers

The above implementations are very simple with 7-30 lines of code each. More advanced methods are implemented with Nonlinear Programming (NLP) and Mixed Integer Nonlinear Programming Solvers (MINLP) solvers such as APOPT (MINLP solver), BPOPT (NLP solver), and IPOPT (NLP solver). The following Python Gekko code demonstrates the performance with these three solvers by changing m.options.SOLVER to 1=APOPT, 2=BPOPT, 3=IPOPT.

(:source lang=python:) from gekko import GEKKO m = GEKKO() x1 = m.Var(-3) x2 = m.Var(2) m.Minimize(x1**2-2*x1*x2+4*x2**2) m.options.SOLVER = 2 # 1=APOPT, 2=BPOPT, 3=IPOPT m.solve() print(x1.value[0],x2.value[0]) (:sourceend:)

The simple objective only requires an unconstrained Quadratic Programming (QP) solver with the objective function.

$$x_1^2-2 x_1 x_2 + 4 x_2^2$$

The NLP and MINLP solvers can also solve the problem. APOPT converges in 4 iterations using 1st derivatives, BPOPT converges in 3 iterations with 1st and 2nd derivatives, and IPOPT converges in 2 iterations with 1st and 2nd derivatives.

(:source lang=python:) import matplotlib import numpy as np import matplotlib.pyplot as plt

1. define objective function

def f(x):

    x1 = x[0]
    x2 = x[1]
    obj = x1**2 - 2.0 * x1 * x2 + 4 * x2**2
    return obj

1. define objective gradient

def dfdx(x):

    x1 = x[0]
    x2 = x[1]
    grad = []
    grad.append(2.0 * x1 - 2.0 * x2)
    grad.append(-2.0 * x1 + 8.0 * x2)
    return grad

1. Exact 2nd derivatives (hessian)

H =

1. Start location

x_start = [-3.0, 2.0]

1. Design variables at mesh points

i1 = np.arange(-4.0, 4.0, 0.1) i2 = np.arange(-4.0, 4.0, 0.1) x1_mesh, x2_mesh = np.meshgrid(i1, i2) f_mesh = x1_mesh**2 - 2.0 * x1_mesh * x2_mesh + 4 * x2_mesh**2

1. Create a contour plot

plt.figure()

1. Specify contour lines

lines = range(2,52,2)

1. Plot contours

CS = plt.contour(x1_mesh, x2_mesh, f_mesh,lines)

1. Label contours

plt.clabel(CS, inline=1, fontsize=10)

1. Add some text to the plot

plt.title(r'$f(x)=x_1^2 - 2x_1x_2 + 4x_2^2$') plt.xlabel(r'$x_1$') plt.ylabel(r'$x_2$')

1. Newton's method

xn = np.zeros((2,2)) xn[0] = x_start

1. Get gradient at start location (df/dx or grad(f))

gn = dfdx(xn[0])

1. Compute search direction and magnitude (dx)
2. with dx = -inv(H) * grad

delta_xn = np.empty((1,2)) delta_xn = -np.linalg.solve(H,gn) xn[1] = xn[0]+delta_xn plt.plot(xn[:,0],xn[:,1],'k-o')

1. Steepest descent method

2. Number of iterations

n = 8

1. Use this alpha for every line search

alpha = 0.15

1. Initialize xs

xs = np.zeros((n+1,2)) xs[0] = x_start

1. Get gradient at start location (df/dx or grad(f))

for i in range(n):

    gs = dfdx(xs[i])
    # Compute search direction and magnitude (dx)
    #  with dx = - grad but no line searching
    xs[i+1] = xs[i] - np.dot(alpha,dfdx(xs[i]))

plt.plot(xs[:,0],xs[:,1],'g-o')

1. Conjugate gradient method

2. Number of iterations

n = 8

1. Use this alpha for the first line search

alpha = 0.15 neg =

1. Initialize xc

xc = np.zeros((n+1,2)) xc[0] = x_start

1. Initialize delta_gc

delta_cg = np.zeros((n+1,2))

1. Initialize gc

gc = np.zeros((n+1,2))

1. Get gradient at start location (df/dx or grad(f))

for i in range(n):

    gc[i] = dfdx(xc[i])
    # Compute search direction and magnitude (dx)
    #  with dx = - grad but no line searching
    if i==0:
        beta = 0
        delta_cg[i] = - np.dot(alpha,dfdx(xc[i]))
    else:
        beta = np.dot(gc[i],gc[i]) / np.dot(gc[i-1],gc[i-1])
        delta_cg[i] = alpha * np.dot(neg,dfdx(xc[i])) + beta * delta_cg[i-1]
    xc[i+1] = xc[i] + delta_cg[i] 

plt.plot(xc[:,0],xc[:,1],'y-o')

1. Quasi-Newton method

2. Number of iterations

n = 8

1. Use this alpha for every line search

alpha = np.linspace(0.1,1.0,n)

1. Initialize delta_xq and gamma

delta_xq = np.zeros((2,1)) gamma = np.zeros((2,1)) part1 = np.zeros((2,2)) part2 = np.zeros((2,2)) part3 = np.zeros((2,2)) part4 = np.zeros((2,2)) part5 = np.zeros((2,2)) part6 = np.zeros((2,1)) part7 = np.zeros((1,1)) part8 = np.zeros((2,2)) part9 = np.zeros((2,2))

1. Initialize xq

xq = np.zeros((n+1,2)) xq[0] = x_start

1. Initialize gradient storage

g = np.zeros((n+1,2)) g[0] = dfdx(xq[0])

1. Initialize hessian storage

h = np.zeros((n+1,2,2)) h[0] = for i in range(n):

    # Compute search direction and magnitude (dx)
    #  with dx = -alpha * inv(h) * grad
    delta_xq = -np.dot(alpha[i],np.linalg.solve(h[i],g[i]))
    xq[i+1] = xq[i] + delta_xq

    # Get gradient update for next step
    g[i+1] = dfdx(xq[i+1])

    # Get hessian update for next step
    gamma = g[i+1]-g[i]
    part1 = np.outer(gamma,gamma)
    part2 = np.outer(gamma,delta_xq)
    part3 = np.dot(np.linalg.pinv(part2),part1)

    part4 = np.outer(delta_xq,delta_xq)
    part5 = np.dot(h[i],part4)
    part6 = np.dot(part5,h[i])
    part7 = np.dot(delta_xq,h[i])
    part8 = np.dot(part7,delta_xq)
    part9 = np.dot(part6,1/part8)

    h[i+1] = h[i] + part3 - part9

plt.plot(xq[:,0],xq[:,1],'r-o') plt.savefig('contour.png') plt.show() (:sourceend:)

Search Direction Homework

Python Source: methods.py

(:html:) <!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.01//EN" "https://www.w3.org/TR/1999/REC-html401-19991224/strict.dtd"> <html> <head> <META http-equiv=Content-Type content="text/html; charset=UTF-8"> <title>Exported from Notepad++</title> <style type="text/css"> span {

	font-family: 'Courier New';
	font-size: 10pt;
	color: #000000;

} .sc0 { } .sc1 {

	color: #008000;

} .sc2 {

	color: #FF0000;

} .sc4 {

	color: #808080;

} .sc5 {

	font-weight: bold;
	color: #0000FF;

} .sc9 {

	color: #FF00FF;

} .sc10 {

	font-weight: bold;
	color: #000080;

} .sc11 { } .sc12 {

	color: #008000;

} </style> </head> <body> <div style="float: left; white-space: pre; line-height: 1; background: #FFFFFF; "><span class="sc12">## Generate a contour plot</span><span class="sc0"> </span><span class="sc1"># Import some other libraries that we'll need</span><span class="sc0"> </span><span class="sc1"># matplotlib and numpy packages must also be installed</span><span class="sc0"> </span><span class="sc5">import</span><span class="sc0"> </span><span class="sc11">matplotlib</span><span class="sc0"> </span><span class="sc5">import</span><span class="sc0"> </span><span class="sc11">numpy</span><span class="sc0"> </span><span class="sc5">as</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc0"> </span><span class="sc5">import</span><span class="sc0"> </span><span class="sc11">matplotlib</span><span class="sc10">.</span><span class="sc11">pyplot</span><span class="sc0"> </span><span class="sc5">as</span><span class="sc0"> </span><span class="sc11">plt</span><span class="sc0">

</span><span class="sc1"># define objective function</span><span class="sc0"> </span><span class="sc5">def</span><span class="sc0"> </span><span class="sc9">f</span><span class="sc10">(</span><span class="sc11">x</span><span class="sc10">):</span><span class="sc0">

    </span><span class="sc11">x1</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">x</span><span class="sc10">[</span><span class="sc2">0</span><span class="sc10">]</span><span class="sc0">
    </span><span class="sc11">x2</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">x</span><span class="sc10">[</span><span class="sc2">1</span><span class="sc10">]</span><span class="sc0">
    </span><span class="sc11">obj</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">x1</span><span class="sc10">**</span><span class="sc2">2</span><span class="sc0"> </span><span class="sc10">-</span><span class="sc0"> </span><span class="sc2">2.0</span><span class="sc0"> </span><span class="sc10">*</span><span class="sc0"> </span><span class="sc11">x1</span><span class="sc0"> </span><span class="sc10">*</span><span class="sc0"> </span><span class="sc11">x2</span><span class="sc0"> </span><span class="sc10">+</span><span class="sc0"> </span><span class="sc2">4</span><span class="sc0"> </span><span class="sc10">*</span><span class="sc0"> </span><span class="sc11">x2</span><span class="sc10">**</span><span class="sc2">2</span><span class="sc0">
    </span><span class="sc5">return</span><span class="sc0"> </span><span class="sc11">obj</span><span class="sc0">

</span><span class="sc1"># define objective gradient</span><span class="sc0"> </span><span class="sc5">def</span><span class="sc0"> </span><span class="sc9">dfdx</span><span class="sc10">(</span><span class="sc11">x</span><span class="sc10">):</span><span class="sc0">

    </span><span class="sc11">x1</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">x</span><span class="sc10">[</span><span class="sc2">0</span><span class="sc10">]</span><span class="sc0">
    </span><span class="sc11">x2</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">x</span><span class="sc10">[</span><span class="sc2">1</span><span class="sc10">]</span><span class="sc0">
    </span><span class="sc11">grad</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc10">[]</span><span class="sc0">
    </span><span class="sc11">grad</span><span class="sc10">.</span><span class="sc11">append</span><span class="sc10">(</span><span class="sc2">2.0</span><span class="sc0"> </span><span class="sc10">*</span><span class="sc0"> </span><span class="sc11">x1</span><span class="sc0"> </span><span class="sc10">-</span><span class="sc0"> </span><span class="sc2">2.0</span><span class="sc0"> </span><span class="sc10">*</span><span class="sc0"> </span><span class="sc11">x2</span><span class="sc10">)</span><span class="sc0">
    </span><span class="sc11">grad</span><span class="sc10">.</span><span class="sc11">append</span><span class="sc10">(-</span><span class="sc2">2.0</span><span class="sc0"> </span><span class="sc10">*</span><span class="sc0"> </span><span class="sc11">x1</span><span class="sc0"> </span><span class="sc10">+</span><span class="sc0"> </span><span class="sc2">8.0</span><span class="sc0"> </span><span class="sc10">*</span><span class="sc0"> </span><span class="sc11">x2</span><span class="sc10">)</span><span class="sc0">
    </span><span class="sc5">return</span><span class="sc0"> </span><span class="sc11">grad</span><span class="sc0">

</span><span class="sc1"># Exact 2nd derivatives (hessian)</span><span class="sc0"> </span><span class="sc11">H</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc10"></span><span class="sc0">

</span><span class="sc1"># Start location</span><span class="sc0"> </span><span class="sc11">x_start</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc10">[-</span><span class="sc2">3.0</span><span class="sc10">,</span><span class="sc0"> </span><span class="sc2">2.0</span><span class="sc10">]</span><span class="sc0">

</span><span class="sc1"># Design variables at mesh points</span><span class="sc0"> </span><span class="sc11">i1</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">arange</span><span class="sc10">(-</span><span class="sc2">4.0</span><span class="sc10">,</span><span class="sc0"> </span><span class="sc2">4.0</span><span class="sc10">,</span><span class="sc0"> </span><span class="sc2">0.1</span><span class="sc10">)</span><span class="sc0"> </span><span class="sc11">i2</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">arange</span><span class="sc10">(-</span><span class="sc2">4.0</span><span class="sc10">,</span><span class="sc0"> </span><span class="sc2">4.0</span><span class="sc10">,</span><span class="sc0"> </span><span class="sc2">0.1</span><span class="sc10">)</span><span class="sc0"> </span><span class="sc11">x1_mesh</span><span class="sc10">,</span><span class="sc0"> </span><span class="sc11">x2_mesh</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">meshgrid</span><span class="sc10">(</span><span class="sc11">i1</span><span class="sc10">,</span><span class="sc0"> </span><span class="sc11">i2</span><span class="sc10">)</span><span class="sc0"> </span><span class="sc11">f_mesh</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">x1_mesh</span><span class="sc10">**</span><span class="sc2">2</span><span class="sc0"> </span><span class="sc10">-</span><span class="sc0"> </span><span class="sc2">2.0</span><span class="sc10">*</span><span class="sc11">x1_mesh</span><span class="sc10">*</span><span class="sc11">x2_mesh</span><span class="sc0"> </span><span class="sc10">+</span><span class="sc0"> </span><span class="sc2">4.0</span><span class="sc10">*</span><span class="sc11">x2_mesh</span><span class="sc10">**</span><span class="sc2">2</span><span class="sc0">

</span><span class="sc1"># Create a contour plot</span><span class="sc0"> </span><span class="sc11">plt</span><span class="sc10">.</span><span class="sc11">figure</span><span class="sc10">()</span><span class="sc0"> </span><span class="sc1"># Specify contour lines</span><span class="sc0"> </span><span class="sc11">lines</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">range</span><span class="sc10">(</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">52</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">)</span><span class="sc0"> </span><span class="sc1"># Plot contours</span><span class="sc0"> </span><span class="sc11">CS</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">plt</span><span class="sc10">.</span><span class="sc11">contour</span><span class="sc10">(</span><span class="sc11">x1_mesh</span><span class="sc10">,</span><span class="sc0"> </span><span class="sc11">x2_mesh</span><span class="sc10">,</span><span class="sc0"> </span><span class="sc11">f_mesh</span><span class="sc10">,</span><span class="sc11">lines</span><span class="sc10">)</span><span class="sc0"> </span><span class="sc1"># Label contours</span><span class="sc0"> </span><span class="sc11">plt</span><span class="sc10">.</span><span class="sc11">clabel</span><span class="sc10">(</span><span class="sc11">CS</span><span class="sc10">,</span><span class="sc0"> </span><span class="sc11">inline</span><span class="sc10">=</span><span class="sc2">1</span><span class="sc10">,</span><span class="sc0"> </span><span class="sc11">fontsize</span><span class="sc10">=</span><span class="sc2">10</span><span class="sc10">)</span><span class="sc0"> </span><span class="sc1"># Add some text to the plot</span><span class="sc0"> </span><span class="sc11">plt</span><span class="sc10">.</span><span class="sc11">title</span><span class="sc10">(</span><span class="sc4">'f(x) = x1^2 - 2*x1*x2 + 4*x2^2'</span><span class="sc10">)</span><span class="sc0"> </span><span class="sc11">plt</span><span class="sc10">.</span><span class="sc11">xlabel</span><span class="sc10">(</span><span class="sc4">'x1'</span><span class="sc10">)</span><span class="sc0"> </span><span class="sc11">plt</span><span class="sc10">.</span><span class="sc11">ylabel</span><span class="sc10">(</span><span class="sc4">'x2'</span><span class="sc10">)</span><span class="sc0"> </span><span class="sc1"># Show the plot</span><span class="sc0"> </span><span class="sc1">#plt.show()</span><span class="sc0">

</span><span class="sc12">##################################################</span><span class="sc0"> </span><span class="sc1"># Newton's method</span><span class="sc0"> </span><span class="sc12">##################################################</span><span class="sc0"> </span><span class="sc11">xn</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">xn</span><span class="sc10">[</span><span class="sc2">0</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">x_start</span><span class="sc0"> </span><span class="sc1"># Get gradient at start location (df/dx or grad(f))</span><span class="sc0"> </span><span class="sc11">gn</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">dfdx</span><span class="sc10">(</span><span class="sc11">xn</span><span class="sc10">[</span><span class="sc2">0</span><span class="sc10">])</span><span class="sc0"> </span><span class="sc1"># Compute search direction and magnitude (dx)</span><span class="sc0"> </span><span class="sc1"># with dx = -inv(H) * grad</span><span class="sc0"> </span><span class="sc11">delta_xn</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">empty</span><span class="sc10">((</span><span class="sc2">1</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">delta_xn</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc10">-</span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">linalg</span><span class="sc10">.</span><span class="sc11">solve</span><span class="sc10">(</span><span class="sc11">H</span><span class="sc10">,</span><span class="sc11">gn</span><span class="sc10">)</span><span class="sc0"> </span><span class="sc11">xn</span><span class="sc10">[</span><span class="sc2">1</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">xn</span><span class="sc10">[</span><span class="sc2">0</span><span class="sc10">]+</span><span class="sc11">delta_xn</span><span class="sc0"> </span><span class="sc11">plt</span><span class="sc10">.</span><span class="sc11">plot</span><span class="sc10">(</span><span class="sc11">xn</span><span class="sc10">[:,</span><span class="sc2">0</span><span class="sc10">],</span><span class="sc11">xn</span><span class="sc10">[:,</span><span class="sc2">1</span><span class="sc10">],</span><span class="sc4">'k-o'</span><span class="sc10">)</span><span class="sc0">

</span><span class="sc12">##################################################</span><span class="sc0"> </span><span class="sc1"># Steepest descent method</span><span class="sc0"> </span><span class="sc12">##################################################</span><span class="sc0"> </span><span class="sc1"># Number of iterations</span><span class="sc0"> </span><span class="sc11">n</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc2">8</span><span class="sc0"> </span><span class="sc1"># Use this alpha for every line search</span><span class="sc0"> </span><span class="sc11">alpha</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc2">0.15</span><span class="sc0"> </span><span class="sc1"># Initialize xs</span><span class="sc0"> </span><span class="sc11">xs</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc11">n</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">xs</span><span class="sc10">[</span><span class="sc2">0</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">x_start</span><span class="sc0"> </span><span class="sc1"># Get gradient at start location (df/dx or grad(f))</span><span class="sc0"> </span><span class="sc5">for</span><span class="sc0"> </span><span class="sc11">i</span><span class="sc0"> </span><span class="sc5">in</span><span class="sc0"> </span><span class="sc11">range</span><span class="sc10">(</span><span class="sc11">n</span><span class="sc10">):</span><span class="sc0">

    </span><span class="sc11">gs</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">dfdx</span><span class="sc10">(</span><span class="sc11">xs</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">])</span><span class="sc0">
    </span><span class="sc1"># Compute search direction and magnitude (dx)</span><span class="sc0">
    </span><span class="sc1">#  with dx = - grad but no line searching</span><span class="sc0">
    </span><span class="sc11">xs</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">xs</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">-</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">dot</span><span class="sc10">(</span><span class="sc11">alpha</span><span class="sc10">,</span><span class="sc11">dfdx</span><span class="sc10">(</span><span class="sc11">xs</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]))</span><span class="sc0">

</span><span class="sc11">plt</span><span class="sc10">.</span><span class="sc11">plot</span><span class="sc10">(</span><span class="sc11">xs</span><span class="sc10">[:,</span><span class="sc2">0</span><span class="sc10">],</span><span class="sc11">xs</span><span class="sc10">[:,</span><span class="sc2">1</span><span class="sc10">],</span><span class="sc4">'g-o'</span><span class="sc10">)</span><span class="sc0">

</span><span class="sc12">##################################################</span><span class="sc0"> </span><span class="sc1"># Conjugate gradient method</span><span class="sc0"> </span><span class="sc12">##################################################</span><span class="sc0"> </span><span class="sc1"># Number of iterations</span><span class="sc0"> </span><span class="sc11">n</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc2">8</span><span class="sc0"> </span><span class="sc1"># Use this alpha for the first line search</span><span class="sc0"> </span><span class="sc11">alpha</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc2">0.15</span><span class="sc0"> </span><span class="sc11">neg</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc10"></span><span class="sc0"> </span><span class="sc1"># Initialize xc</span><span class="sc0"> </span><span class="sc11">xc</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc11">n</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">xc</span><span class="sc10">[</span><span class="sc2">0</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">x_start</span><span class="sc0"> </span><span class="sc1"># Initialize delta_gc</span><span class="sc0"> </span><span class="sc11">delta_cg</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc11">n</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc1"># Initialize gc</span><span class="sc0"> </span><span class="sc11">gc</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc11">n</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc1"># Get gradient at start location (df/dx or grad(f))</span><span class="sc0"> </span><span class="sc5">for</span><span class="sc0"> </span><span class="sc11">i</span><span class="sc0"> </span><span class="sc5">in</span><span class="sc0"> </span><span class="sc11">range</span><span class="sc10">(</span><span class="sc11">n</span><span class="sc10">):</span><span class="sc0">

    </span><span class="sc11">gc</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">dfdx</span><span class="sc10">(</span><span class="sc11">xc</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">])</span><span class="sc0">
    </span><span class="sc1"># Compute search direction and magnitude (dx)</span><span class="sc0">
    </span><span class="sc1">#  with dx = - grad but no line searching</span><span class="sc0">
    </span><span class="sc5">if</span><span class="sc0"> </span><span class="sc11">i</span><span class="sc10">==</span><span class="sc2">0</span><span class="sc10">:</span><span class="sc0">
        </span><span class="sc11">beta</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc2">0</span><span class="sc0">
        </span><span class="sc11">delta_cg</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc10">-</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">dot</span><span class="sc10">(</span><span class="sc11">alpha</span><span class="sc10">,</span><span class="sc11">dfdx</span><span class="sc10">(</span><span class="sc11">xc</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]))</span><span class="sc0">
    </span><span class="sc5">else</span><span class="sc10">:</span><span class="sc0">
        </span><span class="sc11">beta</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">dot</span><span class="sc10">(</span><span class="sc11">gc</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">],</span><span class="sc11">gc</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">])</span><span class="sc0"> </span><span class="sc10">/</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">dot</span><span class="sc10">(</span><span class="sc11">gc</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">-</span><span class="sc2">1</span><span class="sc10">],</span><span class="sc11">gc</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">-</span><span class="sc2">1</span><span class="sc10">])</span><span class="sc0">
        </span><span class="sc11">delta_cg</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">alpha</span><span class="sc0"> </span><span class="sc10">*</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">dot</span><span class="sc10">(</span><span class="sc11">neg</span><span class="sc10">,</span><span class="sc11">dfdx</span><span class="sc10">(</span><span class="sc11">xc</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]))</span><span class="sc0">             </span><span class="sc10">+</span><span class="sc0"> </span><span class="sc11">beta</span><span class="sc0"> </span><span class="sc10">*</span><span class="sc0"> </span><span class="sc11">delta_cg</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">-</span><span class="sc2">1</span><span class="sc10">]</span><span class="sc0">
    </span><span class="sc11">xc</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">xc</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">+</span><span class="sc0"> </span><span class="sc11">delta_cg</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]</span><span class="sc0"> 

</span><span class="sc11">plt</span><span class="sc10">.</span><span class="sc11">plot</span><span class="sc10">(</span><span class="sc11">xc</span><span class="sc10">[:,</span><span class="sc2">0</span><span class="sc10">],</span><span class="sc11">xc</span><span class="sc10">[:,</span><span class="sc2">1</span><span class="sc10">],</span><span class="sc4">'y-o'</span><span class="sc10">)</span><span class="sc0">

</span><span class="sc12">##################################################</span><span class="sc0"> </span><span class="sc1"># Quasi-Newton method</span><span class="sc0"> </span><span class="sc12">##################################################</span><span class="sc0"> </span><span class="sc1"># Number of iterations</span><span class="sc0"> </span><span class="sc11">n</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc2">8</span><span class="sc0"> </span><span class="sc1"># Use this alpha for every line search</span><span class="sc0"> </span><span class="sc11">alpha</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">linspace</span><span class="sc10">(</span><span class="sc2">0.1</span><span class="sc10">,</span><span class="sc2">1.0</span><span class="sc10">,</span><span class="sc11">n</span><span class="sc10">)</span><span class="sc0"> </span><span class="sc1"># Initialize delta_xq and gamma</span><span class="sc0"> </span><span class="sc11">delta_xq</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">1</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">gamma</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">1</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">part1</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">part2</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">part3</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">part4</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">part5</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">part6</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">1</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">part7</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc2">1</span><span class="sc10">,</span><span class="sc2">1</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">part8</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">part9</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc1"># Initialize xq</span><span class="sc0"> </span><span class="sc11">xq</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc11">n</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">xq</span><span class="sc10">[</span><span class="sc2">0</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">x_start</span><span class="sc0"> </span><span class="sc1"># Initialize gradient storage</span><span class="sc0"> </span><span class="sc11">g</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc11">n</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">g</span><span class="sc10">[</span><span class="sc2">0</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">dfdx</span><span class="sc10">(</span><span class="sc11">xq</span><span class="sc10">[</span><span class="sc2">0</span><span class="sc10">])</span><span class="sc0"> </span><span class="sc1"># Initialize hessian storage</span><span class="sc0"> </span><span class="sc11">h</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">zeros</span><span class="sc10">((</span><span class="sc11">n</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">,</span><span class="sc2">2</span><span class="sc10">))</span><span class="sc0"> </span><span class="sc11">h</span><span class="sc10">[</span><span class="sc2">0</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc10"></span><span class="sc0"> </span><span class="sc5">for</span><span class="sc0"> </span><span class="sc11">i</span><span class="sc0"> </span><span class="sc5">in</span><span class="sc0"> </span><span class="sc11">range</span><span class="sc10">(</span><span class="sc11">n</span><span class="sc10">):</span><span class="sc0">

    </span><span class="sc1"># Compute search direction and magnitude (dx)</span><span class="sc0">
    </span><span class="sc1">#  with dx = -alpha * inv(h) * grad</span><span class="sc0">
    </span><span class="sc11">delta_xq</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc10">-</span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">dot</span><span class="sc10">(</span><span class="sc11">alpha</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">],</span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">linalg</span><span class="sc10">.</span><span class="sc11">solve</span><span class="sc10">(</span><span class="sc11">h</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">],</span><span class="sc11">g</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]))</span><span class="sc0">
    </span><span class="sc11">xq</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">xq</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">+</span><span class="sc0"> </span><span class="sc11">delta_xq</span><span class="sc0">

    </span><span class="sc1"># Get gradient update for next step</span><span class="sc0">
    </span><span class="sc11">g</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">dfdx</span><span class="sc10">(</span><span class="sc11">xq</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">])</span><span class="sc0">

    </span><span class="sc1"># Get hessian update for next step</span><span class="sc0">
    </span><span class="sc11">gamma</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">g</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">]-</span><span class="sc11">g</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]</span><span class="sc0">
    </span><span class="sc11">part1</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">outer</span><span class="sc10">(</span><span class="sc11">gamma</span><span class="sc10">,</span><span class="sc11">gamma</span><span class="sc10">)</span><span class="sc0">
    </span><span class="sc11">part2</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">outer</span><span class="sc10">(</span><span class="sc11">gamma</span><span class="sc10">,</span><span class="sc11">delta_xq</span><span class="sc10">)</span><span class="sc0">
    </span><span class="sc11">part3</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">dot</span><span class="sc10">(</span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">linalg</span><span class="sc10">.</span><span class="sc11">pinv</span><span class="sc10">(</span><span class="sc11">part2</span><span class="sc10">),</span><span class="sc11">part1</span><span class="sc10">)</span><span class="sc0">

    </span><span class="sc11">part4</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">outer</span><span class="sc10">(</span><span class="sc11">delta_xq</span><span class="sc10">,</span><span class="sc11">delta_xq</span><span class="sc10">)</span><span class="sc0">
    </span><span class="sc11">part5</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">dot</span><span class="sc10">(</span><span class="sc11">h</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">],</span><span class="sc11">part4</span><span class="sc10">)</span><span class="sc0">
    </span><span class="sc11">part6</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">dot</span><span class="sc10">(</span><span class="sc11">part5</span><span class="sc10">,</span><span class="sc11">h</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">])</span><span class="sc0">
    </span><span class="sc11">part7</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">dot</span><span class="sc10">(</span><span class="sc11">delta_xq</span><span class="sc10">,</span><span class="sc11">h</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">])</span><span class="sc0">
    </span><span class="sc11">part8</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">dot</span><span class="sc10">(</span><span class="sc11">part7</span><span class="sc10">,</span><span class="sc11">delta_xq</span><span class="sc10">)</span><span class="sc0">
    </span><span class="sc11">part9</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">np</span><span class="sc10">.</span><span class="sc11">dot</span><span class="sc10">(</span><span class="sc11">part6</span><span class="sc10">,</span><span class="sc2">1</span><span class="sc10">/</span><span class="sc11">part8</span><span class="sc10">)</span><span class="sc0">

    </span><span class="sc11">h</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">+</span><span class="sc2">1</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">=</span><span class="sc0"> </span><span class="sc11">h</span><span class="sc10">[</span><span class="sc11">i</span><span class="sc10">]</span><span class="sc0"> </span><span class="sc10">+</span><span class="sc0"> </span><span class="sc11">part3</span><span class="sc0"> </span><span class="sc10">-</span><span class="sc0"> </span><span class="sc11">part9</span><span class="sc0">

</span><span class="sc11">plt</span><span class="sc10">.</span><span class="sc11">plot</span><span class="sc10">(</span><span class="sc11">xq</span><span class="sc10">[:,</span><span class="sc2">0</span><span class="sc10">],</span><span class="sc11">xq</span><span class="sc10">[:,</span><span class="sc2">1</span><span class="sc10">],</span><span class="sc4">'r-o'</span><span class="sc10">)</span><span class="sc0">

</span><span class="sc1"># Save the figure as a PNG</span><span class="sc0"> </span><span class="sc11">plt</span><span class="sc10">.</span><span class="sc11">savefig</span><span class="sc10">(</span><span class="sc4">'contour.png'</span><span class="sc10">)</span><span class="sc0">

</span><span class="sc11">plt</span><span class="sc10">.</span><span class="sc11">show</span><span class="sc10">()</span><span class="sc0"> </span></div></body> </html> (:htmlend:)

MATLAB Source Code

• Methods for Obtaining Search Directions (search_methods_matlab.zip)

Search Direction Worksheet

Search Direction Worksheet

Python Source Code

(:title Quasi Newton Methods in Optimization:) (:keywords quasi-newton, optimization, nonlinear programming:) (:description Exercise on Quasi-Newton approximations and code examples for solving simple problems.:)

Quasi-Newton Approximations

The following exercise demonstrates the use of Quasi-Newton methods, Newton's methods, and a Steepest Descent approach to unconstrained optimization. The following tutorial covers:

• Newton's method (exact 2nd derivatives)
• BFGS-Update method (approximate 2nd derivatives)
• Conjugate gradient method
• Steepest descent method

Chapter 3 covers each of these methods and the theoretical background for each. The following exercise is a practical implementation of each method with simplified example code for instructional purposes. The examples do not perform line searching which will be covered in more detail later.

• Methods for Obtaining Search Directions (search_direction_methods.zip)

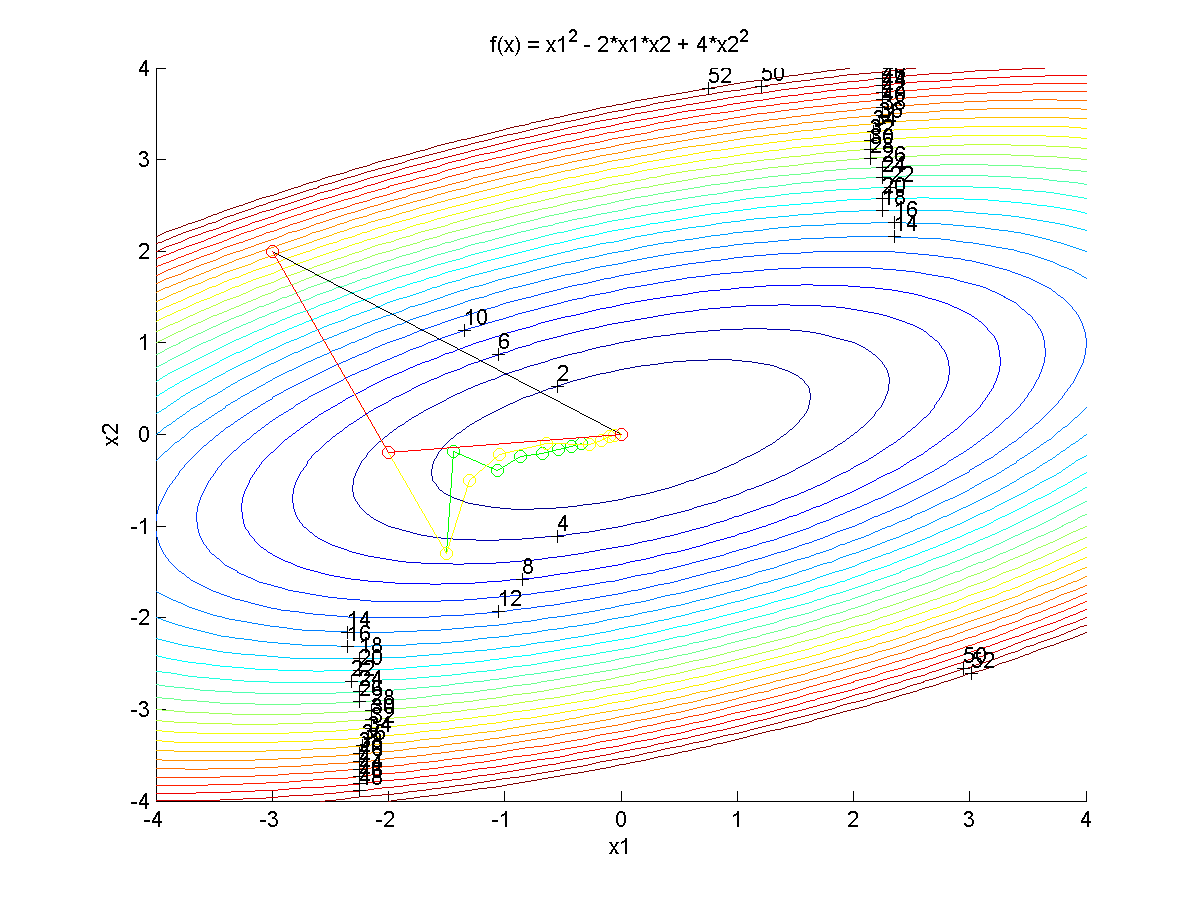
(:html:) <iframe width="640" height="360" src="https://www.youtube.com/embed/mLYpktmbLZw?rel=0" frameborder="0" allowfullscreen></iframe> (:htmlend:)

(:html:)

 <div id="disqus_thread"></div>
    <script type="text/javascript">
        /* * * CONFIGURATION VARIABLES: EDIT BEFORE PASTING INTO YOUR WEBPAGE * * */
        var disqus_shortname = 'apmonitor'; // required: replace example with your forum shortname

        /* * * DON'T EDIT BELOW THIS LINE * * */
        (function() {
            var dsq = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
            dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
            (document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(dsq);
        })();
    </script>
    <noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
    <a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>

(:htmlend:)