Design Optimization

import threading
import datetime
import time, random

class MyThread(threading.Thread):
    def __init__(self, id):
        self.id = id
        self.delay = random.random()
        threading.Thread.__init__(self)
    def run(self):
        time.sleep(self.delay)
        now = datetime.datetime.now()
        print("ID => %s: %s completes at %s\n" % \
              (self.id, self.getName(), now))

# Start threads
threads = []
for i in range(10):
    threads.append(MyThread(i))
    threads[i].start()
    print('Active threads: ' + str(threading.activeCount()))

# Print threads
print('All threads: \n')
print(threading.enumerate())

# Wait for all threads to complete
for t in threads:
    t.join()
print('Threads complete')

import numpy as np
from gekko import GEKKO

# Optimize at mesh points
x = np.arange(20.0, 30.0, 2.0)
y = np.arange(30.0, 50.0, 4.0)
amg, bmg = np.meshgrid(x, y)

# Initialize results array
obj = np.empty_like(amg)

m = GEKKO(remote=False)
objective = float('NaN')

a,b = m.Array(m.FV,2)

# model variables, equations, objective
x1 = m.Var(1,lb=1,ub=5)
x2 = m.Var(5,lb=1,ub=5)
x3 = m.Var(5,lb=1,ub=5)
x4 = m.Var(1,lb=1,ub=5)
m.Equation(x1*x2*x3*x4>=a)
m.Equation(x1**2+x2**2+x3**2+x4**2==b)
m.Minimize(x1*x4*(x1+x2+x3)+x3)
m.options.SOLVER = 1 # APOPT solver

# Calculate obj at all meshgrid points
for i in range(amg.shape[0]):
    for j in range(bmg.shape[1]):
        a.MEAS = amg[i,j]
        b.MEAS = bmg[i,j]

        m.solve(disp=False)

        obj[i,j] = m.options.OBJFCNVAL
        print(amg[i,j],bmg[i,j],obj[i,j])

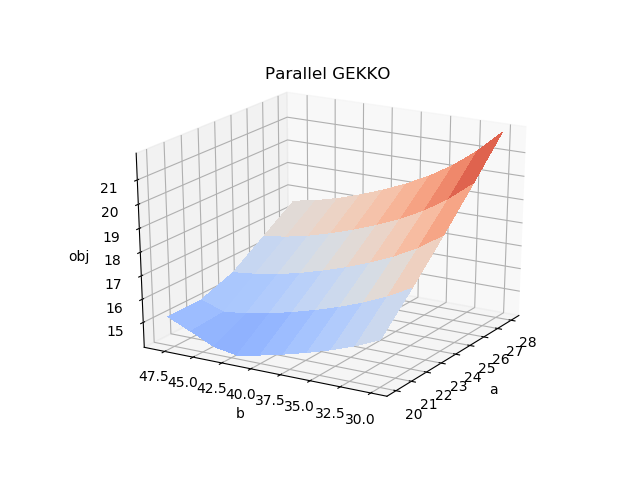
# plot 3D figure of results
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import cm
import numpy as np

fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(amg, bmg, obj, \
       rstride=1, cstride=1, cmap=cm.coolwarm, \
       vmin = 10, vmax = 25, linewidth=0, antialiased=False)
ax.set_xlabel('a')
ax.set_ylabel('b')
ax.set_zlabel('obj')
plt.show()

import numpy as np
import threading
import time, random
from gekko import GEKKO

class ThreadClass(threading.Thread):
    def __init__(self, id, server, ai, bi):
        s = self
        s.id = id
        s.server = server
        s.m = GEKKO(remote=False)
        s.a = ai
        s.b = bi
        s.objective = float('NaN')

        # initialize variables
        s.m.x1 = s.m.Var(1,lb=1,ub=5)
        s.m.x2 = s.m.Var(5,lb=1,ub=5)
        s.m.x3 = s.m.Var(5,lb=1,ub=5)
        s.m.x4 = s.m.Var(1,lb=1,ub=5)

        # Equations
        s.m.Equation(s.m.x1*s.m.x2*s.m.x3*s.m.x4>=s.a)
        s.m.Equation(s.m.x1**2+s.m.x2**2+s.m.x3**2+s.m.x4**2==s.b)

        # Objective
        s.m.Minimize(s.m.x1*s.m.x4*(s.m.x1+s.m.x2+s.m.x3)+s.m.x3)

        # Set global options
        s.m.options.IMODE = 3 # steady state optimization
        s.m.options.SOLVER = 1 # APOPT solver

        threading.Thread.__init__(s)

    def run(self):

        # Don't overload server by executing all scripts at once
        sleep_time = random.random()
        time.sleep(sleep_time)

        print('Running application ' + str(self.id) + '\n')

        # Solve
        self.m.solve(disp=False)

        # Results
        #print('')
        #print('Results')
        #print('x1: ' + str(self.m.x1.value))
        #print('x2: ' + str(self.m.x2.value))
        #print('x3: ' + str(self.m.x3.value))
        #print('x4: ' + str(self.m.x4.value))

        # Retrieve objective if successful
        if (self.m.options.APPSTATUS==1):
            self.objective = self.m.options.objfcnval
        else:
            self.objective = float('NaN')
        self.m.cleanup()

# Select server
server = 'https://byu.apmonitor.com'

# Optimize at mesh points
x = np.arange(20.0, 30.0, 2.0)
y = np.arange(30.0, 50.0, 2.0)
a, b = np.meshgrid(x, y)

# Array of threads
threads = []

# Calculate objective at all meshgrid points

# Load applications
id = 0
for i in range(a.shape[0]):
    for j in range(b.shape[1]):
        # Create new thread
        threads.append(ThreadClass(id, server, a[i,j], b[i,j]))
        # Increment ID
        id += 1

# Run applications simultaneously as multiple threads
# Max number of threads to run at once
max_threads = 8
for t in threads:
    while (threading.activeCount()>max_threads):
        # check for additional threads every 0.01 sec
        time.sleep(0.01)
    # start the thread
    t.start()

# Check for completion
mt = 3.0 # max time
it = 0.0 # incrementing time
st = 1.0 # sleep time
while (threading.activeCount()>=1):
    time.sleep(st)
    it = it + st
    print('Active Threads: ' + str(threading.activeCount()))
    # Terminate after max time
    if (it>=mt):
        break

# Wait for all threads to complete
#for t in threads:
#    t.join()
#print('Threads complete')

# Initialize array for objective
obj = np.empty_like(a)

# Retrieve objective results
id = 0
for i in range(a.shape[0]):
    for j in range(b.shape[1]):
        obj[i,j] = threads[id].objective
        id += 1

# plot 3D figure of results
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import cm
import numpy as np

fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(a, b, obj, \
                       rstride=1, cstride=1, cmap=cm.coolwarm, \
                       vmin = 12, vmax = 22, linewidth=0, antialiased=False)
ax.set_xlabel('a')
ax.set_ylabel('b')
ax.set_zlabel('obj')
ax.set_title('Multi-Threaded GEKKO')
plt.show()