Dynamic Estimation
Dynamic estimation involves fitting parameters in a dynamic model. In many cases, a linear first order differential equation can approximate the dynamic evolution of many systems. The unknown parameters for this system include the time constant (tau), gain (K), and sometimes dead-time (theta).
For this exercise, you can assume that the dead-time (theta) is zero and estimate only the time constant (tau) and gain (K). The following data set was generated in class from a voltage input (u) that changed the temperature (x) of a thermister.
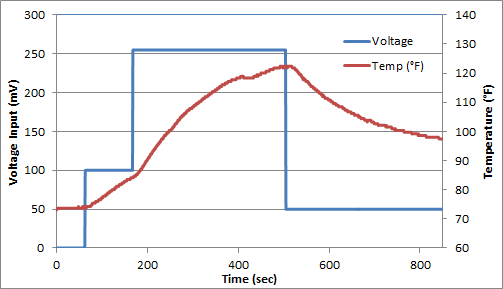
Fit the dynamic data to a first order linear system by estimating tau (time constant) and K (gain). Determine the 95% and 99% confidence intervals for the parameters (see F-test video tutorial).
Excel Solution
The dynamic model can be written in discrete form by specifying that the voltage is constant between sampling intervals. The discrete form of the equation accounts for non-zero initial conditions in temperature (x0) and voltage (u0). In this case, the voltage does start at zero, but this is not required.
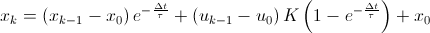
In this equation, the subscripts denote the sampling intervals that are collected at a time interval of delta time = tk-tk-1. The above equation and the data are put into an Excel worksheet. The difference between the measured and predicted values are minimized to obtain the optimal parameters K (gain) and tau (time constant).
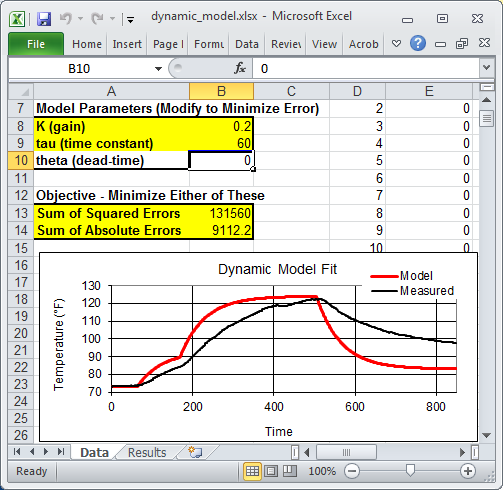
The spreadsheet is currently showing non-optimal values. To obtain the optimal values, use Excel Solver available from the Data toolbar. If the solver option does not appear, it can be added with the Add-In manager.
MATLAB and Python Solutions
An alternative approach to the sum of squared errors is to minimize an L1-norm error to find the optimal values of K (gain) and tau (time constant).
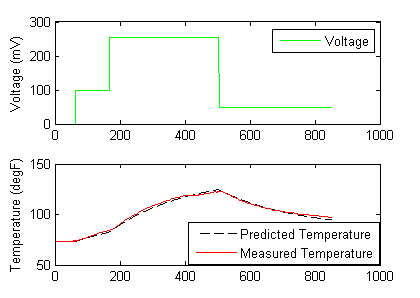
The required Python packages are Python, Numpy, Matplotlib, and Scipy. The MATLAB and Python plots produce trends that show the optimal solution with an l1-norm objective function.
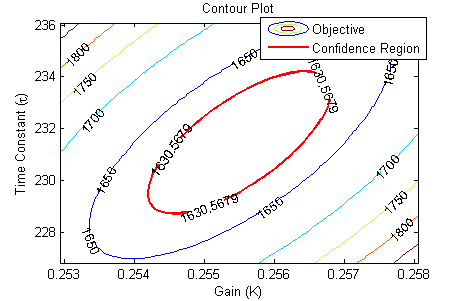
The nonlinear confidence interval is shown by producing a contour plot of the SSE objective function with variations in the two parameters. The optimal solution is shown at the center of the plot and the objective function becomes worse (higher) away from the optimal solution.
The confidence interval is determined with an F-test that specifies an upper limit to the deviation from the optimal solution
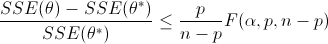
with p=2 (number of parameters), n=851 (number of measurements), theta=[K,tau] (parameters), theta* as the optimal parameters, SSE as the sum of squared errors, and the F statistic that has 3 arguments (alpha=confidence level, degrees of freedom 1, and degrees of freedom 2). For many problems, this creates a multi-dimensional nonlinear confidence region. In the case of 2 parameters, the nonlinear confidence region is a 2-dimensional space.
The difficulty of the last few assignments has been reduced to allow time for work on the Final Project. Please use the additional time this week to develop the project and start the write-up.
This assignment can be completed in groups of two. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.