Quasi Newton Methods in Optimization

Quasi-Newton methods are a class of numerical optimization algorithms that are used to find minima or maxima of functions. They are a generalization of Newton's method, which uses the Hessian matrix of second derivatives to approximate the local curvature of a function. Quasi-Newton methods use approximate versions of the Hessian matrix that are updated as the algorithm proceeds. This allows the algorithm to more quickly converge to the optimum without needing to compute the full Hessian matrix. The most commonly used quasi-Newton methods are the Broyden–Fletcher–Goldfarb–Shanno (BFGS) and the limited memory BFGS (L-BFGS).

The following exercise demonstrates the use of Quasi-Newton methods, Newton's methods, and a Steepest Descent approach to unconstrained optimization. The following tutorial covers:

Newton's method (exact 2nd derivatives)
BFGS-Update method (approximate 2nd derivatives)
Conjugate gradient method
Steepest descent method

Search Direction Homework

Chapter 3 covers each of these methods and the theoretical background for each. The following exercise is a practical implementation of each method with simplified example code for instructional purposes. The examples do not perform line searching which will be covered in more detail later.

MATLAB Source Code

 Newton's method
 Steepest descent
 Conjugate gradient
 BFGS update

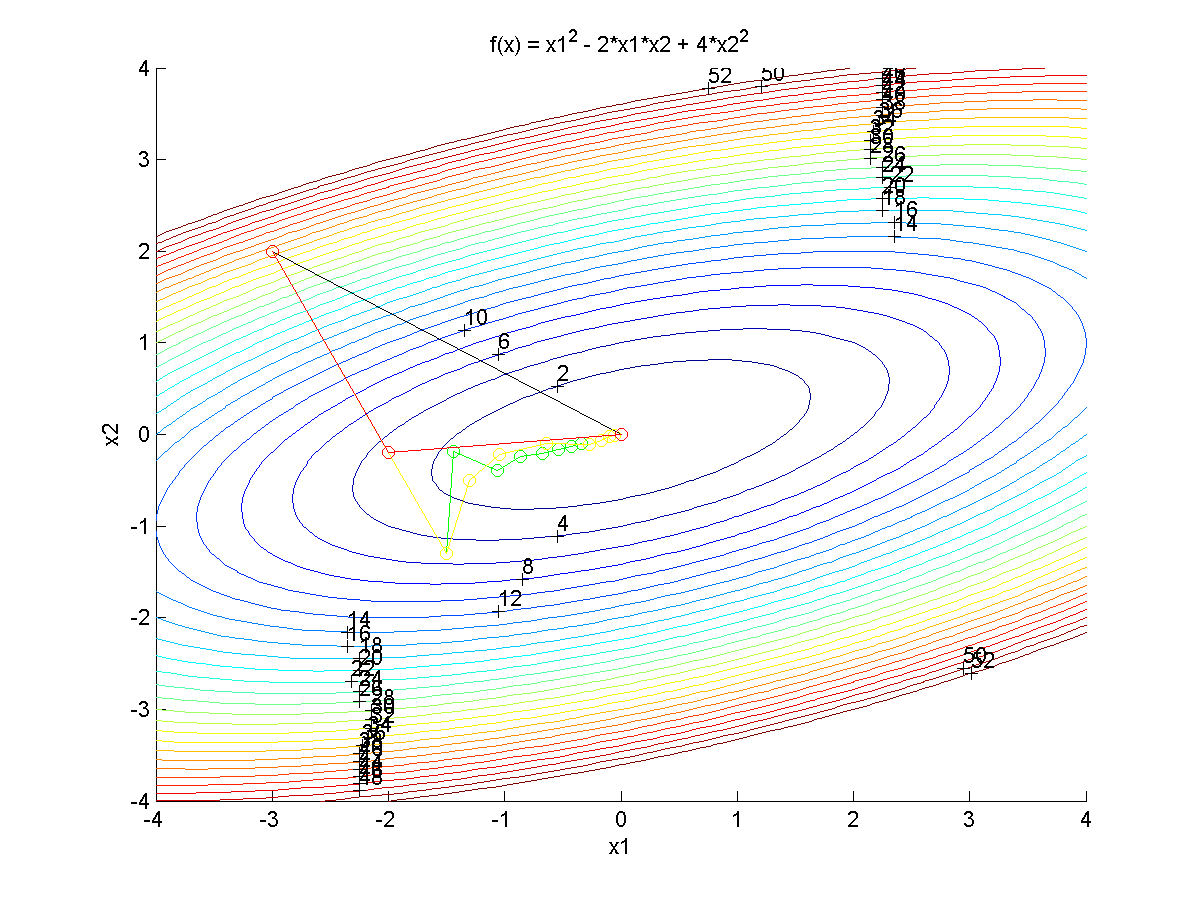
Methods for Obtaining Search Directions (search_methods_matlab.zip)

Python Source Code

 Newton's method
 Steepest descent
 Conjugate gradient
 BFGS update

import matplotlib
import numpy as np
import matplotlib.pyplot as plt

# define objective function
def f(x):
x1 = x[0]
x2 = x[1]
obj = x1**2 - 2.0 * x1 * x2 + 4 * x2**2
return obj

# define objective gradient
def dfdx(x):
x1 = x[0]
x2 = x[1]
grad = []
grad.append(2.0 * x1 - 2.0 * x2)
grad.append(-2.0 * x1 + 8.0 * x2)
return grad

# Exact 2nd derivatives (hessian)
H = [[2.0, -2.0],[-2.0, 8.0]]

# Start location
x_start = [-3.0, 2.0]

# Design variables at mesh points
i1 = np.arange(-4.0, 4.0, 0.1)
i2 = np.arange(-4.0, 4.0, 0.1)
x1_mesh, x2_mesh = np.meshgrid(i1, i2)
f_mesh = x1_mesh**2 - 2.0 * x1_mesh * x2_mesh + 4 * x2_mesh**2

# Create a contour plot
plt.figure()
# Specify contour lines
lines = range(2,52,2)
# Plot contours
CS = plt.contour(x1_mesh, x2_mesh, f_mesh,lines)
# Label contours
plt.clabel(CS, inline=1, fontsize=10)
# Add some text to the plot
plt.title(r'$f(x)=x_1^2 - 2x_1x_2 + 4x_2^2$')
plt.xlabel(r'$x_1$')
plt.ylabel(r'$x_2$')

##################################################
# Newton's method
##################################################
xn = np.zeros((2,2))
xn[0] = x_start
# Get gradient at start location (df/dx or grad(f))
gn = dfdx(xn[0])
# Compute search direction and magnitude (dx)
# with dx = -inv(H) * grad
delta_xn = np.empty((1,2))
delta_xn = -np.linalg.solve(H,gn)
xn[1] = xn[0]+delta_xn
plt.plot(xn[:,0],xn[:,1],'k-o')

##################################################
# Steepest descent method
##################################################
# Number of iterations
n = 8
# Use this alpha for every line search
alpha = 0.15
# Initialize xs
xs = np.zeros((n+1,2))
xs[0] = x_start
# Get gradient at start location (df/dx or grad(f))
for i in range(n):
gs = dfdx(xs[i])
# Compute search direction and magnitude (dx)
# with dx = - grad but no line searching
xs[i+1] = xs[i] - np.dot(alpha,dfdx(xs[i]))
plt.plot(xs[:,0],xs[:,1],'g-o')

##################################################
# Conjugate gradient method
##################################################
# Number of iterations
n = 8
# Use this alpha for the first line search
alpha = 0.15
neg = [[-1.0,0.0],[0.0,-1.0]]
# Initialize xc
xc = np.zeros((n+1,2))
xc[0] = x_start
# Initialize delta_gc
delta_cg = np.zeros((n+1,2))
# Initialize gc
gc = np.zeros((n+1,2))
# Get gradient at start location (df/dx or grad(f))
for i in range(n):
gc[i] = dfdx(xc[i])
# Compute search direction and magnitude (dx)
# with dx = - grad but no line searching
if i==0:
beta = 0
delta_cg[i] = - np.dot(alpha,dfdx(xc[i]))
else:
beta = np.dot(gc[i],gc[i]) / np.dot(gc[i-1],gc[i-1])
delta_cg[i] = alpha * np.dot(neg,dfdx(xc[i])) + beta * delta_cg[i-1]
xc[i+1] = xc[i] + delta_cg[i]
plt.plot(xc[:,0],xc[:,1],'y-o')

##################################################
# Quasi-Newton method
##################################################
# Number of iterations
n = 8
# Use this alpha for every line search
alpha = np.linspace(0.1,1.0,n)
# Initialize delta_xq and gamma
delta_xq = np.zeros((2,1))
gamma = np.zeros((2,1))
part1 = np.zeros((2,2))
part2 = np.zeros((2,2))
part3 = np.zeros((2,2))
part4 = np.zeros((2,2))
part5 = np.zeros((2,2))
part6 = np.zeros((2,1))
part7 = np.zeros((1,1))
part8 = np.zeros((2,2))
part9 = np.zeros((2,2))
# Initialize xq
xq = np.zeros((n+1,2))
xq[0] = x_start
# Initialize gradient storage
g = np.zeros((n+1,2))
g[0] = dfdx(xq[0])
# Initialize hessian storage
h = np.zeros((n+1,2,2))
h[0] = [[1, 0.0],[0.0, 1]]
for i in range(n):
# Compute search direction and magnitude (dx)
# with dx = -alpha * inv(h) * grad
delta_xq = -np.dot(alpha[i],np.linalg.solve(h[i],g[i]))
xq[i+1] = xq[i] + delta_xq

# Get gradient update for next step
g[i+1] = dfdx(xq[i+1])

# Get hessian update for next step
gamma = g[i+1]-g[i]
part1 = np.outer(gamma,gamma)
part2 = np.outer(gamma,delta_xq)
part3 = np.dot(np.linalg.pinv(part2),part1)

part4 = np.outer(delta_xq,delta_xq)
part5 = np.dot(h[i],part4)
part6 = np.dot(part5,h[i])
part7 = np.dot(delta_xq,h[i])
part8 = np.dot(part7,delta_xq)
part9 = np.dot(part6,1/part8)

h[i+1] = h[i] + part3 - part9

plt.plot(xq[:,0],xq[:,1],'r-o')
plt.savefig('contour.png')
plt.show()

[$[Get Code]]

More Advanced Solvers

The above implementations are very simple with 7-30 lines of code each. More advanced methods are implemented with Nonlinear Programming (NLP) and Mixed Integer Nonlinear Programming Solvers (MINLP) solvers such as APOPT (MINLP solver), BPOPT (NLP solver), and IPOPT (NLP solver). The following Python Gekko code demonstrates the performance with these three solvers by changing m.options.SOLVER to 1=APOPT, 2=BPOPT, 3=IPOPT.

from gekko import GEKKO
m = GEKKO()
x1 = m.Var(-3)
x2 = m.Var(2)
m.Minimize(x1**2-2*x1*x2+4*x2**2)
m.options.SOLVER = 2 # 1=APOPT, 2=BPOPT, 3=IPOPT
m.solve()
print(x1.value[0],x2.value[0])

[$[Get Code]]

The simple objective only requires an unconstrained Quadratic Programming (QP) solver with the objective function.

$$\min_{x_1,x_2} \left(x_1^2-2 x_1 x_2 + 4 x_2^2\right)$$

The NLP and MINLP solvers can also solve the problem. APOPT converges in 4 iterations using 1st derivatives, BPOPT converges in 3 iterations with 1st and 2nd derivatives, and IPOPT converges in 2 iterations with 1st and 2nd derivatives.

This assignment can be completed in groups of two. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.

Generative AI Learning

Use these prompts to test your understanding after completing the search direction homework. Direct the AI - it may check your iterations, but do the hand iterations yourself first: the point of this assignment is to feel what each algorithm does.

"Quiz me with 5 questions, one at a time, on search directions for unconstrained optimization: why steepest descent zigzags on an elongated quadratic, what makes Newton's method converge in one step on a quadratic and what it costs (Hessian and its factorization), what the BFGS update builds from gradient differences and why it stays positive definite, how conjugate gradient avoids storing any matrix, and what a line search contributes regardless of the direction chosen. Grade my answers and list my misconceptions."

"I performed hand iterations of {steepest descent / conjugate gradient / BFGS} on f = x1^2 - 2 x1 x2 + 4 x2^2 starting from {your point}. Here are my directions, step lengths, and iterates: {paste}. Do NOT redo the whole calculation. Audit it like a grader: check the first gradient, check that each search direction has the right sign and property (descent? conjugate? uses the updated inverse Hessian?), and find the first iteration where I went wrong, if any. Then ask me to predict how many iterations each method needs to reach the minimum of this quadratic, and grade my prediction."

Discussion Questions

On the quadratic in this page, Newton's method finishes in one step and BFGS in about n steps - so why do practical solvers (including IPOPT) not simply use exact Newton everywhere?
Steepest descent uses only first derivatives, and so does BFGS. Where does BFGS get its curvature information, and what assumption breaks if the objective is noisy?
A colleague reports "the optimizer converged" because the objective changed by less than 1e-8 between iterations. Give two situations where that criterion passes far from any minimum, and a better test (hint: what should the gradient be?).
If the variables of a problem differ by six orders of magnitude, which of the four methods on this page suffers most, and what does rescaling the variables do to the contours?

What to Turn In

Submit a short report (PDF, 1-2 pages) that curates your results into a demonstration of what you learned. You may use Generative AI to help write the report, but the iterations, comparisons, and interpretations must be your own. Answer these questions:

Show your iteration paths for steepest descent, conjugate gradient, and BFGS on the same contour plot of f = x1^2 - 2 x1 x2 + 4 x2^2. Report iterations to convergence for each with the same tolerance.
From the audit prompt: did the AI find an error in your hand iterations? Show the corrected step if so, or the confirmed first two iterations if not.
Why does steepest descent take many more iterations on this problem than conjugate gradient? Connect your answer to the shape of the contours.
From the quiz prompt: one question you missed and the corrected answer.

Design Optimization