Optimize with GPR Uncertainty
Gaussian Process Regression (GPR) is a probabilistic model and non-parametric method that assumes the function is drawn from a Gaussian process. This allows the model to make predictions with well-defined uncertainty, useful for tasks such as uncertainty-aware decision-making. A more complete mathematical description is provided in the Machine Learning for Engineers course on the Gaussian Process Regression learning page.
Optimization Under Uncertainty
The following sections contain the code blocks for Gekko Optimization of a GPR model that minimizes the GPR prediction and uncertainty.
Import Libraries: Import the necessary libraries including NumPy, Matplotlib, Gekko, and Scikit-learn's Gaussian Process Regressor and kernels. Install Gekko if it isn't already installed.
import matplotlib.pyplot as plt
import pandas as pd
import sklearn.gaussian_process as gp
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split
try:
from gekko.ML import Gekko_GPR
from gekko import GEKKO
except:
!pip install gekko
from gekko.ML import Gekko_GPR
from gekko import GEKKO
Generate Data: Define a function to generate data with noise and visualizes this data along with the true function.
return np.cos(2*np.pi*x)
#represent noise from a data sample
N = 150
p1 = np.linspace(0.00,0.3,15)
p2 = np.linspace(0.32,0.4,40)
p3 = np.linspace(0.42,1.2,45)
xl = np.concatenate((p1,p2,p3))
np.random.seed(14)
n1 = np.random.normal(0,0.3,15)
n2 = np.random.normal(0,0.1,40)
n3 = np.random.normal(0,0.3,45)
noise = np.concatenate((n1,n2,n3))
y_measured = f(xl) + noise
plt.figure(figsize=(6,3.5))
plt.plot(xl,f(xl),label='source function')
plt.plot(xl,y_measured,'.',label='measured points')
plt.legend()
plt.show()
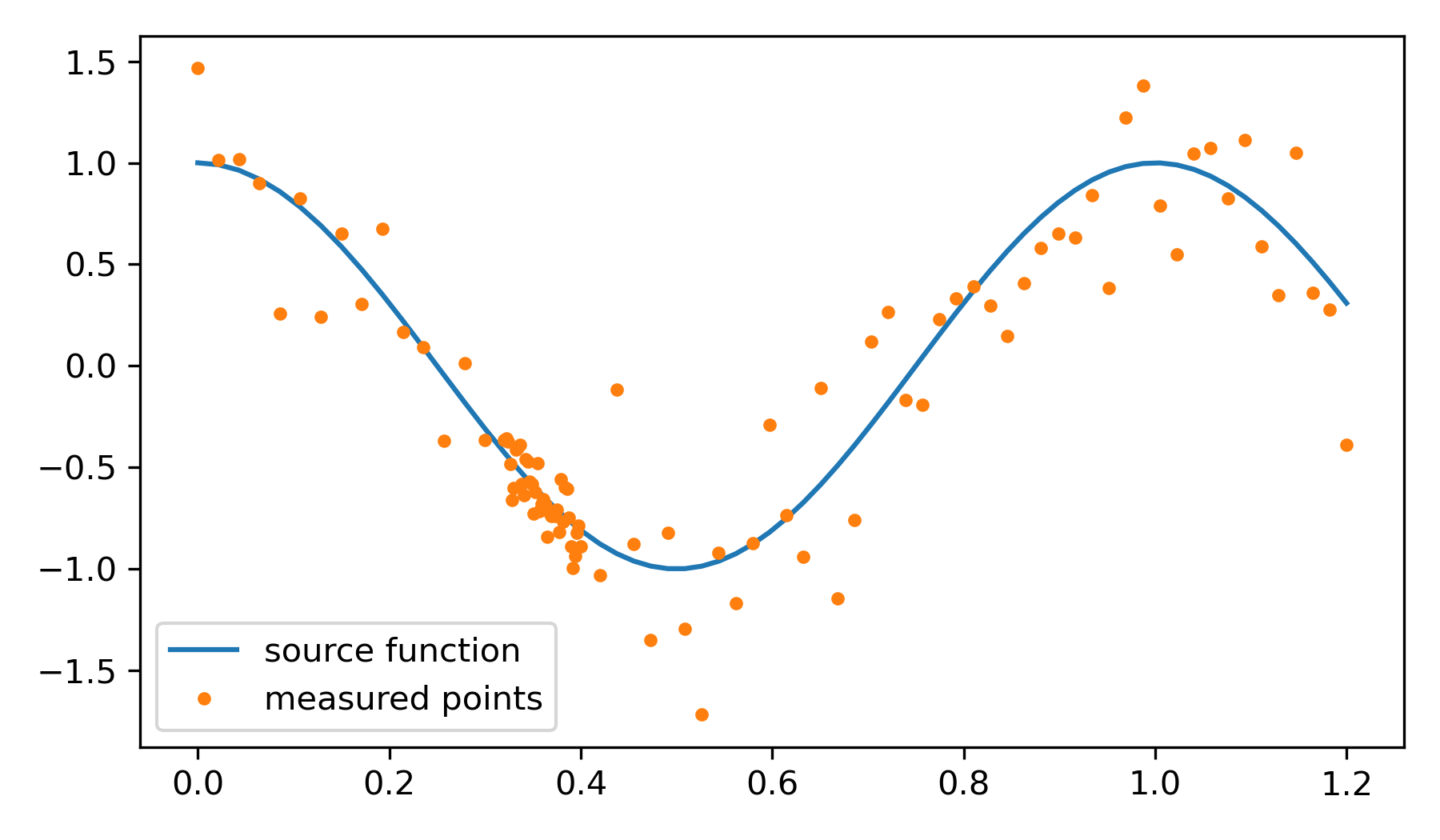
Data Preparation: Data is split into training and testing sets using train_test_split from scikit-learn.
features = ['x']
label = ['y']
train,test = train_test_split(data,test_size=0.2,shuffle=True)
GPR Model Training: A Gaussian Process Regressor (GPR) is created and trained on the training data. The performance of the model is evaluated using the R-squared metric on the test data.
gpr = gp.GaussianProcessRegressor(kernel=k,\
n_restarts_optimizer=10,\
alpha=0.1,\
normalize_y=True)
gpr.fit(train[features],train[label])
r2 = gpr.score(test[features],test[label])
print('gpr r2:',r2)
Model Visualization: The trained GPR model predictions and confidence intervals are plotted against the true function and noisy measurements.
model_pred, model_std = gpr.predict(prediction_data, return_std=True)
t = 1.96 #2 sided 90% Confidence interval z-infinity score
plt.plot(xl,f(xl),label='source function')
plt.plot(xl,y_measured,'.',label='measured points')
plt.plot(xl,model_pred,'--',label='trained model',color='green')
plt.fill_between(xl,model_pred-t*model_std,model_pred+t*model_std,alpha=0.3,color='green')
plt.legend()
plt.show()
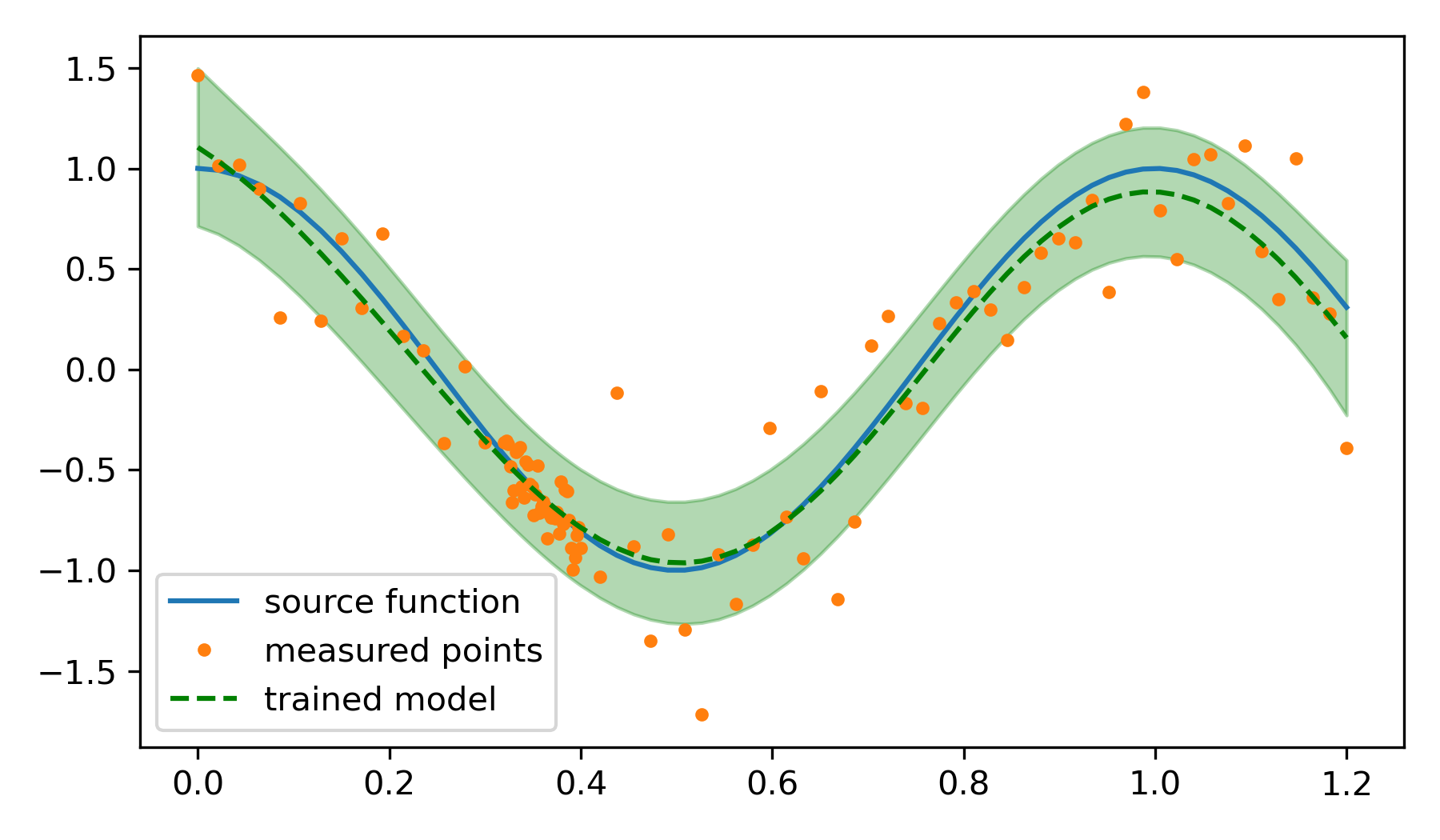
Optimization with Gekko: The Gekko package is used to perform optimization. A variable is created within Gekko and the trained GPR model is used to predict the output and its uncertainty for this variable. Gekko then optimizes this variable to minimize the objective, which in this case is either the predicted value or the uncertainty of the prediction.
x = m.Var(0,lb=0,ub=1)
y,y_std = Gekko_GPR(gpr,m).predict(x,return_std=True)
m.Minimize(y)
m.solve(disp=False)
print('solution:',y.value[0],'std:',y_std.value[0])
print('x:',x.value[0])
print('Gekko Solvetime:',m.options.SOLVETIME,'s')
opt_val = [x.value[0],y.value[0]]
Uncertainty Optimization: uncertainty is minimized.
x = m.Var(0,lb=0,ub=1)
y,y_std = Gekko_GPR(gpr,m).predict(x,return_std=True)
m.Minimize(y_std)
m.solve(disp=False)
print('solution:',y.value[0],'std:',y_std.value[0])
print('x:',x.value[0])
print('Gekko Solvetime:',m.options.SOLVETIME,'s')
opt_val2 = [x.value[0],y.value[0],y_std.value[0]]
Multi-Objective Uncertainty Optimization: uncertainty and expected values are minimized as a weighted sum.
x = m.Var(0,lb=0,ub=1)
y,y_std = Gekko_GPR(gpr,m).predict(x,return_std=True)
m.Minimize(y+50*y_std)
m.solve(disp=False)
print('solution:',y.value[0],'std:',y_std.value[0])
print('x:',x.value[0])
print('Gekko Solvetime:',m.options.SOLVETIME,'s')
opt_val3 = [x.value[0],y.value[0],y_std.value[0]]
Results Visualization: Finally, the optimization results are visualized, showing the points of optimized predicted values and uncertainties.
t = 1.96 #2 sided 90% Confidence interval z-infinity score
plt.figure(figsize=(8,4))
plt.subplot(2,1,1)
plt.plot(xl,f(xl),'b-',label='Source function')
plt.plot(xl,y_measured,'.',label='Measured points')
plt.plot(xl,model_pred,'--',label='GPR model',color='green')
plt.fill_between(xl,model_pred-t*model_std,model_pred+t*model_std,alpha=0.3,color='green')
plt.scatter([opt_val[0]],[opt_val[1]],label='GPR model minimized',color='red',marker='s',s=100,zorder=3)
plt.scatter([opt_val2[0]],[opt_val2[1]],label='GPR uncertainty minimized',color='black',marker='o',s=100,zorder=3)
plt.scatter([opt_val3[0]],[opt_val3[1]],label='Combined optimization',color='blue',marker='^',s=100,zorder=3)
plt.legend(loc='center left',bbox_to_anchor=(1, 0.5),fontsize=10,frameon=False)
plt.subplot(2,1,2)
plt.plot(xl,model_std,'k--',label='GPR uncertainty')
plt.scatter([opt_val2[0]],[opt_val2[2]],label='GPR uncertainty minimized',color='black',marker='o',s=100,zorder=3)
plt.legend(loc='center left',bbox_to_anchor=(1, 0.5),fontsize=10,frameon=False)
plt.tight_layout()
plt.show()
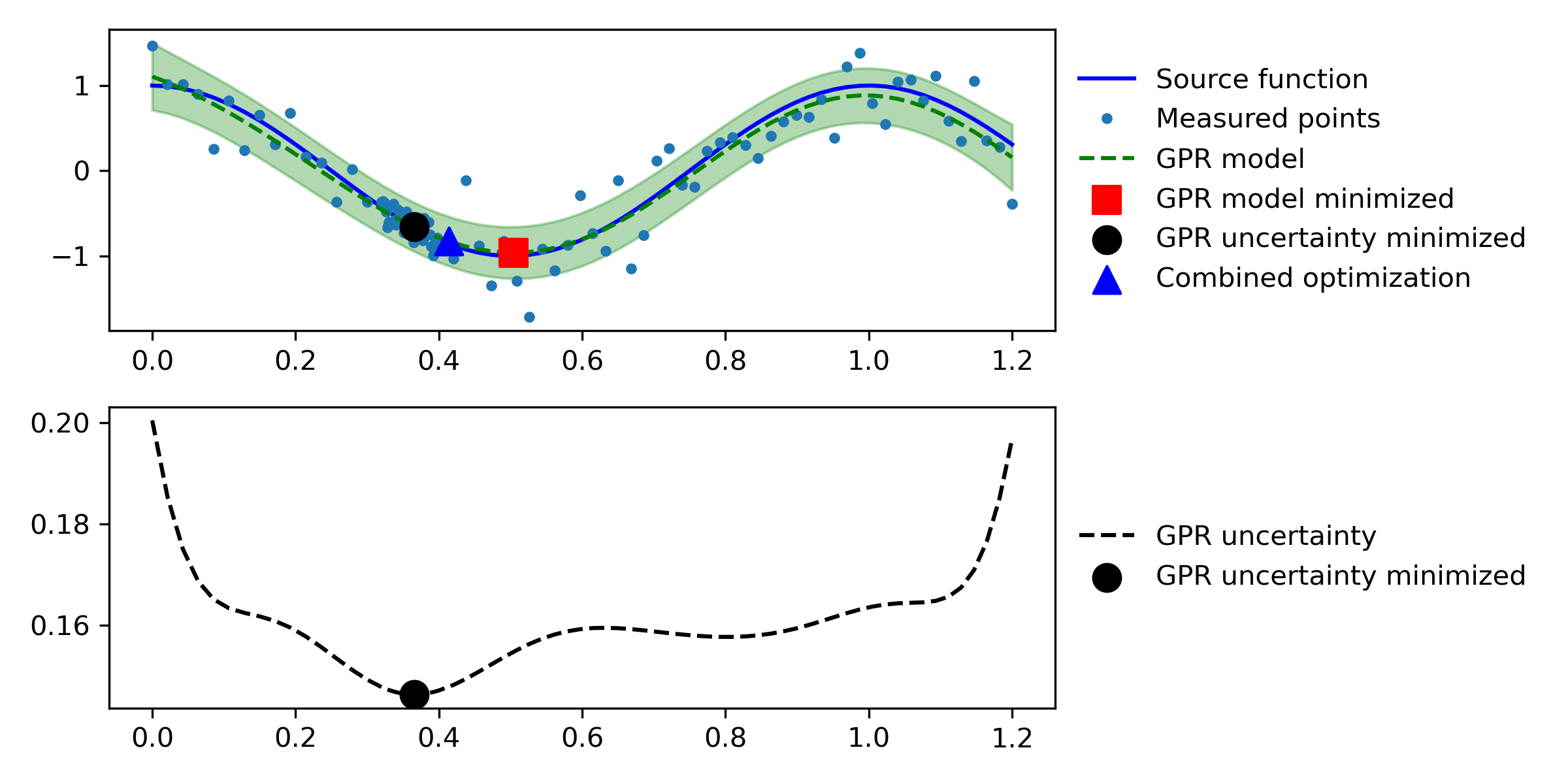
Thanks to LaGrande Gunnell for adding the ML library to Gekko and for the example problem.



