Transfer Functions in Block Diagrams
 |  |  |  |
|---|
One source of transfer functions is from Balance Equations that relate inputs and outputs. Transfer functions are compact representations of dynamic systems and the differential equations become algebraic expressions that can be manipulated or combined with other expressions. The first step in creating a transfer function is to convert each term of a differential equation with a Laplace transform as shown in the table of Laplace transforms. A transfer function, G(s), relates an input, U(s), to an output, Y(s).
$$G(s) = \frac{Y(s)}{U(s)}$$
Do the following, assuming that q and V are constant:
- Transform each equation in to the Laplace domain.
- Find the transfer function between the specified variables.
- Define the time constant and the gain for each transfer function in terms of the parameters given.
The following equations are linearized and variables are in deviation form with `y'(t) = y(t) - y_{0}`.
Exercise 1
Find `{C(s)}/{C_i(s)}`:
$$\frac{dc'(t)}{dt} = \frac{q}{V} c_i'(t) - \frac{q}{V} c'(t) $$
Exercise 2
Find `{C(s)}/{C_i(s)}`:
$$\frac{dc'(t)}{dt} = \frac{q}{V} c_i'(t) - \left(\frac{q}{V} + 2 k_2 \bar c\right) c'(t) $$
Exercise 3
The inlet temperature `T_i(t)` is a process disturbance and the heater `Q(s)` is adjusted to maintain the outlet temperature `T(t)` at a specified set point. Start with the following energy balance and find `{T(s)}/{T_i(s)}` and `{T(s)}/{Q(s)}`.
$$\frac{dT'(t)}{dt} = \frac{q}{V} \left(T_i'(t)-T'(t)\right) + \frac{Q'(t)}{\rho\,V\,C_p} $$
Determine if the two transfer functions are combined in parallel (additive) or series (multiplicative) and input the transfer functions in the appropriate boxes.
Transfer Functions in Parallel
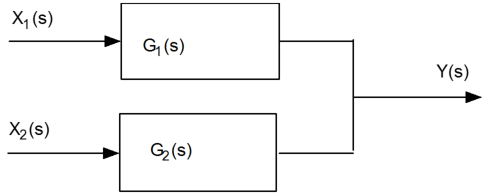
Transfer Functions in Series

Show how the two transfer functions `{T(s)}/{T_i(s)}` and `{T(s)}/{Q(s)}` would fit into an overall control block diagram and label each block and the signal connections between each block. Cross off any blocks not needed for this problem.
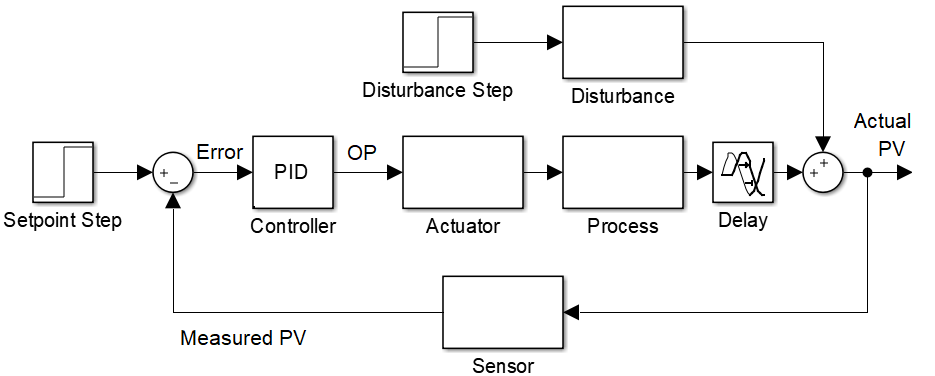
Solution
What to Turn In
- Exercise 1: Laplace transform of the mass balance equation and derivation of the transfer function `(C(s))/(C_i(s))`, including gain and time constant.
- Exercise 2: Laplace transform and derivation of the modified concentration transfer function `(C(s))/(C_i(s))` with reaction term, including expressions for gain and time constant.
- Exercise 3: Laplace transform of the energy balance equation to find `(T(s))/(T_i(s))` and `(T(s))/(Q(s))`. Determine if they are combined in parallel or series and illustrate in a labeled block diagram.