Quiz on Transfer Functions

Information for Questions 1-3: Two reactors are operated in parallel and the output of each is mixed in a blending tank. The inputs (`U_1` and `U_2`) are cooling jacket temperatures. The reactor outputs (`X_1` and `X_2`) are reactor concentrations that are mixed (`X_3`) and blended (`Y`).

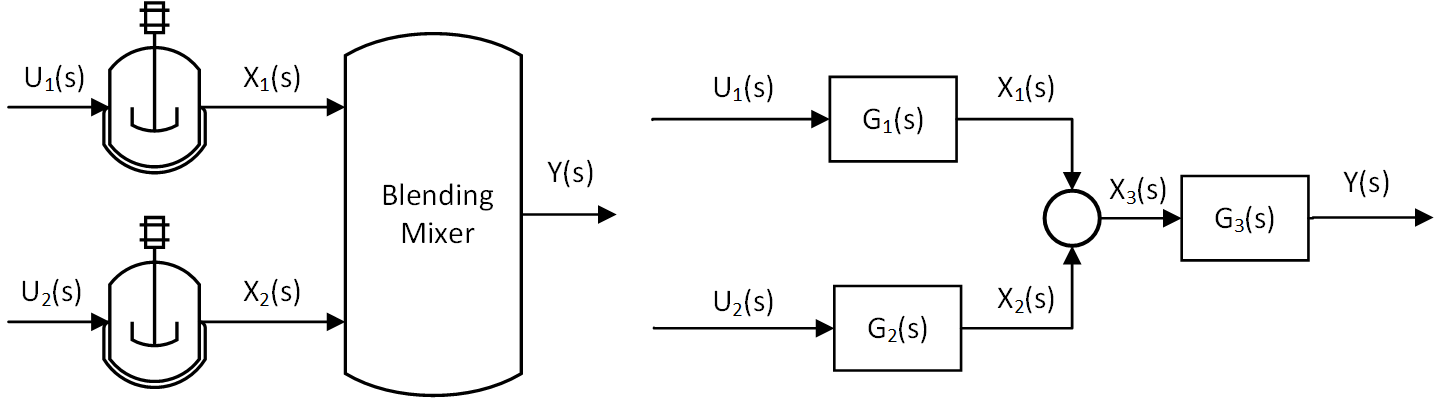
1. What is the expression for reactor outlet `X_2` in terms of input `U_2`?

A. `X_2 = X_1 U_1`
Incorrect. Use the transfer function `G_2` and input `U_2`
B. `X_2 = G_1 U_2`
Incorrect. Use the transfer function `G_2`
C. `X_2 = G_2 U_2`
Correct. The transfer function `G_2` relates the input `U_2` to the output `X_2`
D. `X_2 = G_1 U_1`
Incorrect. Use the transfer function `G_2` and input `U_2`

2. What is the expression for the mixed reactor outlet `X_3` in terms of inputs `U_1` and `U_2`?

A. `X_3 = G_1 G_2 U_1 U_2`
Incorrect. Processes in parallel are additive, not multiplicative
B. `X_3 = X_1 U_1 + X_2 U_2`
Incorrect. Use transfer functions `G_1` and `G_2` instead of `X_1` and `X_2`
C. `X_3 = X_1 + X_2`
Incorrect. This is correct but it is not in terms of the inputs
D. `X_3 = G_1 U_1 + G_2 U_2`
Correct. `X_3 = X_1 + X_2 = G_1 U_1 + G_2 U_2`

3. What is the expression for the blender outlet `Y` in terms of inputs `U_1` and `U_2`?

A. `Y = G_3 X_3`
Incorrect. This is correct but not in terms of `U_1` and `U_2`
B. `Y = G_3 (X_1 + X_2)`
Incorrect. This is correct but not in terms of `U_1` and `U_2`
C. `Y = G_3 G_1 U_1 + G_3 G_2 U_2`
Correct. This is in terms of the inputs `U_1` and `U_2` and the transfer functions
D. `Y = G_3 X_3 G_1 X_1 U_1 + G_3 X_3 G_2 X_2 U_2`
Incorrect. The intermediate signals `X_1`, `X_2`, and `X_3` are not in the input to output expression

4. What are the requirements to obtain a transfer function? Select two correct answers.

A. Nonlinear equations
Incorrect. Only linear equations or linearized nonlinear equations can be transformed to Laplace domain
B. Linear equations
Correct. Only linear equations can be transformed to Laplace domain
C. Differential equation with multiple inputs and one output
Incorrect. A transfer function relates one input to one output
D. Differential equation with one input and one output
Correct. A transfer function relates one input to one output

5. What is the gain of the transfer function `G(s) = {5(s + 1)}/{(s + 3)^2}`?

A. 5/3
Incorrect. `K_p = \lim_{s \to 0} {5(s + 1)}/{(s + 3)^2}`
B. 5/9
Correct. `K_p = \lim_{s \to 0} {5(s + 1)}/{(s + 3)^2} = {5(1)}/{3^2} = 5/9`
C. 0
Incorrect. `K_p = \lim_{s \to 0} {5(s + 1)}/{(s + 3)^2}`
D. 1
Incorrect. `K_p = \lim_{s \to 0} {5(s + 1)}/{(s + 3)^2}`
💬