Time Delay in Dynamic Systems
 |  |  |  |  |  |
|---|
Time delay is a shift in the effect of an input on an output dynamic response. A first-order linear system with time delay is:
$$\tau_p \frac{dy(t)}{dt} = -y(t) + K_p u\left(t-\theta_p\right)$$
has variables y(t) and u(t) and three unknown parameters with
$$K_p \quad \mathrm{= Process \; gain}$$
$$\tau_p \quad \mathrm{= Process \; time \; constant}$$
$$\theta_p \quad \mathrm{= Process \; dead \; time}$$
The time delay `\theta_p` is expressed as a time shift in the input variable u(t).
$$u\left(t-\theta_p\right)$$
$$y(t \lt \theta_p) = y(0)$$
$$y(t \ge \theta_p) = \left( e^{-\left(t - \theta_p \right) / \tau_p}\right) y(0) + \left( 1 - e^{-\left(t - \theta_p \right) / \tau_p} \right) K_p \Delta u $$
For a step change `\Delta u`, the analytical solution for a first-order linear system without time delay (x(t) = y(t) with `theta_p=0`)
$$\tau_p \frac{dx(t)}{dt} = -y(t) + K_p u\left(t\right)$$
is
$$x(t) = K_p \left(1-\exp\left(\frac{-t}{\tau_p}\right)\right) \Delta u$$
With dead-time, the solution becomes:
$$y(t) = x \left( t-\theta_p \right) S \left( t-\theta_p \right)$$
$$\quad = K_p \left( 1- \exp\left(-\frac{ t-\theta_p } { \tau_p } \right) \right) \, \Delta u \, S \left( t-\theta_p \right) $$
where
$$S\left(t-\theta_p\right)$$
is a step function that changes from zero to one at `t=theta_p`.
Analytic Solution Derivation with Laplace Transforms
Start with the linear differential equation with time delay:
$$\tau_p \frac{dy(t)}{dt} = -y(t) + K_p u\left(t-\theta_p\right)$$
Perform a Laplace transform from the tables on each part of the equation:
$$\mathcal{L}\left(\tau_p \frac{dy(t)}{dt}\right) = \tau_p \left(s Y(s) - y(0)\right)$$
$$\mathcal{L}\left(-y(t)\right) = -Y(s)$$
$$\mathcal{L}\left(K_p u\left(t-\theta_p\right)\right) = K_p U(s) e^{-\theta_p s}$$
If the input `U(s)` is a step function of size `\Delta u` then:
$$U(s) = \frac{\Delta u}{s}$$
Combining all of the individual Laplace transforms, the equation in Laplace domain with zero initial condition y(0)=0 is then:
$$\tau_p \, s \, Y(s) = -Y(s) + K_p \frac{\Delta u}{s} e^{-\theta_p s}$$
At this point, the equation is algebraic and can be solved for Y(s) by combining terms on each side:
$$\tau_p \, s \, Y(s) + Y(s) = K_p \frac{\Delta u}{s} e^{-\theta_p s}$$
and factoring out the Y(s) term:
$$Y(s) \left(\tau_p \, s + 1\right) = K_p \frac{\Delta u}{s} e^{-\theta_p s}$$
A final steps are to isolate Y(s) on the left side of the equation and perform an inverse Laplace transform to return to the time domain:
$$Y(s) = K_p \frac{\Delta u}{s\,\left(\tau_p \, s + 1\right)} e^{-\theta_p s}$$
$$\mathcal{L}^{-1}\left(Y(s)\right) = y(t) = K_p \left( 1-\exp \left( -\frac{ \left( t-\theta_p \right) } { \tau_p } \right) \right) \, \Delta u \, S \left( t-\theta_p \right)$$
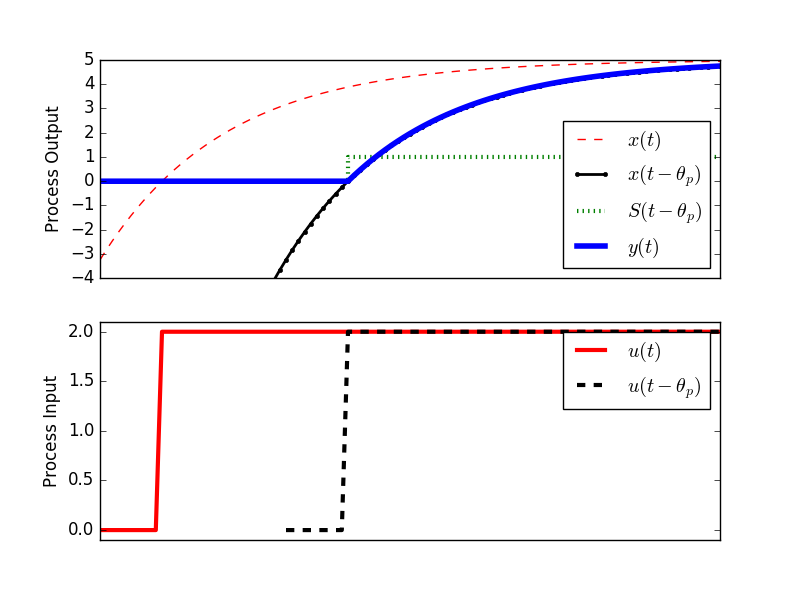
import matplotlib.pyplot as plt
from scipy.integrate import odeint
# specify number of steps
ns = 100
# define time points
t = np.linspace(0,ns/10.0,ns+1)
class model(object):
# process model
Kp = 2.0
taup = 200.0
thetap = 0.0
def process(y,t,u,Kp,taup):
# Kp = process gain
# taup = process time constant
dydt = -y/taup + Kp/taup * u
return dydt
def calc_response(t,m):
# t = time points
# m = process model
Kp = m.Kp
taup = m.taup
thetap = m.thetap
# specify number of steps
ns = len(t)-1
delta_t = t[1]-t[0]
# storage for recording values
op = np.zeros(ns+1) # controller output
pv = np.zeros(ns+1) # process variable
# step input
op[10:]=2.0
# Simulate time delay
ndelay = int(np.ceil(thetap / delta_t))
# loop through time steps
for i in range(0,ns):
# implement time delay
iop = max(0,i-ndelay)
y = odeint(process,pv[i],[0,delta_t],args=(op[iop],Kp,taup))
pv[i+1] = y[-1]
return (pv,op)
# calculate step response
model.Kp = 2.5
model.taup = 2.0
model.thetap = 3.0
(pv,op) = calc_response(t,model)
pv2 = np.zeros(len(t))
for i in range(len(t)):
pv2[i] = model.Kp * (1.0 - np.exp(-(t[i]-model.thetap-1.0)/model.taup))*2.0
pv3 = np.zeros(len(t))
for i in range(len(t)):
pv3[i] = model.Kp * (1.0 - np.exp(-(t[i]-1.0)/model.taup))*2.0
plt.figure(1)
plt.subplot(2,1,1)
frame1 = plt.gca()
frame1.axes.get_xaxis().set_visible(False)
plt.plot(t,pv3,'r--',linewidth=1,label=r'$y(t)$')
plt.plot(t,pv2,'k.-',linewidth=2,label=r'$y(t-\theta_p)$')
plt.plot([0,4,4.0001,10],[0,0,1,1],'g:',linewidth=3,label=r'$S(t- \theta _p)$')
plt.plot(t,pv,'b-',linewidth=4,label=r'$x(t)$')
plt.legend(loc='best')
plt.ylabel('Process Output')
plt.ylim([-4,5])
plt.subplot(2,1,2)
frame1 = plt.gca()
frame1.axes.get_xaxis().set_visible(False)
plt.plot(t,op,'r-',linewidth=3,label=r'$u(t)$')
plt.plot(t+3.0,op,'k--',linewidth=3,label=r'$u(t-\theta_p)$')
plt.ylim([-0.1,2.1])
plt.xlim([0,10])
plt.legend(loc='best')
plt.ylabel('Process Input')
plt.xlabel('Time')
plt.savefig('output.png')
plt.show()
