Dynamics and Control

Differential equations are solved in Python with the Scipy.integrate package using function odeint or solve_ivp.

Jupyter Notebook ODEINT Examples on GitHub

Jupyter Notebook ODEINT Examples in Google Colab

ODEINT requires three inputs:

 y = odeint(model, y0, t)

1. model: Function name that returns derivative values at requested y and t values as dydt = model(y,t)
2. y0: Initial conditions of the differential states
3. t: Time points at which the solution should be reported. Additional internal points are often calculated to maintain accuracy of the solution but are not reported.

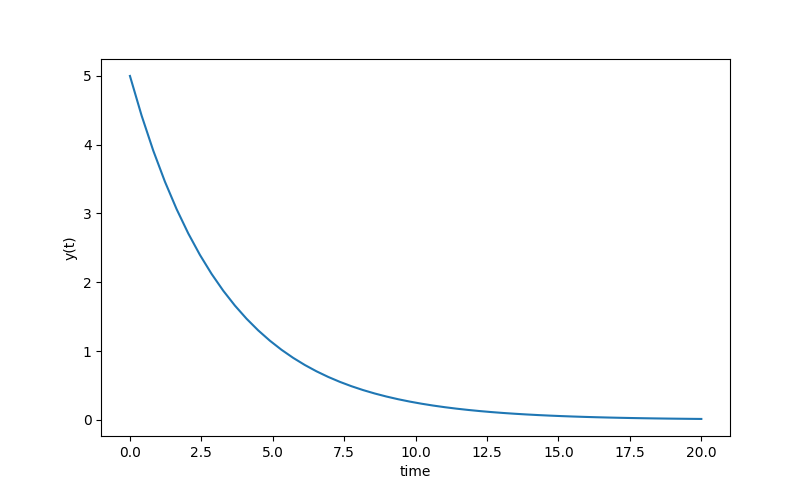
An example of using ODEINT is with the following differential equation with parameter k=0.3, the initial condition y₀=5 and the following differential equation.

$$\frac{dy(t)}{dt} = -k \; y(t)$$

The Python code first imports the needed Numpy, Scipy, and Matplotlib packages. The model, initial conditions, and time points are defined as inputs to ODEINT to numerically calculate y(t).

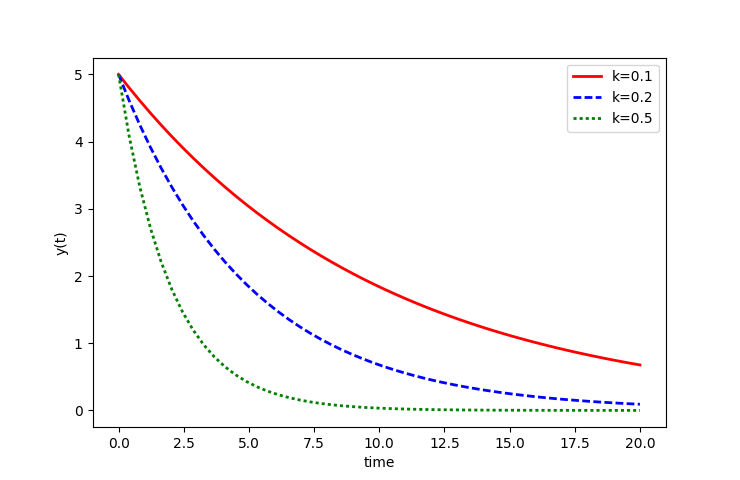
An optional fourth input is args that allows additional information to be passed into the model function. The args input is a tuple sequence of values. The argument k is now an input to the model function by including an addition argument.

Exercises

Find a numerical solution to the following differential equations with the associated initial conditions. Expand the requested time horizon until the solution reaches a steady state. Show a plot of the states (x(t) and/or y(t)). Report the final value of each state as `t \to \infty`.

Problem 1

$$\frac{dy(t)}{dt} = -y(t) + 1$$

$$y(0) = 0$$

import numpy as np
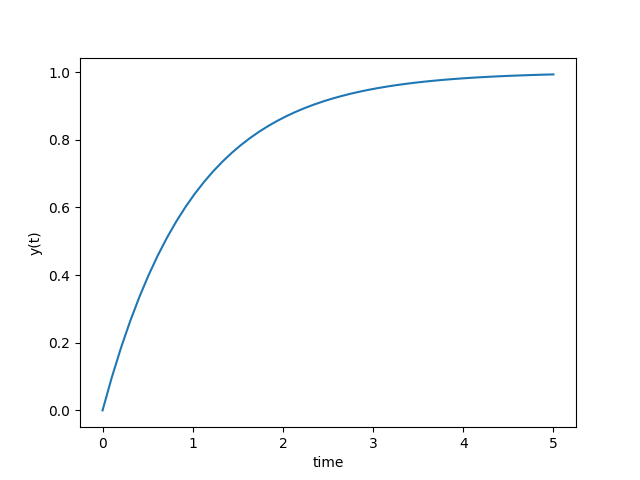
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# function that returns dy/dt
def model(y,t):
    dydt = -y + 1.0
    return dydt

# initial condition
y0 = 0

# time points
t = np.linspace(0,5)

# solve ODE
y = odeint(model,y0,t)

# plot results
plt.plot(t,y)
plt.xlabel('time')
plt.ylabel('y(t)')
plt.show()

[$[Get Code]]

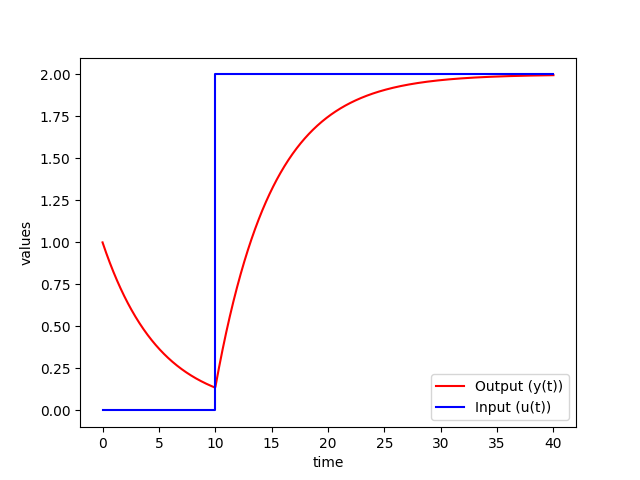
Problem 2

$$5 \; \frac{dy(t)}{dt} = -y(t) + u(t)$$

$$y(0) = 1$$

`u` steps from 0 to 2 at `t=10`

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# function that returns dy/dt
def model(y,t):
    # u steps from 0 to 2 at t=10
    if t<10.0:
        u = 0
    else:
        u = 2
    dydt = (-y + u)/5.0
    return dydt

# initial condition
y0 = 1

# time points
t = np.linspace(0,40,1000)

# solve ODE
y = odeint(model,y0,t)

# plot results
plt.plot(t,y,'r-',label='Output (y(t))')
plt.plot([0,10,10,40],[0,0,2,2],'b-',label='Input (u(t))')
plt.ylabel('values')
plt.xlabel('time')
plt.legend(loc='best')
plt.show()

[$[Get Code]]

Problem 3

Solve for `x(t)` and `y(t)` and show that the solutions are equivalent.

$$\frac{dx(t)}{dt} = 3 \; exp(-t)$$ $$\frac{dy(t)}{dt} = 3 - y(t)$$ $$x(0) = 0$$ $$y(0) = 0$$

import numpy as np
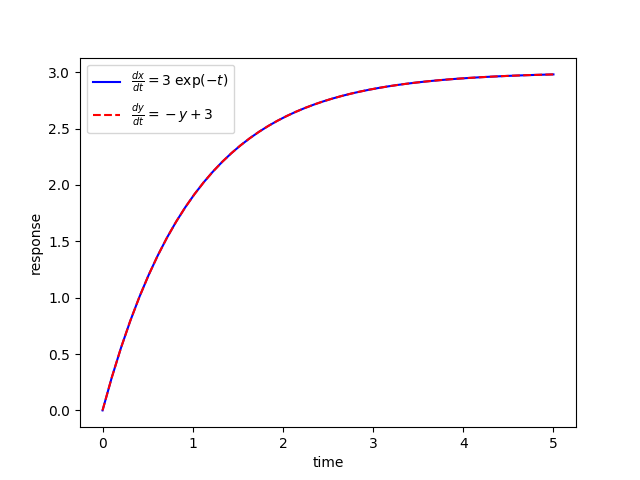
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# function that returns dz/dt
def model(z,t):
    dxdt = 3.0 * np.exp(-t)
    dydt = -z[1] + 3
    dzdt = [dxdt,dydt]
    return dzdt

# initial condition
z0 = [0,0]

# time points
t = np.linspace(0,5)

# solve ODE
z = odeint(model,z0,t)

# plot results
plt.plot(t,z[:,0],'b-',label=r'$\frac{dx}{dt}=3 \; \exp(-t)$')
plt.plot(t,z[:,1],'r--',label=r'$\frac{dy}{dt}=-y+3$')
plt.ylabel('response')
plt.xlabel('time')
plt.legend(loc='best')
plt.show()

[$[Get Code]]

Problem 4

$$2 \; \frac{dx(t)}{dt} = -x(t) + u(t)$$

$$5 \; \frac{dy(t)}{dt} = -y(t) + x(t)$$

$$u = 2 \, S(t-5), \; x(0) = 0, \; y(0) = 0$$

where `S(t-5)` is a step function that changes from zero to one at `t=5`. When it is multiplied by two, it changes from zero to two at that same time, `t=5`.

import numpy as np
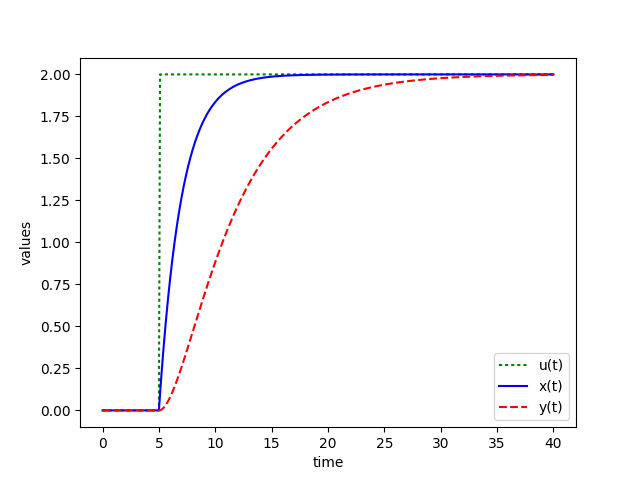
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# function that returns dz/dt
def model(z,t,u):
    x = z[0]
    y = z[1]
    dxdt = (-x + u)/2.0
    dydt = (-y + x)/5.0
    dzdt = [dxdt,dydt]
    return dzdt

# initial condition
z0 = [0,0]

# number of time points
n = 401

# time points
t = np.linspace(0,40,n)

# step input
u = np.zeros(n)
# change to 2.0 at time = 5.0
u[50:] = 2.0

# store solution
x = np.empty_like(t)
y = np.empty_like(t)
# record initial conditions
x[0] = z0[0]
y[0] = z0[1]

# solve ODE
for i in range(1,n):
    # span for next time step
    tspan = [t[i-1],t[i]]
    # solve for next step
    z = odeint(model,z0,tspan,args=(u[i],))
    # store solution for plotting
    x[i] = z[1][0]
    y[i] = z[1][1]
    # next initial condition
    z0 = z[1]

# plot results
plt.plot(t,u,'g:',label='u(t)')
plt.plot(t,x,'b-',label='x(t)')
plt.plot(t,y,'r--',label='y(t)')
plt.ylabel('values')
plt.xlabel('time')
plt.legend(loc='best')
plt.show()

[$[Get Code]]

Another Python package that solves differential equations is GEKKO. See this link for the same tutorial in GEKKO versus ODEINT.