Dynamics and Control

A second-order linear system with time delay is an empirical description of potentially oscillating dynamic processes. These systems are common in chemical processes, mechanical systems, and other applications where the output response can exhibit overshoot and oscillations before reaching a steady state.

The general form of the SOPDT model is given by:

$$\tau_s^2 \frac{d^2y}{dt^2} + 2 \zeta \tau_s \frac{dy}{dt} + y = K_p \, u\left(t-\theta_p \right)$$

where:

• `y(t)` is the output variable (e.g., temperature, concentration, position).
• `u(t)` is the input variable (e.g., heater power, feed rate, force).
• `K_p` is the process gain, representing the steady-state change in output per unit change in input.
• `\tau_s` is the second-order time constant, representing the speed of response.
• `\zeta` is the damping factor, determining the degree of oscillation in the response.
• `\theta_p` is the time delay (dead time), representing a delay between the input change and the output response.

Understanding SOPDT Parameters

Each parameter in the SOPDT model significantly influences the system's dynamic behavior:

• Process Gain (`K_p`): Indicates how much the output will eventually change for a unit change in input. A higher gain results in a larger steady-state output.
• Second-Order Time Constant (`\tau_s`): Determines the speed of the system's response. A smaller time constant means a faster response to input changes.
• Damping Factor (`\zeta`):
  • Overdamped (`\zeta > 1`): The system returns to steady state without oscillations but slower.
  • Critically Damped (`\zeta = 1`): Fastest return to steady state without oscillations.
  • Underdamped (`0 < \zeta < 1`): The system oscillates before settling at the steady state.
• Time Delay (`\theta_p`): Represents the delay between an input change and the system's initial response. Common in processes with transport or communication delays.

Simulated Data from the SOPDT Model

To demonstrate how to fit an SOPDT model to data, generate simulated data using a higher-order process model. The simulated data mimics real process behavior, including the dynamic response to changes in the input variable.

Download data_sopdt.txt

# Generate process data as data_sopdt.txt
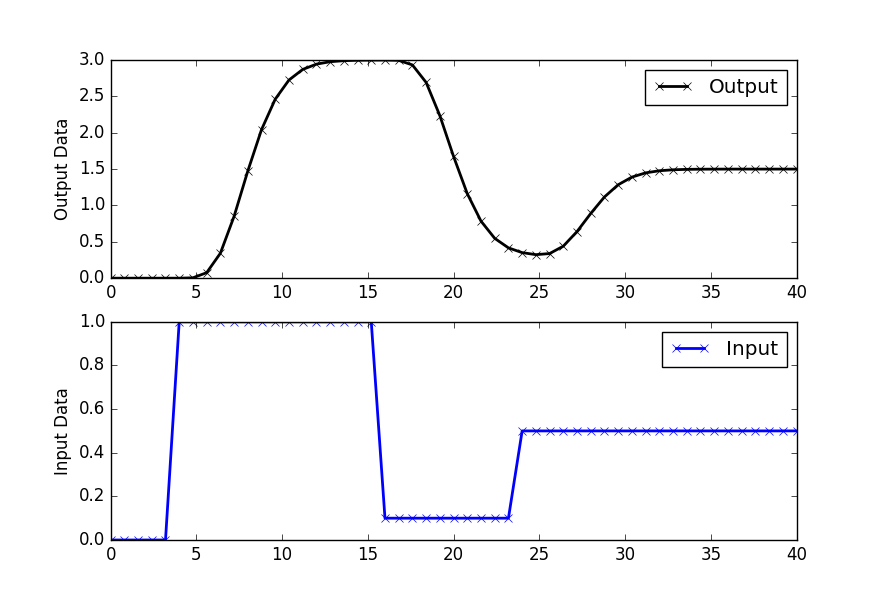
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# Define a higher-order process model to generate data
def process(y, t, n, u, Kp, taup):
    """
    Higher-order process model (nth-order system)
    """
    dydt = np.zeros(n)
    # First derivative
    dydt[0] = (-y[0] + Kp * u) / (taup / n)
    # Higher-order derivatives
    for i in range(1, n):
        dydt[i] = (-y[i] + y[i - 1]) / (taup / n)
    return dydt

# Time points
ns = 100  # Number of time steps
t = np.linspace(0, 40, ns)
delta_t = t[1] - t[0]

# Input vector (piecewise constant input)
u = np.zeros(ns)
u[5:20] = 1.0
u[20:30] = 0.1
u[30:] = 0.5

def sim_process_data():
    """
    Simulate the process data using the higher-order process model.
    """
    n = 10       # Order of the system
    Kp = 2.5     # Process gain
    taup = 5.0   # Process time constant
    yp = np.zeros(ns)  # Initialize output array
    y0 = np.zeros(n)   # Initial conditions
    for i in range(ns - 1):
        ts = [t[i], t[i + 1]]
        args = (n, u[i], Kp, taup)
        y = odeint(process, y0, ts, args=args)
        y0 = y[-1]
        yp[i + 1] = y[-1][n - 1]
    return yp

yp = sim_process_data()

# Save data to a file
data = np.vstack((t, u, yp)).T
np.savetxt('data_sopdt.txt', data, delimiter=',', comments='', header='time,u,y')

# Plot the simulated data
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.plot(t, yp, 'k-', linewidth=2, label='Output y(t)')
plt.ylabel('Output')
plt.legend(loc='best')
plt.subplot(2, 1, 2)
plt.plot(t, u, 'b-', linewidth=2, label='Input u(t)')
plt.ylabel('Input')
plt.xlabel('Time')
plt.legend(loc='best')
plt.tight_layout()
plt.show()

[$[Get Code]]

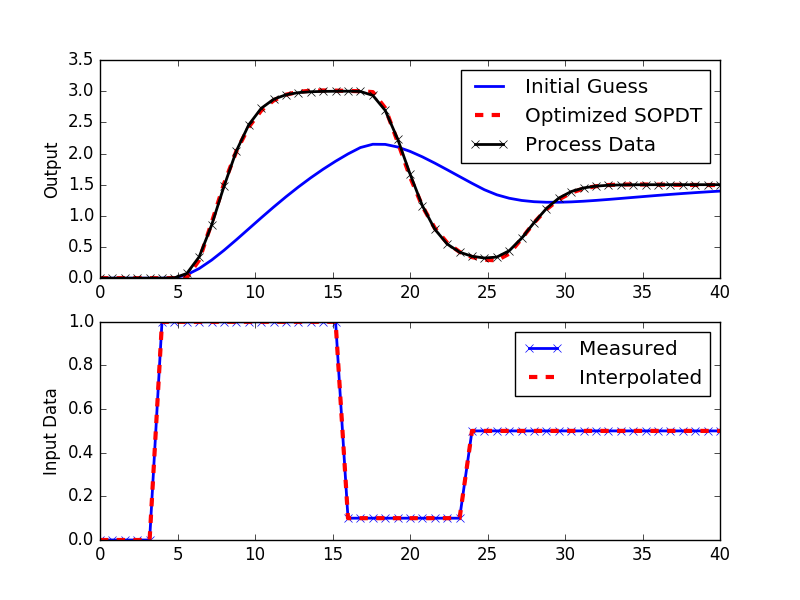
SOPDT Fit to Data

Estimate the SOPDT model parameters (`K_p`, `\tau_s`, `\zeta`, `\theta_p`) that best fit the process data. We use optimization techniques to minimize the sum of squared errors (SSE) between the model predictions and the observed data.

Below are two methods to perform the parameter estimation:

1. Scipy Optimization Tools
2. GEKKO Optimization Suite

Method 1: SOPDT Fit Using Scipy

Method 2: SOPDT Fit Using GEKKO

GEKKO is an optimization suite that facilitates model building and solving differential equations.

Fit SOPDT Model to Experimental Data

In this example, we fit an SOPDT model to real experimental data from a temperature control lab (TCLab). The TCLab is a device with a heater and a temperature sensor, exhibiting second-order dynamics due to thermal mass and heat transfer effects.

Generating Experimental Data

Run the TCLab by applying step changes in the temperature set point and record the heater, temperature, and set point over time.

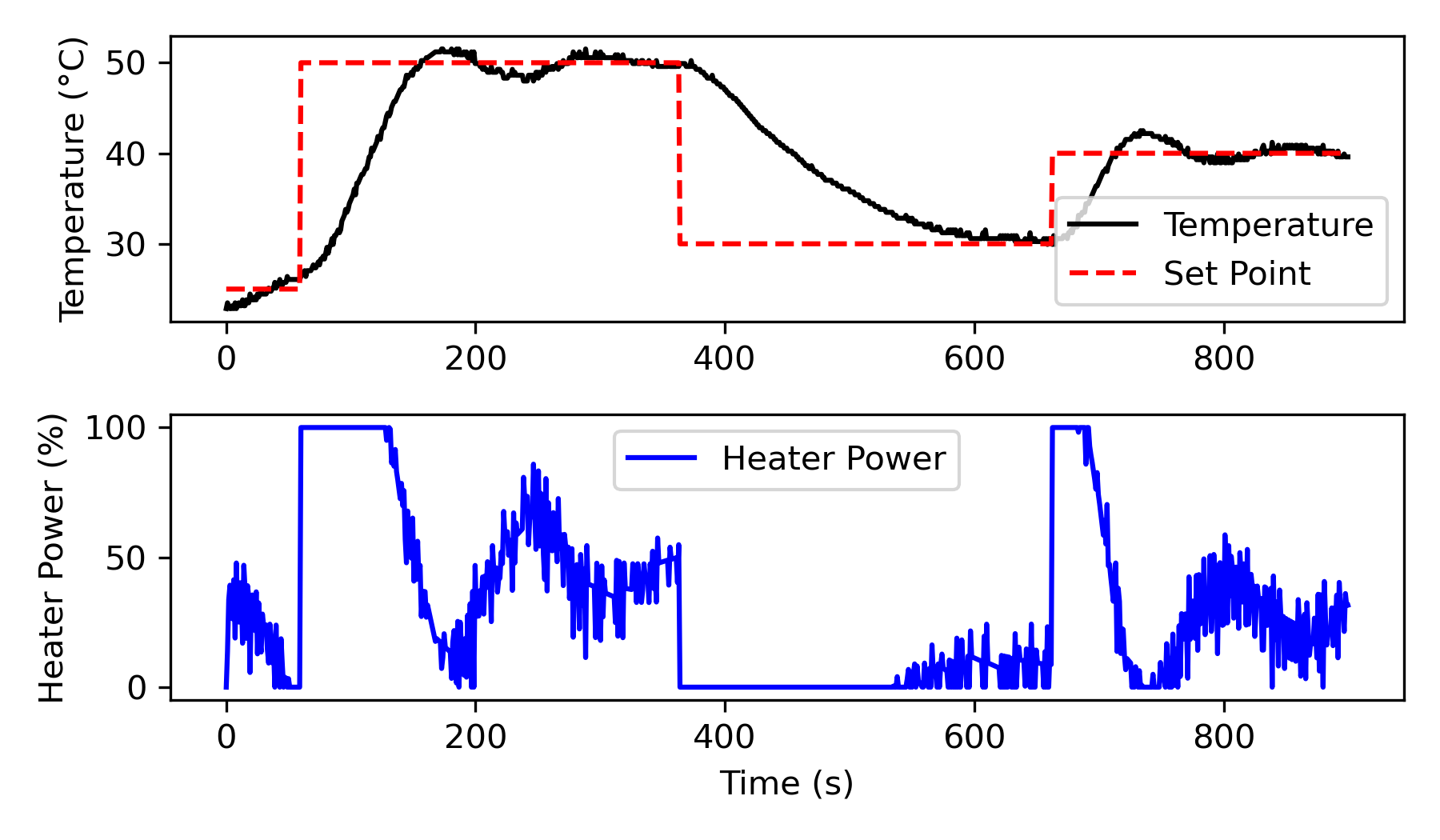
Note: Optionally replace 'tclab_pid.csv' URL with your experimental data file generate from the script above.

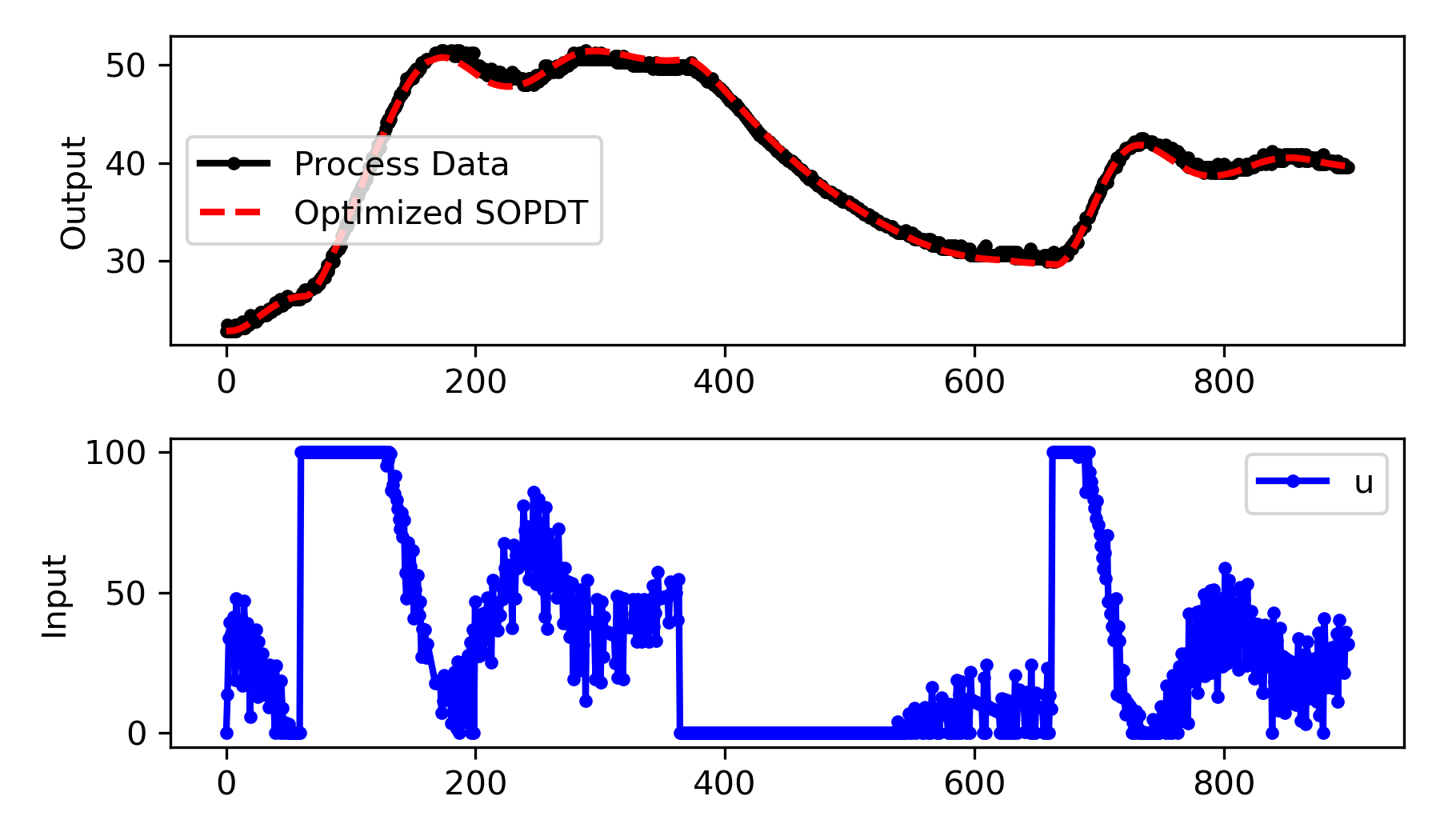
Fit the SOPDT Model to Experimental Data

We use the same fitting approach as before but apply it to the experimental data.

Discussion of Results

The SOPDT model parameters provide insights into the system dynamics.

• Process Gain (`K_p`=0.64): Indicates how much the temperature changes per unit change in heater power.
• Time Constant (`\tau_s`=45.7 sec): Reflects the speed of the temperature response.
• Damping Factor (`\zeta`=1.83): Determines whether the temperature overshoots the setpoint.
• Time Delay (`\theta_p`=4.5 sec): Accounts for the delay between heater activation and temperature change.

Is the damping factor for the heater / temperature response overdamped, critically damped, or underdamped?

• Overdamped `(\zeta>1)`
• Critically damped `(\zeta=1)`
• Underdamped `(0 \le \zeta < 1)`

Comparing the model output with the experimental data helps validate the model accuracy and identify any discrepancies.

Conclusion

Fitting an SOPDT model to process data captures the essential dynamics of a system with potential oscillatory behavior and time delays. The estimated model can be used for controller design, simulation studies, and understanding system behavior.

See Second Order Estimation: Optimization