Quiz on Second Order Regression
 |  |  |  |
|---|
1. What are the limitations of the optimization method to determine parameters for a second order system?
A. Requires a pre-determined underdamped or overdamped system
- Incorrect. The graphical fitting method is different for underdamped or overdamped second order systems. The optimization method is generalized to allow any model form that can be compared to measured values.
B. Requires sufficiently good initial guess values
- Correct. Optimization methods may fail if the initial parameter guess is poor
C. Applicable only for data generated from a step input
- Incorrect. Unlike the graphical method, any input is permitted with optimization
D. Single, small data sets
- Incorrect. The optimization approach is applicable to big data sets from multiple time periods
2. The sim_model function from the example code returns the predictions of the second order model.
# simulate model with x=[Km,taum,thetam]
def sim_model(x):
# input arguments
Kp = x[0]
taus = x[1]
zeta = x[2]
thetap = x[3]
# storage for model values
xm = np.zeros((ns,2)) # model
# initial condition
xm[0] = xp0
# loop through time steps
for i in range(0,ns-1):
ts = [t[i],t[i+1]]
inputs = (uf,Kp,taus,zeta,thetap)
# turn off warnings
with warnings.catch_warnings():
warnings.simplefilter("ignore")
# integrate SOPDT model
x = odeint(sopdt,xm[i],ts,args=inputs)
xm[i+1] = x[-1]
y = xm[:,0]
return y
def sim_model(x):
# input arguments
Kp = x[0]
taus = x[1]
zeta = x[2]
thetap = x[3]
# storage for model values
xm = np.zeros((ns,2)) # model
# initial condition
xm[0] = xp0
# loop through time steps
for i in range(0,ns-1):
ts = [t[i],t[i+1]]
inputs = (uf,Kp,taus,zeta,thetap)
# turn off warnings
with warnings.catch_warnings():
warnings.simplefilter("ignore")
# integrate SOPDT model
x = odeint(sopdt,xm[i],ts,args=inputs)
xm[i+1] = x[-1]
y = xm[:,0]
return y
What is the purpose of the objective function?
# define objective
def objective(x):
# simulate model
ym = sim_model(x)
# calculate objective
obj = 0.0
for i in range(len(ym)):
obj = obj + (ym[i]-yp[i])**2
# return result
return obj
def objective(x):
# simulate model
ym = sim_model(x)
# calculate objective
obj = 0.0
for i in range(len(ym)):
obj = obj + (ym[i]-yp[i])**2
# return result
return obj
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from scipy.optimize import minimize
from scipy.interpolate import interp1d
import warnings
# Import data file
# Column 1 = time (t)
# Column 2 = input (u)
# Column 3 = output (yp)
data = np.loadtxt('data.txt',delimiter=',')
u0 = data[0,1]
y0 = data[0,2]
xp0 = [y0,0.0]
t = data[:,0].T - data[0,0]
u = data[:,1].T
yp = data[:,2].T
# specify number of steps
ns = len(t)
delta_t = t[1]-t[0]
# create linear interpolation of the u data versus time
uf = interp1d(t,u)
def sopdt(x,t,uf,Kp,taus,zeta,thetap):
# Kp = process gain
# taus = second order time constant
# zeta = damping factor
# thetap = model time delay
# ts^2 dy2/dt2 + 2 zeta taus dydt + y = Kp u(t-thetap)
# time-shift u
try:
if (t-thetap) <= 0:
um = uf(0.0)
else:
um = uf(t-thetap)
except:
# catch any error
um = u0
# two states (y and y')
y = x[0] - y0
dydt = x[1]
dy2dt2 = (-2.0*zeta*taus*dydt - y + Kp*(um-u0))/taus**2
return [dydt,dy2dt2]
# simulate model with x=[Km,taum,thetam]
def sim_model(x):
# input arguments
Kp = x[0]
taus = x[1]
zeta = x[2]
thetap = x[3]
# storage for model values
xm = np.zeros((ns,2)) # model
# initial condition
xm[0] = xp0
# loop through time steps
for i in range(0,ns-1):
ts = [t[i],t[i+1]]
inputs = (uf,Kp,taus,zeta,thetap)
# turn off warnings
with warnings.catch_warnings():
warnings.simplefilter("ignore")
# integrate SOPDT model
x = odeint(sopdt,xm[i],ts,args=inputs)
xm[i+1] = x[-1]
y = xm[:,0]
return y
# define objective
def objective(x):
# simulate model
ym = sim_model(x)
# calculate objective
obj = 0.0
for i in range(len(ym)):
obj = obj + (ym[i]-yp[i])**2
# return result
return obj
# initial guesses
p0 = np.zeros(4)
p0[0] = 3 # Kp
p0[1] = 5.0 # taup
p0[2] = 1.0 # zeta
p0[3] = 2.0 # thetap
# show initial objective
print('Initial SSE Objective: ' + str(objective(p0)))
# optimize Kp, taus, zeta, thetap
solution = minimize(objective,p0)
# with bounds on variables
#no_bnd = (-1.0e10, 1.0e10)
#low_bnd = (0.01, 1.0e10)
#bnds = (no_bnd, low_bnd, low_bnd, low_bnd)
#solution = minimize(objective,p0,method='SLSQP',bounds=bnds)
p = solution.x
# show final objective
print('Final SSE Objective: ' + str(objective(p)))
print('Kp: ' + str(p[0]))
print('taup: ' + str(p[1]))
print('zeta: ' + str(p[2]))
print('thetap: ' + str(p[3]))
# calculate model with updated parameters
ym1 = sim_model(p0)
ym2 = sim_model(p)
# plot results
plt.figure()
plt.subplot(2,1,1)
plt.plot(t,ym1,'b-',linewidth=2,label='Initial Guess')
plt.plot(t,ym2,'r--',linewidth=3,label='Optimized SOPDT')
plt.plot(t,yp,'k--',linewidth=2,label='Process Data')
plt.ylabel('Output')
plt.legend(loc='best')
plt.subplot(2,1,2)
plt.plot(t,u,'bx-',linewidth=2)
plt.plot(t,uf(t),'r--',linewidth=3)
plt.legend(['Measured','Interpolated'],loc='best')
plt.ylabel('Input Data')
plt.savefig('results.png')
plt.show()
import matplotlib.pyplot as plt
from scipy.integrate import odeint
from scipy.optimize import minimize
from scipy.interpolate import interp1d
import warnings
# Import data file
# Column 1 = time (t)
# Column 2 = input (u)
# Column 3 = output (yp)
data = np.loadtxt('data.txt',delimiter=',')
u0 = data[0,1]
y0 = data[0,2]
xp0 = [y0,0.0]
t = data[:,0].T - data[0,0]
u = data[:,1].T
yp = data[:,2].T
# specify number of steps
ns = len(t)
delta_t = t[1]-t[0]
# create linear interpolation of the u data versus time
uf = interp1d(t,u)
def sopdt(x,t,uf,Kp,taus,zeta,thetap):
# Kp = process gain
# taus = second order time constant
# zeta = damping factor
# thetap = model time delay
# ts^2 dy2/dt2 + 2 zeta taus dydt + y = Kp u(t-thetap)
# time-shift u
try:
if (t-thetap) <= 0:
um = uf(0.0)
else:
um = uf(t-thetap)
except:
# catch any error
um = u0
# two states (y and y')
y = x[0] - y0
dydt = x[1]
dy2dt2 = (-2.0*zeta*taus*dydt - y + Kp*(um-u0))/taus**2
return [dydt,dy2dt2]
# simulate model with x=[Km,taum,thetam]
def sim_model(x):
# input arguments
Kp = x[0]
taus = x[1]
zeta = x[2]
thetap = x[3]
# storage for model values
xm = np.zeros((ns,2)) # model
# initial condition
xm[0] = xp0
# loop through time steps
for i in range(0,ns-1):
ts = [t[i],t[i+1]]
inputs = (uf,Kp,taus,zeta,thetap)
# turn off warnings
with warnings.catch_warnings():
warnings.simplefilter("ignore")
# integrate SOPDT model
x = odeint(sopdt,xm[i],ts,args=inputs)
xm[i+1] = x[-1]
y = xm[:,0]
return y
# define objective
def objective(x):
# simulate model
ym = sim_model(x)
# calculate objective
obj = 0.0
for i in range(len(ym)):
obj = obj + (ym[i]-yp[i])**2
# return result
return obj
# initial guesses
p0 = np.zeros(4)
p0[0] = 3 # Kp
p0[1] = 5.0 # taup
p0[2] = 1.0 # zeta
p0[3] = 2.0 # thetap
# show initial objective
print('Initial SSE Objective: ' + str(objective(p0)))
# optimize Kp, taus, zeta, thetap
solution = minimize(objective,p0)
# with bounds on variables
#no_bnd = (-1.0e10, 1.0e10)
#low_bnd = (0.01, 1.0e10)
#bnds = (no_bnd, low_bnd, low_bnd, low_bnd)
#solution = minimize(objective,p0,method='SLSQP',bounds=bnds)
p = solution.x
# show final objective
print('Final SSE Objective: ' + str(objective(p)))
print('Kp: ' + str(p[0]))
print('taup: ' + str(p[1]))
print('zeta: ' + str(p[2]))
print('thetap: ' + str(p[3]))
# calculate model with updated parameters
ym1 = sim_model(p0)
ym2 = sim_model(p)
# plot results
plt.figure()
plt.subplot(2,1,1)
plt.plot(t,ym1,'b-',linewidth=2,label='Initial Guess')
plt.plot(t,ym2,'r--',linewidth=3,label='Optimized SOPDT')
plt.plot(t,yp,'k--',linewidth=2,label='Process Data')
plt.ylabel('Output')
plt.legend(loc='best')
plt.subplot(2,1,2)
plt.plot(t,u,'bx-',linewidth=2)
plt.plot(t,uf(t),'r--',linewidth=3)
plt.legend(['Measured','Interpolated'],loc='best')
plt.ylabel('Input Data')
plt.savefig('results.png')
plt.show()
A. Define which part of the simulated model to minimize
- Incorrect. The model is not minimized. The objective function is minimized as the squared error between the model prediction and the measured data.
B. Return to the solver the sum of squared error between the model and the data as the solver changes the input arguments
- Correct. The objective function can return the sum of squared errors or other measures of success such as the sum of absolute values
C. Provide reasonable initial values
- Incorrect. Initial guess values are provided by the user when the solver is called.
D. Adjust the second order model parameters to align the model prediction with the data
- Incorrect. This is the function of the solver. The objective returns the deviation or sum of square error between the model and the data.
3. Returning -obj in place of obj in the objective function has what effect on the solver?
# define objective
def objective(x):
# simulate model
ym = sim_model(x)
# calculate objective
obj = 0.0
for i in range(len(ym)):
obj = obj + (ym[i]-yp[i])**2
# return result
return obj
def objective(x):
# simulate model
ym = sim_model(x)
# calculate objective
obj = 0.0
for i in range(len(ym)):
obj = obj + (ym[i]-yp[i])**2
# return result
return obj
A. Does not impact the result
- Incorrect. The solver maximizes the objective
B. Produces parameters that are negative
- Incorrect. The solver maximizes the objective with a negative one multiplier. A larger negative objective is a lower value and the solver minimizes by default.
C. It would cause the solver to maximize the sum of squared errors instead of minimizing
- Correct. A negative sign switches from minimize to maximize. Many solvers also have a setting to either minimize or maximize the objective function.
D. The solver does not take a negative objective value
- Incorrect. Solvers can take a negative objective value but the sum of squared errors will always be positive
4. Review for Assignment: How are parallel transfer functions combined?
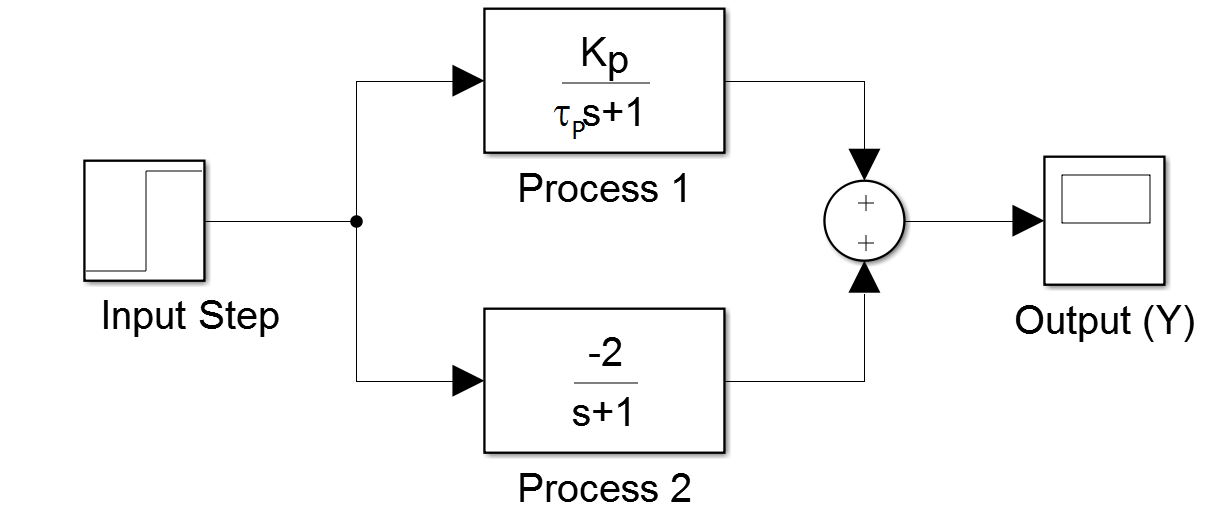
A. Multiplicative
- Incorrect. The output of a transfer function is additive when combined in parallel
B. Additive
- Correct. The output of a transfer function is additive when combined in parallel. It is multiplicative when combined in series.
C. Cannot be combined
- Incorrect. The output of a transfer function is additive when combined in parallel
D. Squared
- Incorrect. The output of a transfer function is additive when combined in parallel
