Derive Transient Balance Equations
 |  |  |  |
|---|
Exercise 1: Mixer Transient Species Balance
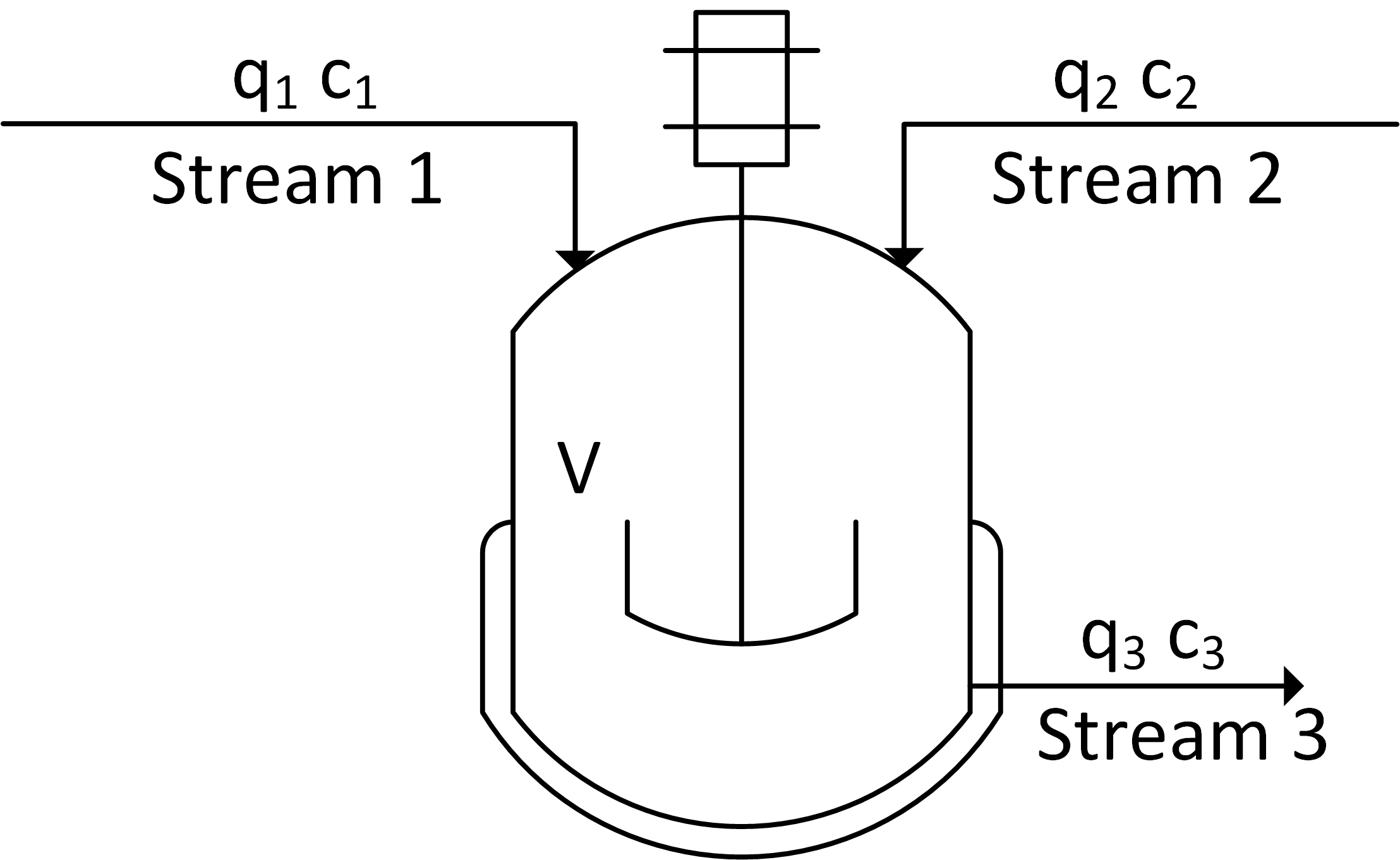
There are two inlet streams to a well-mixed and constant volume vessel. The flow rate is (qi) and concentration is (ci) for all streams (i=1,2,3). Derive a dynamic balance equation for outlet concentration and vessel liquid volume that relates to volumetric flow rates and inlet concentrations. Follow the procedure to build a dynamic model in the modeling introduction. For the model equations, use a transient mass and species balance as shown in balance equations. State any assumptions that are needed. Simplify the equations by eliminating any unnecessary terms and express the final equations in terms of the quantities on the diagram. There is no need to simulate the dynamic response, only derive the form of the equations.
Solution
A species balance for this application starts with the balance equation for moles of A, `n_A`, for two inlet streams and one outlet stream. This is a mixing problem so there is no generation and consumption of species A.
$$\frac{dn_A}{dt} = \dot n_{A1} + \dot n_{A2} - \dot n_{A3}$$
The molar amount, nA is often measured as a concentration, cA, and related by the molar flowrate, q.
$$n_A = c_A \, V \quad \quad \dot n_A = c_A \, q$$
$$\frac{dc_A V}{dt} = c_{A1} q_{1} + c_{A2} q_{2} - c_{A3} q_{3}$$
When the tank is well-mixed, the concentration in the tank is equal to the stream leaving the tank. The chain rule is used to separate the differentials of `V` and `c_{A3}`.
$$\frac{dc_{A3} V}{dt} = V\frac{dc_{A3}}{dt} + c_{A3}\frac{dV}{dt} = c_{A1} q_{1} + c_{A2} q_{2} - c_{A3} q_{3}$$
If the volume is constant then `\frac{dV}{dt}=0` and the expression is simplified to a single ordinary differential equation.
$$V\frac{dc_{A3}}{dt} = c_{A1} q_{1} + c_{A2} q_{2} - c_{A3} q_{3}$$
If the volume is not constant then a mass balance must be added.
$$\frac{dm}{dt} = \dot m_{1} + \dot m_{2} - \dot m_{3}$$
With `m = \rho V` and `\dot m = \rho q` the expression becomes:
$$\rho_3 \frac{dV}{dt} = \rho_1 q_1 + \rho_2 q_2 - \rho_3 q_3$$
If the density `\rho` is constant among all streams then the expression is simplified.
$$\frac{dV}{dt} = q_1 + q_2 - q_3$$
Exercise 2: Mixer Transient Energy Balance
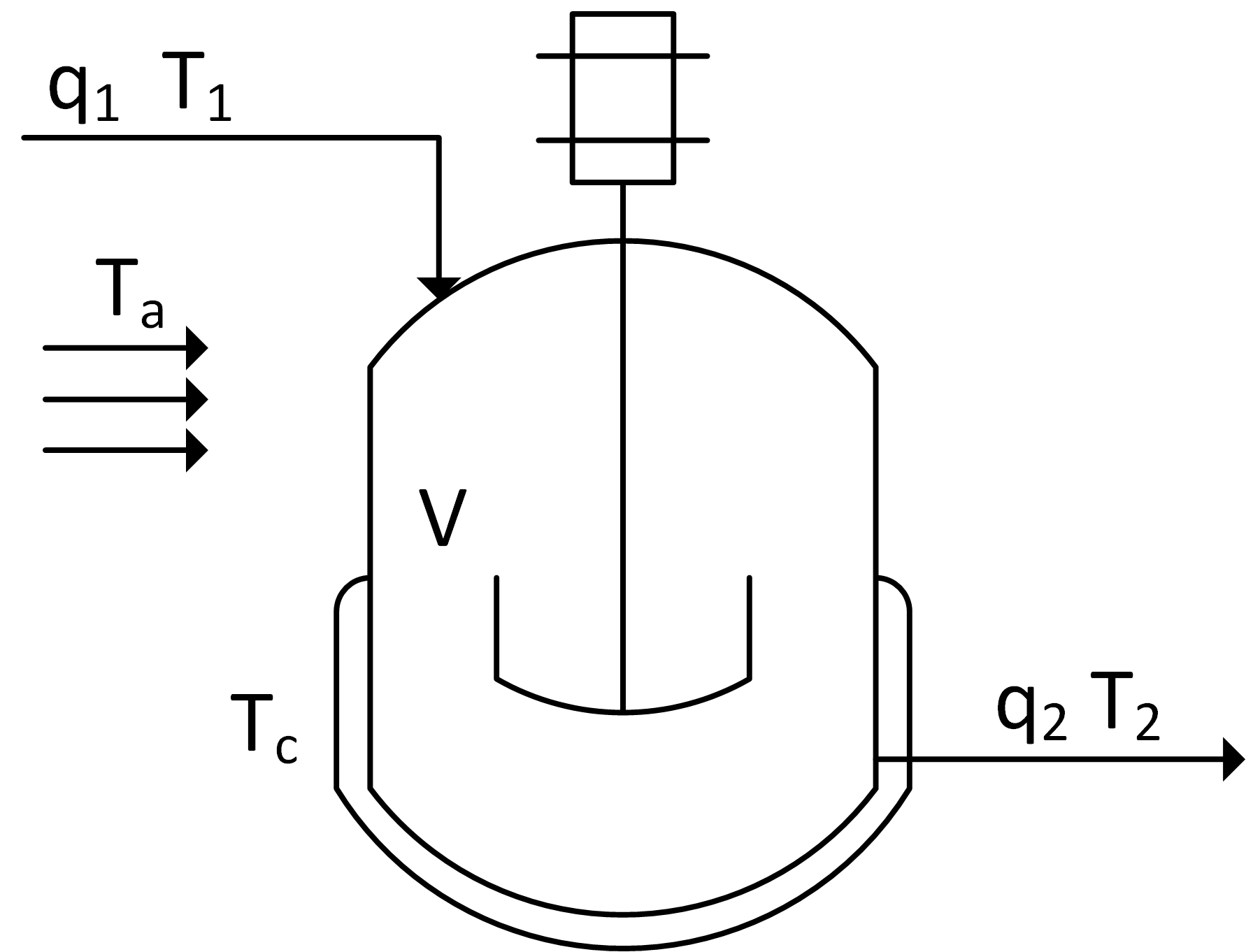
A vessel has one inlet and one outlet stream as shown in the diagram. Derive an expression for the temperature in a vessel. The energy balance should consider heat loss due to convective heat transfer to ambient air at temperature Ta and heat transfer to the cooling jacket fluid at temperature Tc. There is shaft work `W_s` but no chemical reaction. Reduce this energy balance by eliminating any terms and simplifying the expression. The liquid heat capacity and density are constant for all streams.
Solution
An energy balance for this application starts with the balance equation for enthalpy, h.
$$m\,c_p\frac{dT}{dt} = \dot m_{in} c_p \left( T_{in} - T_{ref} \right) - \dot m_{out} c_p \left( T_{out} - T_{ref} \right) + UA \left(T_\infty-T\right) + W_s + r\,V \, \Delta H_r$$
Enthalpy is related to temperature as m cp (T-Tref) where cp is the heat capacity. With a constant reference temperature (Tref), constant mass `m=\rho V`, and equal flows `q=q_1=q_2`, this reduces to the following:
$$\rho V \, c_p \frac{dT}{dt} = \rho \, q \, c_p \left( T_{1} - T_{2} \right) + UA_{c} \left( T_c-T_2 \right) + UA_{a} \left( T_a-T_2 \right) + W_s + r\,V \, \Delta H_r$$
If the volume is not constant then a chain rule must be used to account for the non-zero derivative of volume. Also, the inlet flow and outlet flows are no longer equal `q_1 \ne q_2`. There is no reaction so the heat generated by reaction is zero.
$$\rho V \, c_p \frac{dT}{dt} + \rho T \, c_p \frac{dV}{dt} = \rho \, q_1 \, c_p \left( T_{1} - T_{ref} \right) - \rho \, q_2 \, c_p \left( T_{2} - T_{ref} \right) \\+ UA_{c} \left( T_c-T_2 \right) + UA_{a} \left( T_a-T_2 \right) + W_s$$
If the volume is not constant then a mass balance must also be added.
$$\frac{dm}{dt} = \dot m_{1} - \dot m_{2}$$
With `m = \rho V` and `\dot m = \rho q` the expression becomes:
$$\rho_2 \frac{dV}{dt} = \rho_1 q_1 - \rho_2 q_2$$
If the density `\rho` is constant for the inlet and outlet streams then the expression is simplified.
$$\frac{dV}{dt} = q_1 - q_2$$
TCLab Exercise
See TCLab Convective Heat Transfer