Two Bar Truss Design
Main.TwoBarTruss History
Hide minor edits - Show changes to markup
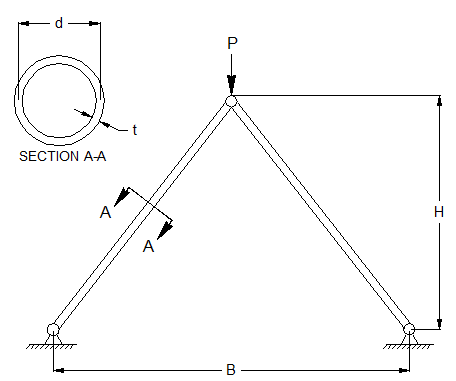
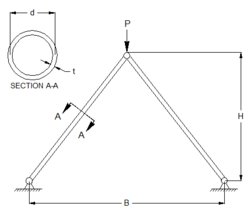
A two-bar truss is a type of truss structure consisting of two bars connected at the ends by either pins or joints. This type of truss is commonly used in construction and engineering applications.
try:
from gekko import GEKKO
except:
# pip install gekko
import pip
pip.main(['install','gekko'])
from gekko import GEKKO
from gekko import GEKKO
(:html:)
<div id="disqus_thread"></div>
<script type="text/javascript">
/* * * CONFIGURATION VARIABLES: EDIT BEFORE PASTING INTO YOUR WEBPAGE * * */
var disqus_shortname = 'apmonitor'; // required: replace example with your forum shortname
/* * * DON'T EDIT BELOW THIS LINE * * */
(function() {
var dsq = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
(document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(dsq);
})();
</script>
<noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
<a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>
(:htmlend:)
Python (GEKKO) Solution
GEKKO is optimization software for mixed-integer and differential algebraic equations. It is coupled with large-scale solvers for linear, quadratic, nonlinear, and mixed integer programming (LP, QP, NLP, MILP, MINLP).
Python (GEKKO) Solution
GEKKO is optimization software for mixed-integer and differential algebraic equations. It is coupled with large-scale solvers for linear, quadratic, nonlinear, and mixed integer programming (LP, QP, NLP, MILP, MINLP).
<iframe width="560" height="315" src="https://www.youtube.com/embed/ah-Cbrim93I" frameborder="0" allowfullscreen></iframe>
<iframe width="560" height="315" src="https://www.youtube.com/embed/ah-Cbrim93I" frameborder="0" allowfullscreen></iframe>
<iframe width="560" height="315" src="https://www.youtube.com/embed/uOTdLfvgYHU" frameborder="0" allowfullscreen></iframe>
<iframe width="560" height="315" src="https://www.youtube.com/embed/uOTdLfvgYHU" frameborder="0" allowfullscreen></iframe>
<iframe width="560" height="315" src="https://www.youtube.com/embed/GB0NYz-k8ZM?rel=0" frameborder="0" allowfullscreen></iframe>
<iframe width="560" height="315" src="https://www.youtube.com/embed/GB0NYz-k8ZM?rel=0" frameborder="0" allowfullscreen></iframe>
dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
<noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
<a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>
<noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
<a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>
<iframe width="560" height="315" src="https://www.youtube.com/embed/ah-Cbrim93I" frameborder="0" allowfullscreen></iframe>
<iframe width="560" height="315" src="https://www.youtube.com/embed/KwELgUu1u-E" frameborder="0" allow="autoplay; encrypted-media" allowfullscreen></iframe>
APM MATLAB Tutorial
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/uOTdLfvgYHU" frameborder="0" allowfullscreen></iframe> (:htmlend:)
APM Python Tutorial
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/ah-Cbrim93I" frameborder="0" allowfullscreen></iframe> (:htmlend:)
APM MATLAB Tutorial
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/uOTdLfvgYHU" frameborder="0" allowfullscreen></iframe> (:htmlend:)
Python (GEKKO) Solution
GEKKO is optimization software for mixed-integer and differential algebraic equations. It is coupled with large-scale solvers for linear, quadratic, nonlinear, and mixed integer programming (LP, QP, NLP, MILP, MINLP).
Python (GEKKO) Solution
GEKKO is optimization software for mixed-integer and differential algebraic equations. It is coupled with large-scale solvers for linear, quadratic, nonlinear, and mixed integer programming (LP, QP, NLP, MILP, MINLP).
GEKKO is optimization software for mixed-integer and differential algebraic equations. It is coupled with large-scale solvers for linear, quadratic, nonlinear, and mixed integer programming (LP, QP, NLP, MILP, MINLP).

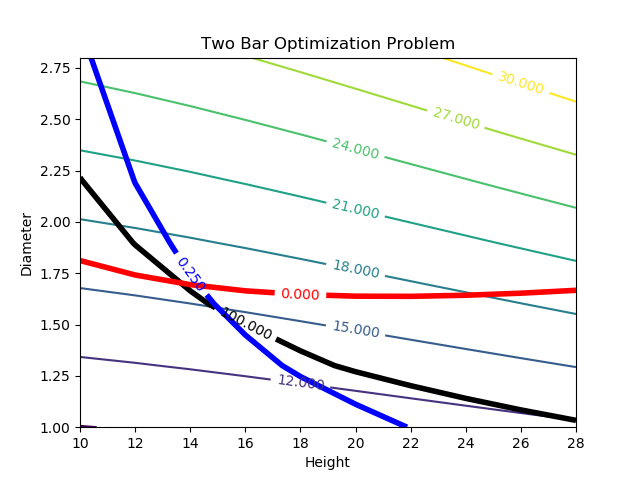
Generate Contour Plot (Python)
Solution Contour Plot (Python)
Python Generates Contour Plots
Generate Contour Plot (Python)
(:sourceend:)
Python Generates Contour Plots
(:source lang=python:)
Python Tutorial
APM Python Tutorial
MATLAB Tutorial
APM MATLAB Tutorial
Python (GEKKO) Solution
(:source lang=python:) import numpy as np
- import gekko, pip install if needed
try:
from gekko import GEKKO
except:
# pip install gekko
import pip
pip.main(['install','gekko'])
from gekko import GEKKO
- create new model
m = GEKKO()
- declare model parameters
width = m.Param(value=60) thickness = m.Param(value=0.15) density = m.Param(value=0.3) modulus = m.Param(value=30000) load = m.Param(value=66)
- declare variables and initial guesses
height = m.Var(value=30.00,lb=10.0,ub=50.0) diameter = m.Var(value=3.00,lb=1.0,ub=4.0) weight = m.Var()
- intermediate variables with explicit equations
leng = m.Intermediate(m.sqrt((width/2)**2 + height**2)) area = m.Intermediate(np.pi * diameter * thickness) iovera = m.Intermediate((diameter**2 + thickness**2)/8) stress = m.Intermediate(load * leng / (2*area*height)) buckling = m.Intermediate(np.pi**2 * modulus * iovera / (leng**2)) deflection = m.Intermediate(load * leng**3 / (2 * modulus * area * height**2))
- implicit equations
m.Equation(weight==2*density*area*leng) m.Equation(weight < 24) m.Equation(stress < 100) m.Equation(stress < buckling) m.Equation(deflection < 0.25)
- minimize weight
m.Obj(weight)
- solve optimization
m.solve() # remote=False for local solve
print ('') print (-- Results of the Optimization Problem --) print ('Height: ' + str(height.value)) print ('Diameter: ' + str(diameter.value)) print ('Weight: ' + str(weight.value))
- Generate a contour plot
- Import some other libraries that we'll need
- matplotlib and numpy packages must also be installed
import matplotlib import numpy as np import matplotlib.pyplot as plt
- Constants
pi = 3.14159 dens = 0.3 modu = 30000.0 load = 66.0
- Analysis variables
wdth = 60.0 thik = 0.15
- Design variables at mesh points
x = np.arange(10.0, 30.0, 2.0) y = np.arange(1.0, 3.0, 0.3) hght, diam = np.meshgrid(x, y)
- Equations and Constraints
leng = ((wdth/2.0)**2.0 + hght**2)**0.5 area = pi * diam * thik iovera = (diam**2.0 + thik**2.0)/8.0 wght = 2.0 * dens * leng * area strs = load * leng / (2.0 * area * hght) buck = pi**2.0 * modu * iovera / (leng**2.0) defl = load * leng**3.0 / (2.0*modu * area * hght**2.0)
- Create a contour plot
- Visit https://matplotlib.org/examples/pylab_examples/contour_demo.html
- for more examples and options for contour plots
plt.figure()
- Weight contours
CS = plt.contour(hght, diam, wght) plt.clabel(CS, inline=1, fontsize=10)
- Stress<100
CS = plt.contour(hght, diam, strs,[100.0],colors='k',linewidths=[4.0]) plt.clabel(CS, inline=1, fontsize=10)
- Deflection<0.25
CS = plt.contour(hght, diam, defl,[0.25],colors='b',linewidths=[4.0]) plt.clabel(CS, inline=1, fontsize=10)
- Stress-Buckling<0
CS = plt.contour(hght, diam, strs-buck,[0.0],colors='r',linewidths=[4.0]) plt.clabel(CS, inline=1, fontsize=10)
- Add some labels
plt.title('Two Bar Optimization Problem') plt.xlabel('Height') plt.ylabel('Diameter')
- Save the figure as a PNG
plt.savefig('contour1.png')
- Create a new figure to see more detail
plt.figure()
- Weight contours
CS = plt.contour(hght, diam, wght) plt.clabel(CS, inline=1, fontsize=10)
- Stress<100
CS = plt.contour(hght, diam, strs,[90.0,100.0],colors='k',linewidths=[0.5, 4.0]) plt.clabel(CS, inline=1, fontsize=10)
- Deflection<0.25
CS = plt.contour(hght, diam, defl,[0.22,0.25],colors='b',linewidths=[0.5, 4.0]) plt.clabel(CS, inline=1, fontsize=10)
- Stress-Buckling<0
CS = plt.contour(hght, diam, strs-buck,[-5.0,0.0],colors='r',linewidths=[0.5, 4.0]) plt.clabel(CS, inline=1, fontsize=10)
- Add some labels
plt.title('Two Bar Optimization Problem') plt.xlabel('Height') plt.ylabel('Diameter')
- Save the figure as a PNG
plt.savefig('contour2.png')
- Show the plots
plt.show() (:sourceend:)
<iframe width="560" height="315" src="https://www.youtube.com/embed/GB0NYz-k8ZM?rel=0" frameborder="0" allowfullscreen></iframe>
<iframe width="560" height="315" src="https://www.youtube.com/embed/uOTdLfvgYHU" frameborder="0" allowfullscreen></iframe>
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/uOTdLfvgYHU" frameborder="0" allowfullscreen></iframe> (:htmlend:)
Objective Function Plot
One part of the assignment asks you to select width and load as variables for a 3d optimal surface plot and plot the solution of the optimization problem to minimize deflection at each of the width / load combinations. This tutorial example shows how to do this same activity but for the alternative problem of minimizing weight.
var disqus_shortname = 'Two_Bar_Truss_Optimization'; // required: replace example with your forum shortname
var disqus_shortname = 'apmonitor'; // required: replace example with your forum shortname
var disqus_shortname = 'Two Bar Truss Optimization'; // required: replace example with your forum shortname
var disqus_shortname = 'Two_Bar_Truss_Optimization'; // required: replace example with your forum shortname
 This assignment can be completed in collaboration with others. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
This assignment can be completed in collaboration with others. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link. This assignment can be completed in collaboration with others. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
This assignment can be completed in collaboration with others. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.(:html:)
<div id="disqus_thread"></div>
<script type="text/javascript">
/* * * CONFIGURATION VARIABLES: EDIT BEFORE PASTING INTO YOUR WEBPAGE * * */
var disqus_shortname = 'Two Bar Truss Optimization'; // required: replace example with your forum shortname
/* * * DON'T EDIT BELOW THIS LINE * * */
(function() {
var dsq = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
(document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(dsq);
})();
</script>
<noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
<a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>
(:htmlend:)
Python Tutorial
<br>
(:htmlend:)
MATLAB Tutorial
(:html:)
<br> <iframe width="560" height="315" src="https://www.youtube.com/embed/uOTdLfvgYHU" frameborder="0" allowfullscreen></iframe>
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/ah-Cbrim93I" frameborder="0" allowfullscreen></iframe> (:htmlend:)
 This assignment can be completed in collaboration with others. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
This assignment can be completed in collaboration with others. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link. This assignment can be completed in collaboration with others. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
This assignment can be completed in collaboration with others. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.This introductory assignment is designed as a means of demonstrating the optimization capabilities of a number of software packages. Below are tutorials for solving this problem with a number of software tools.
This introductory assignment is designed as a means of demonstrating the optimization capabilities of a number of software packages. Below are tutorials for solving this problem with a number of software tools. Below are a few step-by-step tutorials.
 This assignment can be completed as a collaborative assignment. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
This assignment can be completed as a collaborative assignment. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link. This assignment can be completed in collaboration with others. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
This assignment can be completed in collaboration with others. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.(:title Two Bar Optimization Problem:)
(:title Two Bar Truss Design:)
This assignment can be completed as a collaborative  assignment. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
assignment. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
 This assignment can be completed as a collaborative assignment. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
This assignment can be completed as a collaborative assignment. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.This assignment can be completed as a collaborative  assignment. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
assignment. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
This introductory assignment is designed as a means of demonstrating the optimization capabilities of a number of software packages. Below are tutorials for solving this problem with a number of software tools.
This introductory assignment is designed as a means of demonstrating the optimization capabilities of a number of software packages. Below are tutorials for solving this problem with a number of software tools.
This assignment can be completed as a collaborative  assignment. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
assignment. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
This assignment can be completed as a collaborative  assignment. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
assignment. Additional guidelines on individual, collaborative, and group assignments are provided under the Expectations link.
This introductory assignment is designed as a means of demonstrating the optimization capabilities of a number of software packages. Below are tutorials for solving this problem with a number of software tools.
(:title Two Bar Optimization Problem:) (:keywords nonlinear, optimization, engineering optimization, two-bar optimization, engineering design, interior point, active set, differential, algebraic, modeling language, university course:) (:description Engineering design of a two-bar structure to support a load. Optimization principles are used to design the system.:)
A design of the truss is specified by a unique set of values for the analysis variables: height (H), diameter, (d), thickness (t), separation distance (B), modulus of elasticity (E), and material density (rho). Suppose we are interested in designing a truss that has a minimum weight, will not yield, will not buckle, and does not deflect "excessively,” and so we decide our model should calculate weight, stress, buckling stress and deflection.