Optimization with Python
Main.PythonOptimization History
Hide minor edits - Show changes to markup
plt.plot(x0,y1,'k--',linewidth=2,label=r'$xy=2$')
plt.plot(x0,y1,'k--',linewidth=2,label=r'$xyleq5$')

(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/gec5YQckkE0" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe> (:htmlend:)
These tutorial are examples of using Python Gekko to solve an optimization problem.
These tutorial are examples of using Python Gekko to solve an optimization problem.

(:description Optimization with Linear Programming (LP), Quadratic Programming (QP), Nonlinear Programming (NLP), Mixed Integer Linear Programming (MILP), and Mixed Integer Nonlinear Programming (MINLP) with examples in Python.:)
Engineering optimization platforms in Python are an important tool for engineers in the modern world. They allow engineers to quickly and easily optimize complex engineering problems and tasks, such as design optimization, resource allocation, and route planning.
(:description Optimization with Linear Programming (LP), Quadratic Programming (QP), Nonlinear Programming (NLP), Mixed Integer Linear Programming (MILP), and Mixed Integer Nonlinear Programming (MINLP) with examples in Python.:)
This problem has a nonlinear objective that must be minimized. The variable values at the optimal solution are subject to (s.t.) both equality (=40) and inequality (>=25) constraints. The product of the four variables must be greater than 25 while the sum of squares of the variables must also equal 40. In addition, all variables are constrained between 1 and 5 and the initial guess is $x_0=1$, $x_1=5$, $x_2=5$, and $x_3=1$.
This problem has a nonlinear objective that must be minimized. The variable values at the optimal solution are subject to (s.t.) both equality (=40) and inequality (>=25) constraints. The product of the four variables must be greater than 25 while the sum of squares of the variables must also equal 40. In addition, all variables are constrained between 1 and 5 and the initial guess is x=[1,5,5,1].
✅ Activity: Solve the Linear Programming (LP) Problem
✅ Activity: Solve LP Problem
✅ Activity: Solve the Quadratic Programming (QP) Problem
✅ Activity: Solve QP Problem
✅ Activity: Solve the Nonlinear Programming (NLP) Problem
✅ Activity: Solve NLP Problem
✅ Activity: Solve a Mixed Integer Nonlinear Programming (MINLP) Problem
✅ Activity: Solve MINLP Problem
$\begin{align}\mathrm{maximize} \quad & \frac{1}{2} \left(x^2+y^2\right) -2x+2y \\ \mathrm{subject\;to}\quad & 6x+4y\le24 \\ & x+2y\le6 \\ &-x+y\le1 \\ & 0\le y\le2 \\ & x\ge0 \end{align}$
$$\begin{align}\mathrm{maximize} \quad & \frac{1}{2} \left(x^2+y^2\right) -2x+2y \\ \mathrm{subject\;to}\quad & 6x+4y\le24 \\ & x+2y\le6 \\ &-x+y\le1 \\ & 0\le y\le2 \\ & x\ge0 \end{align}$$
(:html:) <img align=left width=200px src='https://apmonitor.com/wiki/uploads/Main/gekko.png'> (:htmlend:)


(:html:) <img align=left width=500px src='https://apmonitor.com/pdc/uploads/Main/lp_example.png'> (:htmlend:)

Introduction to Engineering Optimization
Introduction to Engineering Optimization
<img align=left width=500px src='https://apmonitor.com/me575/uploads/Main/optimize_with_python.png'>
- \\$100 per unit of product G
- \\$125 per unit of product H
- $100 per unit of product G
- $125 per unit of product H
$$c = [-4,-6]$$ with negatives to convert maximize to minimize form
$$A_{ub} = \begin{bmatrix}2 & 3\\ 1 & 1\end{bmatrix}$ and $b_{ub}=[100,80]$$
$$c = [-4,-6]$$
$$A_{ub} = \begin{bmatrix}2 & 3\\ 1 & 1\end{bmatrix} \quad b_{ub}=[100,80]$$
print solution
- print solution
(:html:) <img align=left width=200px src='https://apmonitor.com/wiki/uploads/Main/gekko.png'> (:htmlend:)

print solution
- print solution
solve LP
- solve LP
visualize solution
- visualize solution
plot constraints
- plot constraints
objective contours
- objective contours
optimal point
- optimal point
Problem data
Quadratic weight coefficients
- Problem data
- Quadratic weight coefficients
Linear weight coefficients
- Linear weight coefficients
Strength coefficients
- Strength coefficients
Strength constraints
- Strength constraints
Initial guess
- Initial guess
Define objective function
- Define objective function
Define constraints
- Define constraints
Define optimization
- Define optimization
print results
- print results
(:html:) <img align=left width=200px src='https://apmonitor.com/wiki/uploads/Main/gekko.png'> (:htmlend:)

print results
- print results
visualize solution
- visualize solution
plot constraints
- plot constraints
objective contours
- objective contours
solve QP
- solve QP
initial guesses
- initial guesses
optimize
- optimize
print solution
- print solution
change initial values
- change initial values
print solution
- print solution
visualize solution
- visualize solution
plot constraints
- plot constraints
objective contours
- objective contours
solve NLP
- solve NLP
Define the objective function
- Define the objective function
Define the constraints
- Define the constraints
Define the bounds
- Define the bounds
Solve
- Solve
Print the results
- Print the results
(:html:) <img align=left width=200px src='https://apmonitor.com/wiki/uploads/Main/gekko.png'> (:htmlend:)

Print the results
- Print the results
✅ Activity: Solve the Mixed Integer Linear Programming (MILP) Problem
$\begin{align}\mathrm{maximize} \quad & x+y \\ \mathrm{subject\;to}\quad & 6x+4y\le24 \\ & x+2y\le6 \\ &-x+y\le1 \\ & 0\le y\le2 \\ & x\ge0 \end{align}$
where x and y are integer values. Use either gekko or scipy to solve the MILP and report the results for x, y, and the objective function value.
There are 3 potential solutions. Find the integer solutions on the contour plot to graphically verify the results.
(:html:) <img align=left width=500px src='https://apmonitor.com/pdc/uploads/Main/lp_example.png'> (:htmlend:)
✅ Activity: Solve an MILP Problem
$$\begin{align}\mathrm{maximize} \quad & x+y \\ \mathrm{subject\;to}\quad & 6x+4y\le24 \\ & x+2y\le6 \\ &-x+y\le1 \\ & 0\le y\le2 \\ & x\ge0 \end{align}$$
where x and y are integer values. Use either gekko or scipy to solve the MILP and report the results for x, y, and the objective function value. There are 3 potential solutions. Find the integer solutions on the contour plot to graphically verify the results.

solve MILP
- solve MILP
create integer variables
- create integer variables
create continuous variable
- create continuous variable
integer variable
- integer variable
create Special Ordered Set variable
- create Special Ordered Set variable
continuous variable
- continuous variable
(:html:) <img src='https://apmonitor.com/pdc/uploads/Main/paper_folding.png' align=left width=500px> (:htmlend:)
lower constraint for box width with tabs
- lower constraint for box width with tabs
(:title Optimization with Python:) (:keywords nonlinear, optimization, engineering optimization, mixed integer, linear, nonlinear, sos1, special ordered sets:) (:description Optimization with Linear Programming (LP), Quadratic Programming (QP), Nonlinear Programming (NLP), Mixed Integer Linear Programming (MILP), and Mixed Integer Nonlinear Programming (MINLP) with examples in Python.:)
Engineering optimization platforms in Python are an important tool for engineers in the modern world. They allow engineers to quickly and easily optimize complex engineering problems and tasks, such as design optimization, resource allocation, and route planning.

 Optimize with Python |
Optimize with Python |  Google Colab
Google ColabIntroduction to Engineering Optimization
Optimization Introduction in the Engineering Optimization online course.
Engineering optimization platforms in Python are an important tool for engineers in the modern world. They allow engineers to quickly and easily optimize complex engineering problems and tasks, such as design optimization, resource allocation, and route planning. This notebook has examples for solving LP, QP, NLP, MILP, and MINLP problems in Python.
- 1️⃣ Linear Programming (LP)
- 2️⃣ Quadratic Programming (QP)
- 3️⃣ Nonlinear Programming (NLP)
- 4️⃣ Mixed Integer Linear Programming (MILP)
- 5️⃣ Mixed Integer Nonlinear Programming (MINLP)
<img align=left width=500px src='https://apmonitor.com/me575/uploads/Main/optimize_with_python.png'>
Install gekko Library
First, install the necessary gekko library for this notebook. The solutions to the examples are with scipy and gekko. Installing packages only needs to occur once and then it is always available in that Python distribution. Jupyter notebook may require a restart of the kernel to make the library accessible for import.
(:source lang=python:) pip install gekko (:sourceend:)
1️⃣ Linear Programming
A company manufactures two products (G and H) and has two resources (X and Y) available.
- Each unit of product G requires 3 units of resource X and 8 units of resource Y
- Each unit of product H requires 6 units of resource X and 4 units of resource Y
- The company has a maximum of 30 units of resource X and 44 units of resource Y available.
- The company wants to maximize profits:
- \\$100 per unit of product G
- \\$125 per unit of product H
Linear programming is an optimization method for solving systems of linear constraints and objectives. This problem is mathematically expressed as:
Maximize `100 G + 125 H`
Subject to:
$$3 G + 6 H <= 30$$
$$8 G + 4 H <= 44$$
$$G,H >= 0$$
where G and H are the number of units of products to be produced, respectively.
Scipy Linear Programming
The following code shows how to use linear programming to solve this problem in scipy.optimize with the linprog function. The linear programming problem is placed into the following matrix form:
$$\begin{align}\mathrm{minimize} \quad & c\,x \\ \mathrm{subject\;to}\quad & A \, x=b \\ & A_{ub} \, x<b_{ub} \end{align}$$
with:
$$x = [G,H]$$
$$c = [-4,-6]$$ with negatives to convert maximize to minimize form
$$A_{ub} = \begin{bmatrix}2 & 3\\ 1 & 1\end{bmatrix}$ and $b_{ub}=[100,80]$$
(:source lang=python:) from scipy.optimize import linprog c = [-100, -125] A = 3, 6], [8, 4? b = [30, 44] bound = (0, None) res = linprog(c, A_ub=A, b_ub=b, bounds=[bound, bound], method='highs')
print solution
print(f'Optimal solution: G = {res.x[0]:.2f}, H = {res.x[1]:.2f}') print(f'Maximum profit = $ {-res.fun:.2f}') (:sourceend:)
Gekko Linear Programming
The following code shows how to use linear programming to solve this problem in gekko. There is additional information on solving linear programming problems with sparse or dense matrices in gekko.
(:html:) <img align=left width=200px src='https://apmonitor.com/wiki/uploads/Main/gekko.png'> (:htmlend:)
(:source lang=python:) from gekko import GEKKO m = GEKKO() G,H = m.Array(m.Var,2,lb=0) m.Maximize(100*G+125*H) m.Equation(3*G+6*H<=30) m.Equation(8*G+4*H<=44) m.solve(disp=False)
print solution
print(f'Optimal solution: G = {G.value[0]:.2f}, H = {H.value[0]:.2f}') print(f'Maximum profit = $ {-m.options.objfcnval:.2f}') (:sourceend:)
✅ Activity: Solve the Linear Programming (LP) Problem
$$\begin{align}\mathrm{maximize} \quad & x+y \\ \mathrm{subject\;to}\quad & 6x+4y\le24 \\ & x+2y\le6 \\ &-x+y\le1 \\ & 0\le y\le2 \\ & x\ge0 \end{align}$$
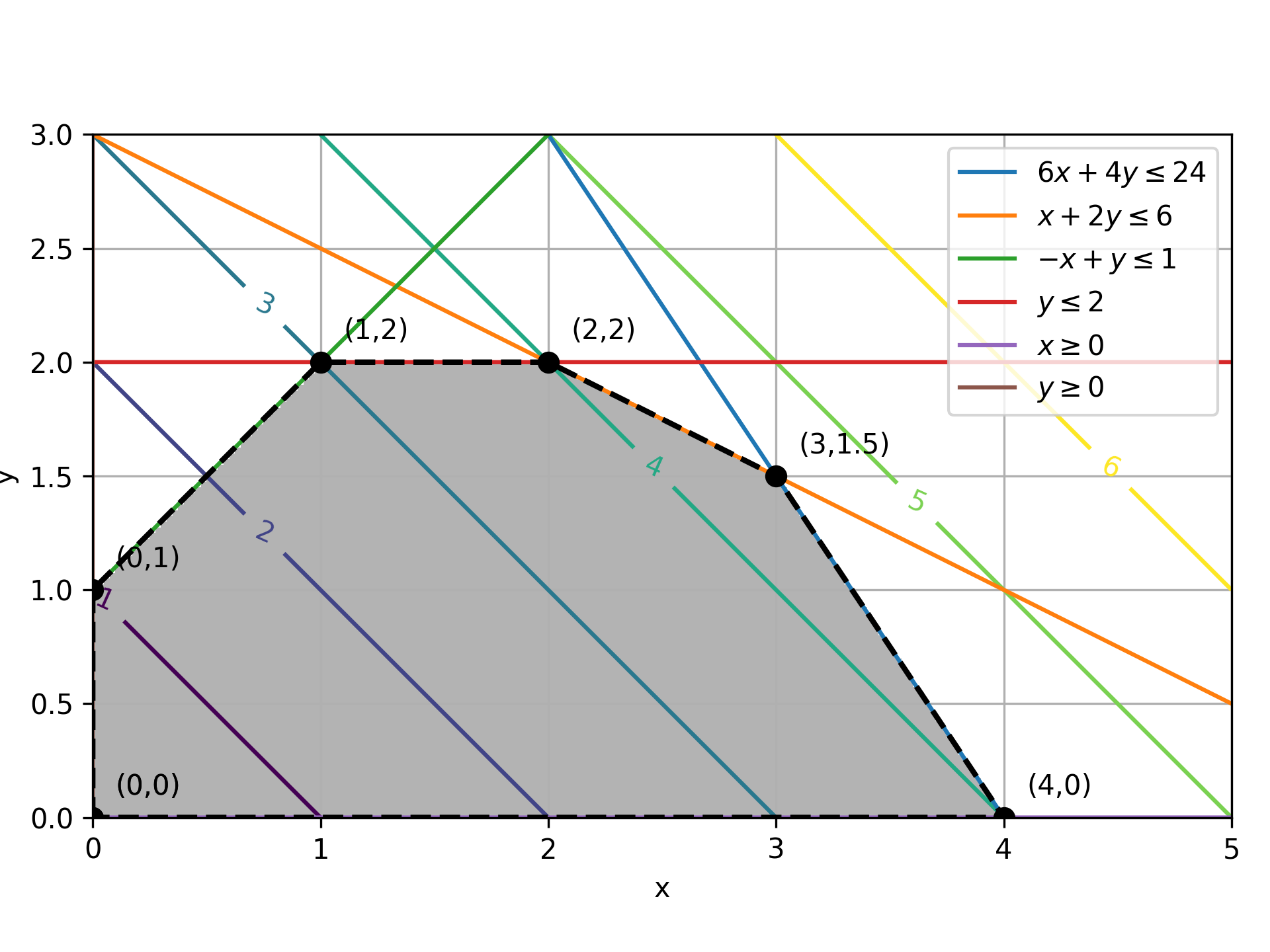
Use either gekko or scipy to solve the LP and report the results for x, y, and the objective function value. Find the solution on the contour plot to graphically verify the results.
(:html:) <img align=left width=500px src='https://apmonitor.com/pdc/uploads/Main/lp_example.png'> (:htmlend:)
LP Solution Help
(:source lang=python:)
solve LP
m = GEKKO(remote=False) x,y = m.Array(m.Var,2,lb=0) m.Equations([6*x+4*y<=24,x+2*y<=6,-x+y<=1,y<=2]) m.Maximize(x+y) m.solve(disp=False) xopt = x.value[0]; yopt = y.value[0] print('x:', xopt,'y:', yopt,'obj:',-m.options.objfcnval) (:sourceend:)
Visualize Solution (Optional)
(:source lang=python:) import numpy as np import matplotlib.pyplot as plt
visualize solution
g = np.linspace(0,5,200) x,y = np.meshgrid(g,g) obj = x+y plt.imshow(((6*x+4*y<=24)&(x+2*y<=6)&(-x+y<=1)&(y<=2)&(x>=0)&(y>=0)).astype(int),
extent=(x.min(),x.max(),y.min(),y.max()),origin='lower',cmap='Greys',alpha=0.3);
plot constraints
x0 = np.linspace(0, 5, 2000) y0 = 6-1.5*x0 # 6*x+4*y<=24 y1 = 3-0.5*x0 # x+2*y<=6 y2 = 1+x0 # -x+y<=1 y3 = (x0*0) + 2 # y <= 2 y4 = x0*0 # x >= 0 plt.plot(x0, y0, label=r'$6x+4y\leq24$') plt.plot(x0, y1, label=r'$x+2y\leq6$') plt.plot(x0, y2, label=r'$-x+y\leq1$') plt.plot(x0, 2*np.ones_like(x0), label=r'$y\leq2$') plt.plot(x0, y4, label=r'$x\geq0$') plt.plot([0,0],[0,3], label=r'$y\geq0$') xv = [0,0,1,2,3,4,0]; yv = [0,1,2,2,1.5,0,0] plt.plot(xv,yv,'ko--',markersize=7,linewidth=2) for i in range(len(xv)):
plt.text(xv[i]+0.1,yv[i]+0.1,f'({xv[i]},{yv[i]})')
objective contours
CS = plt.contour(x,y,obj,np.arange(1,7)) plt.clabel(CS, inline=1, fontsize=10)
optimal point
plt.plot([xopt],[yopt],marker='o',color='orange',markersize=10) plt.xlim(0,5); plt.ylim(0,3); plt.grid(); plt.tight_layout() plt.legend(loc=1); plt.xlabel('x'); plt.ylabel('y') plt.show() (:sourceend:)
2️⃣ Quadratic Programming
A car manufacturer wants to minimize the weight of a car while maintaining a minimum strength requirement. The weight of the car is modeled as a quadratic function of the thickness of the car frame components. The strength of the car is modeled as a linear function of the thickness of the car frame components. The manufacturer wants to minimize the weight of the car while maintaining a minimum strength requirement. This problem is formulated as:
Minimize `\frac{1}{2} x^T Q x + p x`
Subject to:
$$G \, x >= h$$
where x is the thickness of the car frame components, Q is the quadratic weight coefficient matrix, p is the linear weight coefficient vector, G is the strength coefficient matrix, and h is the strength constraint vector.
(:source lang=python:)
Problem data
Quadratic weight coefficients
Q = np.array(1, 0], [0, 2?)
Linear weight coefficients
p = np.array([1, 2])
Strength coefficients
G = np.array(1, 1], [1, 2], [2, 1?)
Strength constraints
h = np.array([3, 4, 5])
Initial guess
x0 = np.array([0, 0]) (:sourceend:)
Scipy Quadratic Programming
The minimize function in the scipy.optimize module is a general-purpose nonlinear optimization routine that can be used to find the minimum of a scalar function of one or more variables. To use it, you need to provide the following inputs:
(:source lang=python:) res = minimize(objective_function, x0,
constraints=con,bounds=bnds,
method='SLSQP',options=opt)
(:sourceend:)
- Objective function: This should be a Python function that has decision variables as inputs and returns a scalar value to be minimized.
- The initial guess for the variables: This should be an array of initial guesses for the variables.
- Constraints with any inequality and equality bounds in residual format.
- Bounds: upper and lower bounds on the decision variables.
- Method: This is an optional parameter that specifies the optimization algorithm.
- Options: Configure parameters for solving the optimization problem.
(:source lang=python:) from scipy.optimize import minimize
Define objective function
def objective_function(x):
return 0.5 * x @ Q @ x + p @ x
Define constraints
def constraint(x):
return G @ x - h
Define optimization
con = {'type': 'ineq', 'fun': constraint} b = (0,10); bnds = (b,b) opt = {'maxiter':1000} res = minimize(objective_function, x0,
constraints=con,bounds=bnds,
method='SLSQP',options=opt)
print results
print(f'Optimal solution: x = {res.x}') print(f'Minimum weight = {res.fun}') (:sourceend:)
Gekko Quadratic Programming
The following code shows how to use quadratic programming in gekko. Change to remote=False to solve locally instead of using the public compute server. The public server has additional solver options.
(:html:) <img align=left width=200px src='https://apmonitor.com/wiki/uploads/Main/gekko.png'> (:htmlend:)
(:source lang=python:) m = GEKKO(remote=False) x = m.Array(m.Var,2,lb=0,ub=10) m.Minimize(0.5 * x@Q@x + p@x) gx = G@x m.Equations([gx[i]>=h[i] for i in range(len(h))]) m.solve(disp=False)
print results
print(f'Optimal solution: x = {x}') print(f'Minimum weight = {m.options.objfcnval}') (:sourceend:)
✅ Activity: Solve the Quadratic Programming (QP) Problem
$\begin{align}\mathrm{maximize} \quad & \frac{1}{2} \left(x^2+y^2\right) -2x+2y \\ \mathrm{subject\;to}\quad & 6x+4y\le24 \\ & x+2y\le6 \\ &-x+y\le1 \\ & 0\le y\le2 \\ & x\ge0 \end{align}$
Use either gekko or scipy to solve the QP and report the results for x, y, and the objective function value.
Visualize QP Objective and Constraints
(:source lang=python:)
visualize solution
g = np.linspace(0,5,200) x,y = np.meshgrid(g,g) obj = 0.5*(x**2+y**2)-2*x+2*y plt.imshow(((6*x+4*y<=24)&(x+2*y<=6)&(-x+y<=1)&(y<=2)&(x>=0)&(y>=0)).astype(int),
extent=(x.min(),x.max(),y.min(),y.max()),origin='lower',cmap='Greys',alpha=0.3);
plot constraints
x0 = np.linspace(0, 5, 2000) y0 = 6-1.5*x0 # 6*x+4*y<=24 y1 = 3-0.5*x0 # x+2*y<=6 y2 = 1+x0 # -x+y<=1 y3 = (x0*0) + 2 # y <= 2 y4 = x0*0 # x >= 0 plt.plot(x0, y0, label=r'$6x+4y\leq24$') plt.plot(x0, y1, label=r'$x+2y\leq6$') plt.plot(x0, y2, label=r'$-x+y\leq1$') plt.plot(x0, 2*np.ones_like(x0), label=r'$y\leq2$') plt.plot(x0, y4, label=r'$x\geq0$') plt.plot([0,0],[0,3], label=r'$y\geq0$') xv = [0,0,1,2,3,4,0]; yv = [0,1,2,2,1.5,0,0] plt.plot(xv,yv,'ko--',markersize=7,linewidth=2) for i in range(len(xv)):
plt.text(xv[i]+0.1,yv[i]+0.1,f'({xv[i]},{yv[i]})')
objective contours
CS = plt.contour(x,y,obj,np.arange(1,7)) plt.clabel(CS, inline=1, fontsize=10) plt.xlim(0,5); plt.ylim(0,3); plt.grid(); plt.tight_layout() plt.legend(loc=1); plt.xlabel('x'); plt.ylabel('y') plt.show() (:sourceend:)
QP Solution Help
(:source lang=python:)
solve QP
m = GEKKO(remote=False) x,y = m.Array(m.Var,2,lb=0) m.Equations([6*x+4*y<=24,x+2*y<=6,-x+y<=1,y<=2]) m.Maximize(0.5*(x**2+y**2)-2*x+2*y) m.solve(disp=False) xopt = x.value[0]; yopt = y.value[0] print('x:', xopt,'y:', yopt,'obj:',-m.options.objfcnval) (:sourceend:)
3️⃣ Nonlinear Programming
A nonlinear optimization problem is the Hock Schittkowski problem 71.
$$\min x_0 x_3 \left(x_0 + x_1 + x_2\right) + x_2$$
$$\mathrm{s.t.} \quad x_0 x_1 x_2 x_3 \ge 25$$
$$x_0^2 + x_1^2 + x_2^2 + x_3^2 = 40$$
$$1\le x \le 5$$
$$x_{init} = (1,5,5,1)$$
This problem has a nonlinear objective that must be minimized. The variable values at the optimal solution are subject to (s.t.) both equality (=40) and inequality (>=25) constraints. The product of the four variables must be greater than 25 while the sum of squares of the variables must also equal 40. In addition, all variables are constrained between 1 and 5 and the initial guess is $x_0=1$, $x_1=5$, $x_2=5$, and $x_3=1$.
Scipy Nonlinear Programming
(:source lang=python:) from scipy.optimize import minimize
def objective(x):
return x[0]*x[3]*(x[0]+x[1]+x[2])+x[2]
def constraint1(x):
return x[0]*x[1]*x[2]*x[3]-25.0
def constraint2(x):
sum_eq = 40.0
for i in range(4):
sum_eq = sum_eq - x[i]**2
return sum_eq
initial guesses
x0 = [1,5,5,1]
optimize
b = (1.0,5.0) bnds = (b, b, b, b) con1 = {'type': 'ineq', 'fun': constraint1} con2 = {'type': 'eq', 'fun': constraint2} cons = ([con1,con2]) solution = minimize(objective,x0,method='SLSQP', bounds=bnds,constraints=cons) x = solution.x
print solution
print('Objective: ' + str(objective(x))) print('Solution:',x) (:sourceend:)
Gekko Nonlinear Programming
The following code shows how to solve nonlinear programming problems in gekko. All solvers in gekko can solve LP, QP, and NLP problems.
(:html:) <img align=left width=200px src='https://apmonitor.com/wiki/uploads/Main/gekko.png'> (:htmlend:)
(:source lang=python:) from gekko import GEKKO import numpy as np m = GEKKO(remote=False) x = m.Array(m.Var,4,value=1,lb=1,ub=5) x1,x2,x3,x4 = x
change initial values
x2.value = 5; x3.value = 5 m.Equation(x1*x2*x3*x4>=25) m.Equation(x1**2+x2**2+x3**2+x4**2==40) m.Minimize(x1*x4*(x1+x2+x3)+x3) m.solve(disp=False)
print solution
print('Objective: ',m.options.OBJFCNVAL) print('Solution: ', x) (:sourceend:)
✅ Activity: Solve the Nonlinear Programming (NLP) Problem
$$\begin{align}\mathrm{minimize} \quad & xy^2-x^2-y^2 \\ \mathrm{subject\;to}\quad & x+y\ge4 \\ & xy<=5 \\ & 1\le x\le3 \\ & 2\le y\le3 \end{align}$$
Use either gekko or scipy to solve the NLP and report the results for x, y, and the objective function value.
Visualize NLP Objective and Constraints
(:source lang=python:)
visualize solution
g = np.linspace(1,3,200) h = np.linspace(2,3,200) x,y = np.meshgrid(g,h) obj = x*y**2-x**2-y**2 plt.imshow(((x+y>=4)&(x*y<=5)&(x>=0)&(y>=0)).astype(int),
extent=(x.min(),x.max(),y.min(),y.max()),origin='lower',cmap='Greys',alpha=0.3);
plot constraints
x0 = np.linspace(1,3,2000)
y0 = 4-x0 # x+y>=4 y1 = 5.0/x0 # x*y<=5
plt.plot(x0,y0,':',color='orange',linewidth=2,label=r'$x+y\geq4$') plt.plot(x0,y1,'k--',linewidth=2,label=r'$xy=2$')
plt.plot([1,1],[2,3],'b-',label=r'$x\geq1$') plt.plot([3,3],[2,3],'b:',label=r'$x\leq3$') plt.plot([1,3],[2,2],'k-',label=r'$y\geq2$') plt.plot(x0, 3*np.ones_like(x0),'k:',label=r'$y\leq3$')
objective contours
CS = plt.contour(x,y,obj,np.round(np.linspace(0,10,21),1)) plt.clabel(CS, inline=1, fontsize=10) plt.xlim(0.9,3.1); plt.ylim(1.9,3.1); plt.grid(); plt.tight_layout() plt.legend(loc=1); plt.xlabel('x'); plt.ylabel('y') plt.show() (:sourceend:)
NLP Solution Help
(:source lang=python:)
solve NLP
m = GEKKO(remote=False) x,y = m.Array(m.Var,2,lb=1,ub=3) y.LOWER=2 m.Minimize(x*y**2-x**2-y**2) m.Equations([x+y>=4,x*y<=5]) m.solve(disp=False) xopt = x.value[0]; yopt = y.value[0] print('x:', xopt,'y:', yopt,'obj:',-m.options.objfcnval) (:sourceend:)
4️⃣ Mixed Integer Linear Programming
Mixed integer linear programming (MILP) is a type of optimization problem that involves both continuous and discrete (integer) variables. In contrast, regular linear programming (LP) only involves continuous variables. The presence of integer variables in MIP makes the problem more difficult to solve, as the solution space is now discrete rather than continuous. This means that many of the techniques used for solving LP problems are not applicable to MIP. Specialized algorithms and solvers, such as branch-and-bound and branch-and-cut, are typically used to solve MIP problems.
Scipy Mixed Integer Linear Programming
Use the integrality option in the linprog function to specify:
- 0: continuous
- 1: integer
(:source lang=python:) from scipy.optimize import linprog
Define the objective function
c = [-1, 4] # minimize -x + 4y
Define the constraints
A_u = np.array(3, 2], [1, 5?) b_u = np.array([10,10])
Define the bounds
b = (0, 10) # 0 <= x <= 10
Solve
res = linprog(c, A_ub=A_u, b_ub=b_u, bounds=(b,b),
integrality=[1,1])
Print the results
print("Objective function: ", res.fun) print("Optimal solution: ", res.x) (:sourceend:)
Gekko Mixed Integer Linear Programming
The following code shows how to solve mixed integer linear programming problems. Use integer=True to specify an integer variable. The solver APOPT is a mixed integer solver in gekko that is selected with m.options.SOLVER=1.
(:html:) <img align=left width=200px src='https://apmonitor.com/wiki/uploads/Main/gekko.png'> (:htmlend:)
(:source lang=python:) m = GEKKO(remote=False) x = m.Array(m.Var,2,lb=0,ub=10,integer=True) m.Minimize(c@x) Ax = A_u@x m.Equations([Ax[i]<=b_u[i] for i in range(len(b_u))]) m.options.SOLVER=1 m.solve(disp=False)
Print the results
print("Objective function: ", m.options.objfcnval) print("Optimal solution: ", x) (:sourceend:)
✅ Activity: Solve the Mixed Integer Linear Programming (MILP) Problem
$\begin{align}\mathrm{maximize} \quad & x+y \\ \mathrm{subject\;to}\quad & 6x+4y\le24 \\ & x+2y\le6 \\ &-x+y\le1 \\ & 0\le y\le2 \\ & x\ge0 \end{align}$
where x and y are integer values. Use either gekko or scipy to solve the MILP and report the results for x, y, and the objective function value.
There are 3 potential solutions. Find the integer solutions on the contour plot to graphically verify the results.
(:html:) <img align=left width=500px src='https://apmonitor.com/pdc/uploads/Main/lp_example.png'> (:htmlend:)
MILP Solution Help
(:source lang=python:)
solve MILP
m = GEKKO(remote=False) x,y = m.Array(m.Var,2,lb=0,integer=True) m.Equations([6*x+4*y<=24,x+2*y<=6,-x+y<=1,y<=2]) m.Maximize(x+y) m.solve(disp=False) xopt = x.value[0]; yopt = y.value[0] print('x:', xopt,'y:', yopt,'obj:',-m.options.objfcnval) (:sourceend:)
5️⃣ Mixed Integer Nonlinear Programming
Mixed integer nonlinear programming (MINLP) is like MILP but may have a nonlinear objective and constraints. It also requires specialized solvers such as the APOPT solver in gekko. There is no current MINLP solver for scipy, but that is likely changing in a future release.
(:source lang=python:) from gekko import GEKKO m = GEKKO() # create GEKKO model
create integer variables
x1 = m.Var(integer=True,lb=-5,ub=10) x2 = m.Var(integer=True,lb=-1,ub=2)
create continuous variable
x3 = m.Var(lb=0) m.Minimize(4*x1**2-4*x2*x1**2+x2**2+x1**2-x1+x3**2) m.Equation(x3*x2>=1) m.options.SOLVER = 1 # APOPT solver m.solve(disp=False) print('x1: ' + str(x1.value[0])) print('x2: ' + str(x2.value[0])) print('x3: ' + str(x3.value[0])) (:sourceend:)
In addition to binary (0,1) and integer variables, Special Ordered Sets are also possible to define from a selection of discrete options such as [0.5, 1.15, 2.6, 5.2].
(:source lang=python:) from gekko import GEKKO m = GEKKO() # create GEKKO model
integer variable
x1 = m.Var(integer=True,lb=-5,ub=10)
create Special Ordered Set variable
x2 = m.sos1([0.5, 1.15, 2.6, 5.2])
continuous variable
x3 = m.Var(lb=0) m.Minimize(4*x1**2-4*x2*x1**2+x2**2+x1**2-x1+x3**2) m.Equation(x3*x2>=1) m.options.SOLVER = 1 # APOPT solver m.solve(disp=False) print('x1: ' + str(x1.value[0])) print('x2: ' + str(x2.value[0])) print('x3: ' + str(x3.value[0])) (:sourceend:)
✅ Activity: Solve a Mixed Integer Nonlinear Programming (MINLP) Problem
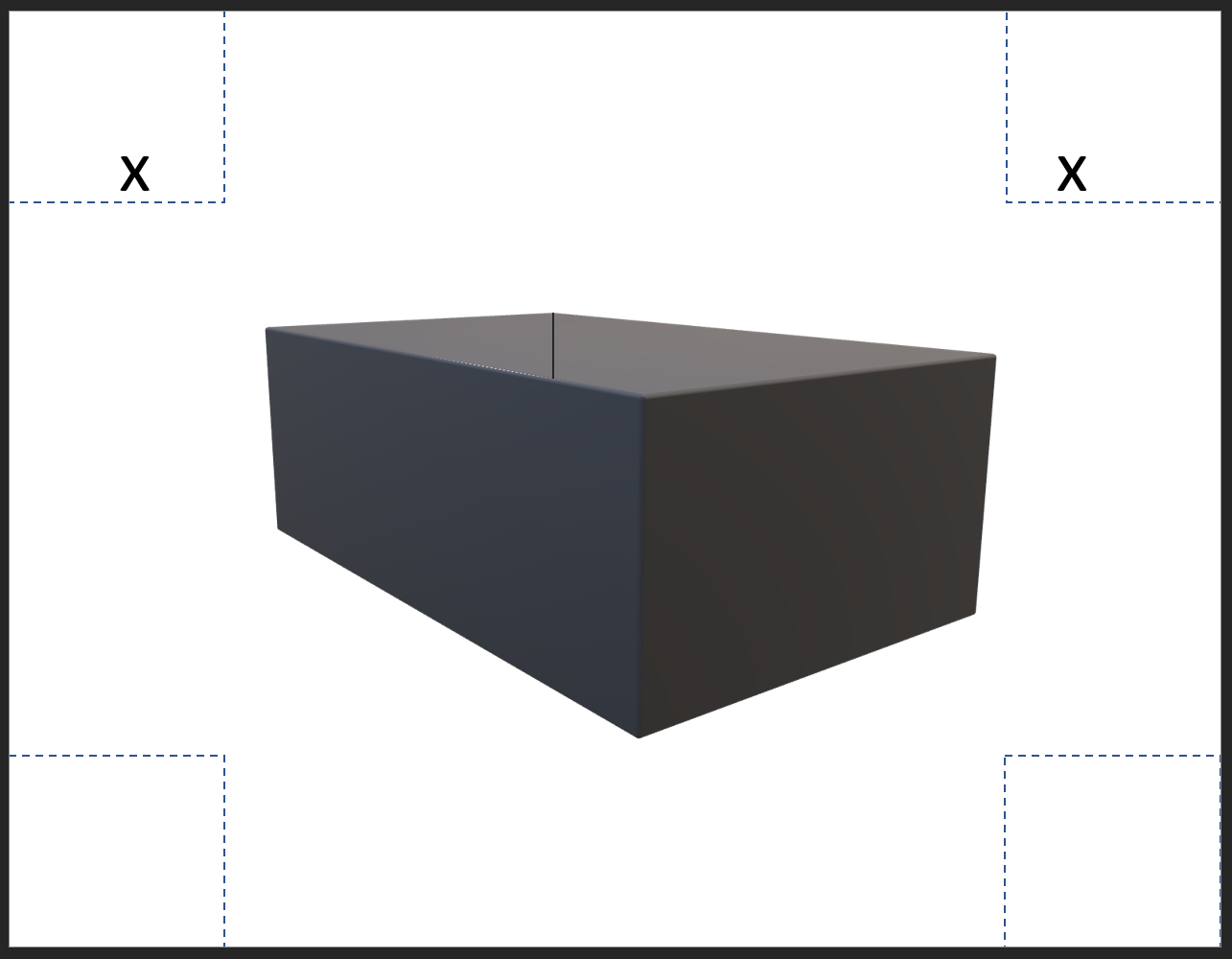
A piece of letter paper 8.5x11 inches is made into an open-top box by first removing the corners and then by folding the sides up to the adjacent side. The starting sheet has height and width. The objective is to maximize the volume of the box (no lid) by choosing an appropriate value of x (the height of the box).
- Print a Box Folding Template (PDF)
- Additional information on paper box folding with solution help.
(:html:) <img src='https://apmonitor.com/pdc/uploads/Main/paper_folding.png' align=left width=500px> (:htmlend:)
Starting with the continuous solution, restrict the height to inch values in integer increments. Below is the continuous solution:
(:source lang=python:) from gekko import GEKKO m = GEKKO(remote=False) paper_width = 8.5 # width of paper paper_length = 11 # length of paper x = m.Var(lb=0) # cut out length box_width = m.Intermediate(paper_width - 2 * x) box_length = m.Intermediate(paper_length - 2 * x) box_height = m.Intermediate(x) Volume = m.Intermediate(box_width * box_length * box_height)
lower constraint for box width with tabs
m.Equations([box_width > 0,box_length > 0,Volume > 0.01]) m.Maximize(Volume) m.options.SOLVER=1 m.solve(disp=False) print('width = ' + str(box_width.value[0])) print('length = ' + str(box_length.value[0])) print('height = ' + str(box_height.value[0])) print('volume = ' + str(Volume.value[0])) (:sourceend:)
Calculate how much the integer solution requirement decreases the volume.
Python Gekko Examples
These tutorial are examples of using Python Gekko to solve an optimization problem.
