Design Optimization

m = GEKKO(remote=False)

(:toggle hide mycode button show="Complete Code":) (:div id=mycode:) (:source lang=python:) from gekko import GEKKO import numpy as np import matplotlib.pyplot as plt

1. Initialize the Gekko model

m = GEKKO(remote=True)

1. Parameters

failure_rate = m.Param(value=0.01) # Failure rate per day cost_maintenance = m.Param(value=1000) # Cost per maintenance cost_failure = m.Param(value=5000) # Cost per failure

1. Variables

interval = m.FV(value=90, lb=30, ub=365) # Maintenance interval (days) interval.STATUS = 1 # Allow optimization

1. Maintenance cost function: Periodic maintenance cost

maintenance_cost = m.Intermediate(cost_maintenance * (365 / interval))

1. Failure cost function: Failures that happen if no maintenance

failures = m.Intermediate(failure_rate * (interval / 2)) # Average failures failure_cost = m.Intermediate(cost_failure * failures)

1. Total cost: Sum of maintenance cost and failure cost

total_cost = m.Var() m.Equation(total_cost==maintenance_cost + failure_cost)

1. Objective: Minimize the total cost

m.Minimize(total_cost)

1. Set solver options

m.options.IMODE = 3 # Steady-state optimization m.options.SOLVER = 1 # APOPT Solver

1. Solve the optimization problem

m.solve(disp=True)

1. Print optimized maintenance interval

opt = interval.value[0] print(f"Optimized maintenance interval: {opt:.2f} days")

1. Create an array of intervals to calculate total costs

intervals = np.linspace(30, 365, 50) total_costs = [] maintenance_costs = [] failure_costs = []

interval.STATUS = 0 for i in intervals:

    interval.value = i
    m.solve(disp=False)  # Solve for each interval value
    total_costs.append(total_cost.value[0])
    maintenance_costs.append(maintenance_cost.value[0])
    failure_costs.append(failure_cost.value[0])

1. Plot total cost vs. interval

plt.figure(figsize=(7, 4)) plt.plot(intervals, total_costs, label='Total Cost') plt.plot(intervals, maintenance_costs, label='Maintenance Cost') plt.plot(intervals, failure_costs, label='Failure Cost') plt.axvline(opt, color='red', linestyle=,

            label=f'Optimized Interval: {opt:.2f} days')

plt.xlabel('Maintenance Interval (days)') plt.ylabel('Total Cost ($)') plt.legend(); plt.grid(True) plt.tight_layout() plt.savefig('total_cost_vs_interval.png', dpi=300) plt.show() (:sourceend:) (:divend:)

plt.figure(figsize=(7, 4))

total_cost = m.Var() m.Equation(total_cost==maintenance_cost + failure_cost)

m.options.SOLVER = 1 # APOPT Solver

opt = interval.value[0] print(f"Optimized maintenance interval: {opt:.2f} days")

1. Create an array of intervals to calculate total costs

intervals = np.linspace(30, 365, 50) total_costs = [] maintenance_costs = [] failure_costs = []

interval.STATUS = 0 for i in intervals:

    interval.value = i
    m.solve(disp=False)  # Solve for each interval value
    total_costs.append(total_cost.value[0])
    maintenance_costs.append(maintenance_cost.value[0])
    failure_costs.append(failure_cost.value[0])

1. Plot total cost vs. interval

plt.figure(figsize=(8, 4)) plt.plot(intervals, total_costs, label='Total Cost') plt.plot(intervals, maintenance_costs, label='Maintenance Cost') plt.plot(intervals, failure_costs, label='Failure Cost') plt.axvline(opt, color='red', linestyle=,

            label=f'Optimized Interval: {opt:.2f} days')

plt.xlabel('Maintenance Interval (days)') plt.ylabel('Total Cost ($)') plt.legend(); plt.grid(True) plt.savefig('total_cost_vs_interval.png', dpi=300) plt.show()

(:title Maintenance Interval Optimization:) (:keywords optimization, maintenance, chemical plant, refinery, engineering, course:) (:description Optimization of Maintenance Intervals in Manufacturing Facilities using Gekko:)

Python Gekko optimization package determines the optimal maintenance intervals in a manufacturing facility to minimize total operational costs. The costs include maintenance costs and failure-related costs when equipment is not maintained on time. The optimization balances between frequent maintenance and reducing downtime due to equipment failure.

Import Libraries: Import the necessary libraries for Gekko and plotting. Install Gekko if not already installed.

(:source lang=python:) from gekko import GEKKO import numpy as np import matplotlib.pyplot as plt

1. Initialize the Gekko model

m = GEKKO() (:sourceend:)

Define Parameters: Set up the parameters for the model such as maintenance costs, failure rate, and failure costs.

(:source lang=python:)

1. Parameters

failure_rate = m.Param(value=0.01) # Failure rate per day cost_maintenance = m.Param(value=1000) # Cost per maintenance cost_failure = m.Param(value=5000) # Cost per failure (:sourceend:)

Define Variables: The maintenance interval is the decision variable to be optimized.

(:source lang=python:)

1. Variables

interval = m.FV(value=90, lb=30, ub=365) # Maintenance interval (days) interval.STATUS = 1 # Allow optimization (:sourceend:)

Define Objective: Create the cost functions and the objective to minimize the total cost.

(:source lang=python:)

1. Maintenance cost function: Periodic maintenance cost

maintenance_cost = m.Intermediate(cost_maintenance * (365 / interval))

1. Failure cost function: Failures that happen if no maintenance

failures = m.Intermediate(failure_rate * (interval / 2)) # Average failures failure_cost = m.Intermediate(cost_failure * failures)

1. Total cost: Sum of maintenance cost and failure cost

total_cost = m.Intermediate(maintenance_cost + failure_cost)

1. Objective: Minimize the total cost

m.Minimize(total_cost) (:sourceend:)

Solve the Optimization Problem: Solve the optimization problem to find the optimal maintenance interval.

(:source lang=python:)

1. Set solver options

m.options.IMODE = 3 # Steady-state optimization

1. Solve the optimization problem

m.solve(disp=True)

1. Print optimized maintenance interval

print(f"Optimized maintenance interval: {interval.value[0]:.2f} days") (:sourceend:)

Results Visualization: Plot the cost breakdown to visualize the optimization result.

(:source lang=python:)

1. Plot the cost breakdown

plt.figure(figsize=(8,4)) plt.bar(['Maintenance Cost', 'Failure Cost'],

        [maintenance_cost.value[0], failure_cost.value[0]])

plt.title('Cost Breakdown'); plt.ylabel('Cost ($)') plt.savefig('cost.png',dpi=300); plt.show() (:sourceend:)

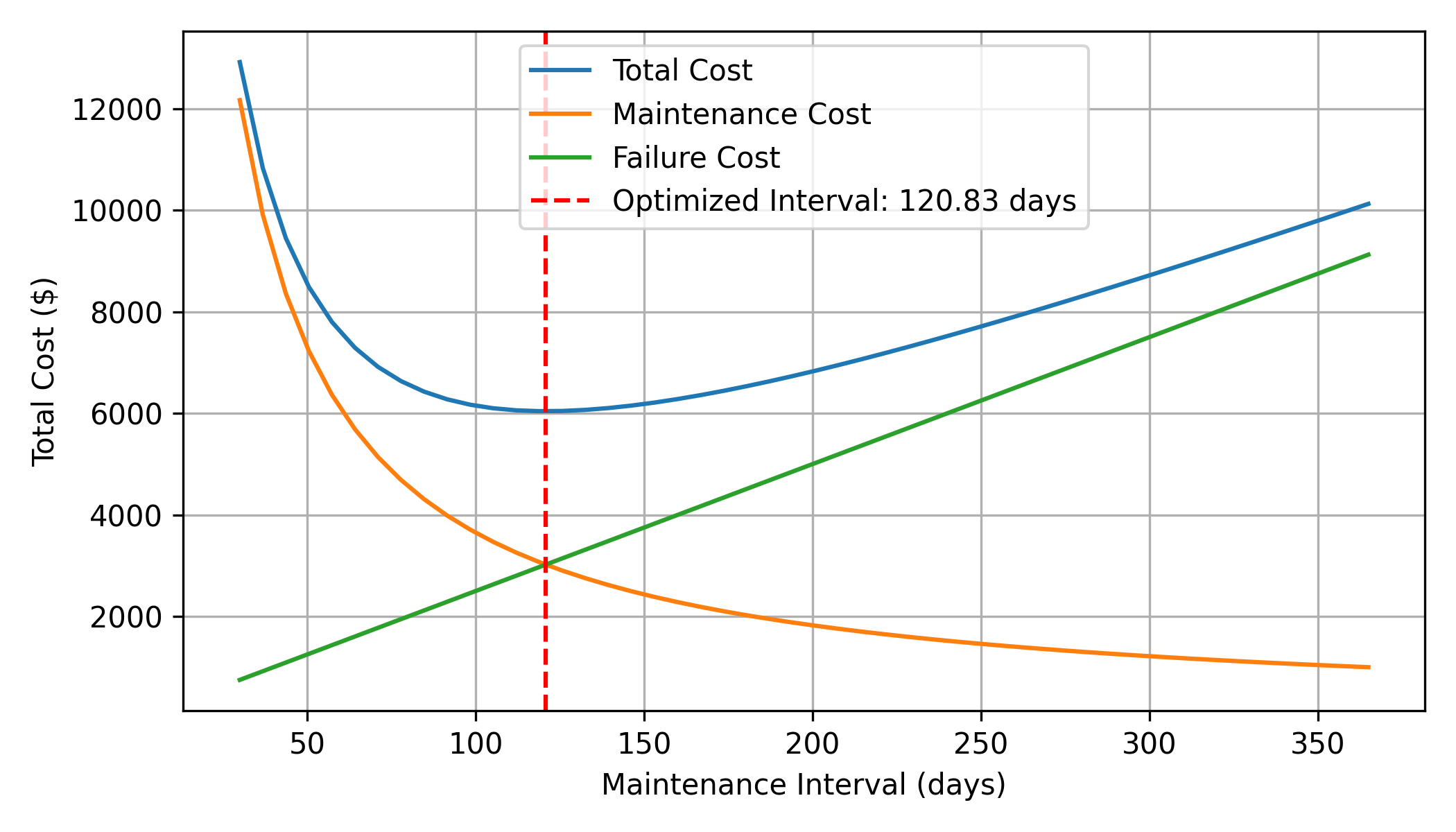
This example demonstrates how to use Gekko to optimize maintenance intervals, balancing the trade-offs between the costs of regular maintenance and potential downtime due to equipment failure. Adjust the parameters such as failure rates, costs, and intervals to fit different industrial scenarios. Turn-around events are much more complex and involve plant-wide maintenance planning during facility shut-down periods. Many maintenance activities are scheduled during those planned outages. For other equipment that doesn't require facility shutdown, regular maintenance schedules can be optimized to trade-off interval with cost of breakdown.

More examples can be found on the Gekko Documentation Page.