Discrete Optimization in Engineering Design
Main.DiscreteOptimization History
Show minor edits - Show changes to markup
m.Obj(4*x1**2-4*x2*x1**2+x2**2+x1**2-x1+1)
m.Minimize(4*x1**2-4*x2*x1**2+x2**2+x1**2-x1+1)
(:html:)
<div id="disqus_thread"></div>
<script type="text/javascript">
/* * * CONFIGURATION VARIABLES: EDIT BEFORE PASTING INTO YOUR WEBPAGE * * */
var disqus_shortname = 'apmonitor'; // required: replace example with your forum shortname
/* * * DON'T EDIT BELOW THIS LINE * * */
(function() {
var dsq = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
(document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(dsq);
})();
</script>
<noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
<a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>
(:htmlend:)
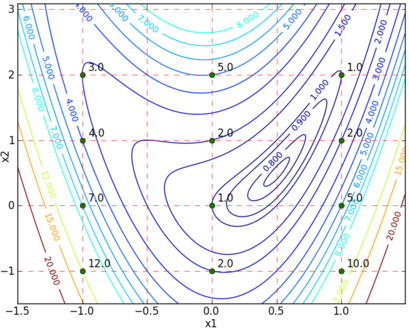
The integer problem can be solved with Python GEKKO. The option integer=True is used to switch the variable from continuous to integer form. The APOPT solver is required to solve problem with integer variables but other solvers such as IPOPT can provide a relaxed solution where the integer conditions are not enforced.
(:source lang=python:) from gekko import GEKKO m = GEKKO() # create GEKKO model
- create integer variables
x1 = m.Var(integer=True,lb=-1,ub=1) x2 = m.Var(integer=True,lb=-1,ub=2) m.Obj(4*x1**2-4*x2*x1**2+x2**2+x1**2-x1+1) m.options.SOLVER = 1 # APOPT solver m.solve() print('x1: ' + str(x1.value[0])) print('x2: ' + str(x2.value[0])) (:sourceend:)
At first glance it might seem solving a discrete variable problem would be easier than a continuous problem. After all, for a variable within a given range, a set of discrete values within the range is finite whereas the number of continuous values is infinite. When searching for an optimum, it seems it would be easier to search from a finite set rather than from an infinite set.
This is not the case, however. Solving discrete problems is harder than continuous problems. This is because of the combinatorial explosion that occurs in all but the smallest problems. For example if we have two variables which can each take 10 values, we have 10*10 = 100 possibilities. If we have 10 variables that can each take 10 values, we have 10^10 possibilities. Even with the fastest computer, it would take a long time to evaluate all of these.
At first glance it might seem solving a discrete variable problem would be easier than a continuous problem. After all, for a variable within a given range, a set of discrete values within the range is finite whereas the number of continuous values is infinite. When searching for an optimum, it seems it would be easier to search from a finite set rather than from an infinite set.
This is not the case, however. Solving discrete problems is harder than continuous problems. This is because of the combinatorial explosion that occurs in all but the smallest problems. For example if we have two variables which can each take 10 values, we have 10*10 = 100 possibilities. If we have 10 variables that can each take 10 values, we have 10^10 possibilities. Even with the fastest computer, it would take a long time to evaluate all of these.
Discrete decision variables are those that have only certain levels or quantities that are acceptable at an optimal solution. Examples of discrete variables are binary (e.g. off/on or 0/1), integer (e.g. 4,5,6,7), or general discrete values that are not integer (e.g. 1/4 cm, 1/2 cm, 1 cm).
(:html:) <iframe width="560" height="315" src="https://www.youtube.com/embed/RPKPjqdiX1c" frameborder="0" allowfullscreen></iframe> (:htmlend:)
(:html:) <iframe width="560" height="315" src="//www.youtube.com/embed/XhqteZIydT0?rel=0" frameborder="0" allowfullscreen></iframe> (:htmlend:)
One often encounters problems in which design variables must be selected from among a set of discrete values. Examples of discrete variables include catalog or standard sizes (I beams, motors, springs, fasteners, pipes, etc.), materials, and variables which are naturally integers such as people, gear teeth, number of shells in a heat exchanger and number of distillation trays in a distillation column. Many engineering problems are discrete in nature.
One often encounters problems in which design variables must be selected from among a set of discrete values. Examples of discrete variables include catalog or standard sizes (I beams, motors, springs, fasteners, pipes, etc.), materials, and variables which are naturally integers such as people, gear teeth, number of shells in a heat exchanger and number of distillation trays in a distillation column. Many engineering problems are discrete in nature.
- Branch and Bound (Select APOPT solver)
- Branch and Bound with APMonitor (Select APOPT solver)
- Branch and Bound with APMonitor
- Branch and Bound (Select APOPT solver)
- Chapter 4: Discrete Optimization
- Lecture 4.1: Introduction to Discrete Optimization
- Branch and Bound with MATLAB
- Branch and Bound with APMonitor
(:html:)
<div id="disqus_thread"></div>
<script type="text/javascript">
/* * * CONFIGURATION VARIABLES: EDIT BEFORE PASTING INTO YOUR WEBPAGE * * */
var disqus_shortname = 'apmonitor'; // required: replace example with your forum shortname
/* * * DON'T EDIT BELOW THIS LINE * * */
(function() {
var dsq = document.createElement('script'); dsq.type = 'text/javascript'; dsq.async = true;
dsq.src = 'https://' + disqus_shortname + '.disqus.com/embed.js';
(document.getElementsByTagName('head')[0] || document.getElementsByTagName('body')[0]).appendChild(dsq);
})();
</script>
<noscript>Please enable JavaScript to view the <a href="https://disqus.com/?ref_noscript">comments powered by Disqus.</a></noscript>
<a href="https://disqus.com" class="dsq-brlink">comments powered by <span class="logo-disqus">Disqus</span></a>
(:htmlend:)
(:title Discrete Optimization in Engineering Design:) (:keywords discrete optimization, nonlinear, optimization, engineering optimization, interior point, active set, differential, algebraic, modeling language, university course:) (:description One often encounters problems in which design variables must be selected from among a set of discrete values:)
Chapter 4: Discrete Optimization
One often encounters problems in which design variables must be selected from among a set of discrete values. Examples of discrete variables include catalog or standard sizes (I beams, motors, springs, fasteners, pipes, etc.), materials, and variables which are naturally integers such as people, gear teeth, number of shells in a heat exchanger and number of distillation trays in a distillation column. Many engineering problems are discrete in nature.
At first glance it might seem solving a discrete variable problem would be easier than a continuous problem. After all, for a variable within a given range, a set of discrete values within the range is finite whereas the number of continuous values is infinite. When searching for an optimum, it seems it would be easier to search from a finite set rather than from an infinite set.
This is not the case, however. Solving discrete problems is harder than continuous problems. This is because of the combinatorial explosion that occurs in all but the smallest problems. For example if we have two variables which can each take 10 values, we have 10*10 = 100 possibilities. If we have 10 variables that can each take 10 values, we have 10^10 possibilities. Even with the fastest computer, it would take a long time to evaluate all of these.