Quiz on State Space Models
 |  |  |  |  |
|---|
1. Why is it an advantage to put equations into state space form?
$$\dot x = A x + B u$$
$$y = C x + D u$$
Select three correct answers.
- Correct. The eigenvalues of the A matrix determine system stability
- Incorrect. State space models are linear
- Correct. The A, B, C, D matrices are the only things needed to express a multiple inputs and multiple outputs in state space form
- Correct. Time-domain models are more intuitive because the states represent underlying process variables that affect the dynamics of the output. There is also a suite of linear systems theory and predictive controllers that have been designed with a state space model as the starting point.
2. Which of the following equations is equivalent to the state space model with A=-5, B=2, C=1, and D=0?
$$\dot x = A x + B u$$
$$y = C x + D u$$
- Incorrect. `{dy}/{dt} = -5y + 2u`
- Incorrect. `{dy}/{dt} = -5y + 2u`
- Correct. Yes
- Incorrect. `{dy}/{dt} = -5y + 2u`
3. Which of the exercises have multiple states?
A. First order differential equation
$$3 \, \frac{dx}{dt} + 12 \, x = 6 \, u$$ $$y = x$$
B. Second order differential equations
$$2 \frac{dx_1}{dt} + 6 \, x_1 = 8 \, u$$ $$3 \frac{dx_2}{dt} + 6 \, x_1 + 9 \, x_2 = 0$$ $$y = \frac{x_1 + x_2}{2}$$
C. Second order differential equation
$$4 \frac{d^2y}{dt^2} + 2 \frac{dy}{dt} + y = 3 \, u$$
D. Nonlinear differential equations
$$2 \frac{dx_1}{dt} + x_1^2 + 3 \, x_2^2 = 16 \, u$$ $$3 \frac{dx_2}{dt} + 6 \, x_1^2 + 6 \, x_2^2 = 0$$ $$y_1 = x_2$$ $$y_2 = x_1$$
$$\bar u = 1, \quad \bar x = \begin{bmatrix}2\\2\end{bmatrix}$$
- Incorrect. This is the only exercise with only one state
- Incorrect. C has two states. It can be reformulated into a system of differential equations.
- Incorrect. C and D have two states (`x_1` and `x_2`)
- Correct. B, C, and D have two states (`x_1` and `x_2`).
4. The A matrix of a state space model has eigenvalues: [0.45+/-2.1i, -3.1].
$$A = \begin{bmatrix} -0.2 & -1 & 0.6\\ 5.0 & 1.0 & -0.7\\ 1.0 & 0 & -3.0 \end{bmatrix}$$
What conclusion can be drawn about the system stability and oscillations?
- Incorrect. There is a non-negative real part of an eigenvalue
- Incorrect. There are imaginary parts to the eigenvalues so there are oscillations. However, there is a positive real part to at least one eigenvalue so the system response diverges and is not stable.
- Correct. There are imaginary parts to the eigenvalues and a positive real part to at least one eigenvalue so the system response diverges and is not stable.Verification
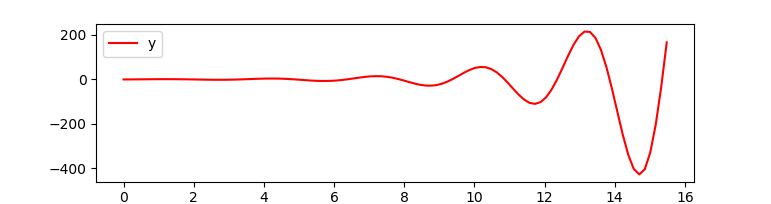import numpy as np
A = [[-0.2,-1,0.6],[5.0,1.0,-0.7],[1.0,0,-3.0]]
B = [[1],[0],[0]]; C = [0.5,0.5,0.5]; D = [0]
print(np.linalg.eig(A)[0])
from scipy import signal
sys1 = signal.StateSpace(A,B,C,D)
t1,y1 = signal.step(sys1)
import matplotlib.pyplot as plt
plt.figure(1)
plt.plot(t1,y1,'r-',label='y')
plt.legend()
plt.xlabel('Time')
plt.show()
- Incorrect. There are imaginary parts to the eigenvalues and a positive real part to at least one eigenvalue so the system response diverges and is not stable.
