Quiz on Second Order Graphical Methods
 |  |  |  |  |
|---|
1. What type of second order system has oscillations?
- Incorrect. Two first order systems do not lead to oscillation but two first order systems in parallel may create an inverse response. Underdamped systems have an oscillatory response to a step change in the input.
- Correct. Underdamped systems have an oscillatory response to a step change in the input
- Incorrect. Underdamped systems have an oscillatory response to a step change in the input
- Incorrect. Underdamped systems have an oscillatory response to a step change in the input
2. What is the relationship between the overshoot ratio (OS) and the decay ratio (DR)?
- Incorrect. `DR = OS^2 = \exp({-2 \pi \zeta}/{\sqrt{1-\zeta^2}})`
- Incorrect. `DR = OS^2 = \exp({-2 \pi \zeta}/{\sqrt{1-\zeta^2}})`
- Incorrect. `DR = OS^2 = \exp({-2 \pi \zeta}/{\sqrt{1-\zeta^2}})`
- Correct. `DR = OS^2 = \exp({-2 \pi \zeta}/{\sqrt{1-\zeta^2}})`
Information for Questions 3 and 4: An underdamped system has an Overshoot ratio (OS) of 0.5 and a peak time `(t_p)` of 0.2 min. The system is described by a second order equation.
$$\tau_s^2 \frac{d^2y}{dt^2} + 2 \zeta \tau_s \frac{dy}{dt} + y = K_p \, u\left(t-\theta_p \right)$$
Overshoot ratio `OS`: amount that first oscillation surpasses the steady state level relative to the steady state change
$$OS = \exp\left({-\frac{\pi \zeta}{\sqrt{1-\zeta^2}}}\right) \quad \quad \quad \zeta = \sqrt{\frac{\left(\ln(OS)\right)^2}{\pi^2 + \left(\ln(OS)\right)^2}}$$
Peak time `t_p`: amount of time to reach the first peak (after accounting for dead time)
$$t_p = \frac{\pi \tau_s}{\sqrt{1-\zeta^2}} \quad \quad \quad \tau_s = \frac{\sqrt{1-\zeta^2}}{\pi}t_p$$
Period `P`: the length of time for an oscillation from peak to peak
$$P = \frac{2 \pi \tau_s}{\sqrt{1-\zeta^2}} \quad \quad \tau_s = \frac{\sqrt{1-\zeta^2}}{2 \pi}P$$
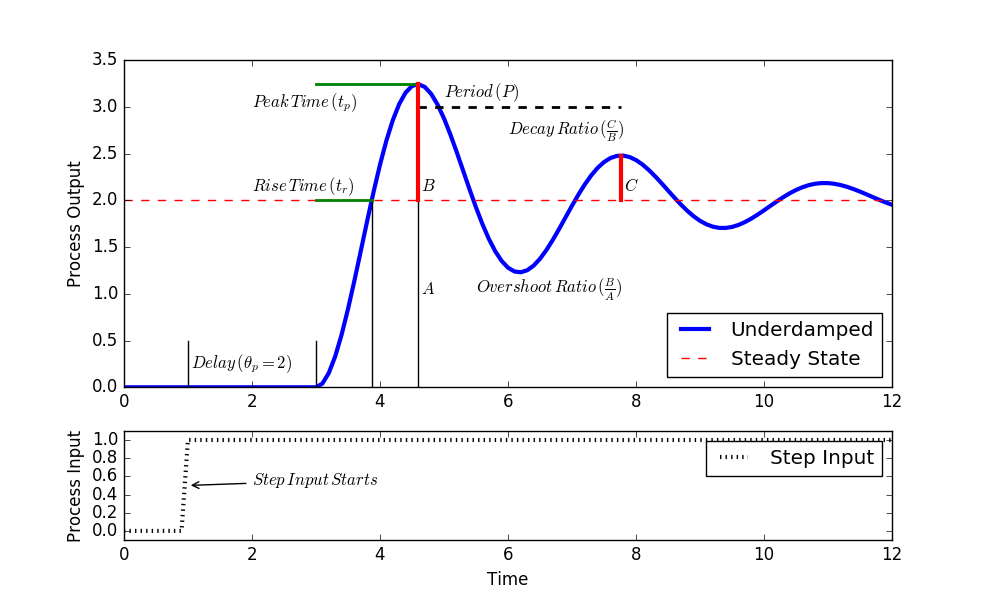
3. What is the value of `\tau_s`?
- Incorrect. Square the `\zeta` in the equation for `\tau_s`
- Incorrect. There is a square root in the equation for `\zeta`
- Incorrect. This is the value for `\zeta`.
$$\zeta = \sqrt{\frac{\left(\ln(0.5)\right)^2}{\pi^2 + \left(\ln(0.5)\right)^2}} = \sqrt{\frac{\left(\ln(0.5)\right)^2}{\pi^2 + \left(\ln(0.5)\right)^2}} = \sqrt{0.0464} = 0.215$$
- Correct.
$$\zeta = \sqrt{\frac{\left(\ln(0.5)\right)^2}{\pi^2 + \left(\ln(0.5)\right)^2}} = \sqrt{\frac{\left(\ln(0.5)\right)^2}{\pi^2 + \left(\ln(0.5)\right)^2}} = \sqrt{0.0464} = 0.215$$
$$\tau_s = \frac{\sqrt{1-\zeta^2}}{\pi}t_p = \frac{\sqrt{1-0.215^2}}{\pi}0.2 = 0.0622$$
4. What is the period of oscillation `P`?
- Correct. `P = {2 \pi \tau_s}/{\sqrt{1-\zeta^2}} = {2 \pi 0.0622}/{\sqrt{1-0.215^2}} = 0.4`
- Incorrect. Use `2\pi` on the top of the fraction
- Incorrect. Square `\zeta`
- Incorrect. The units of time are from the value of `t_p` so seconds is incorrect unless there is a unit conversion to 24 sec = 0.4 min.
