Solve Differential Equations in Python
Differential equations can be solved with different methods in Python. Below are examples that show how to solve differential equations with (1) GEKKO Python, (2) Euler's method, (3) the ODEINT function from Scipy.Integrate. Additional information is provided on using APM Python for parameter estimation with dynamic models and scale-up to large-scale problems.
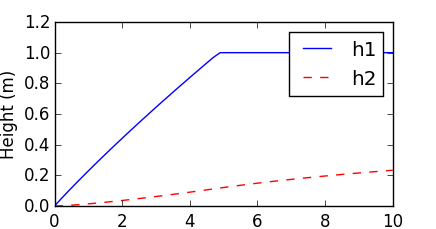
1. GEKKO Python
See Introduction to GEKKO for more information on solving differential equations in Python. GEKKO Python solves the differential equations with tank overflow conditions. When the first tank overflows, the liquid is lost and does not enter tank 2. The model is composed of variables and equations. The differential variables (h1 and h2) are solved with a mass balance on both tanks.
import matplotlib.pyplot as plt
from gekko import GEKKO
m = GEKKO()
# integration time points
m.time = np.linspace(0,10)
# constants
c1 = 0.13
c2 = 0.20
Ac = 2 # m^2
# inflow
qin1 = 0.5 # m^3/hr
# variables
h1 = m.Var(value=0,lb=0,ub=1)
h2 = m.Var(value=0,lb=0,ub=1)
overflow1 = m.Var(value=0,lb=0)
overflow2 = m.Var(value=0,lb=0)
# outflow equations
qin2 = m.Intermediate(c1 * h1**0.5)
qout1 = m.Intermediate(qin2 + overflow1)
qout2 = m.Intermediate(c2 * h2**0.5 + overflow2)
# mass balance equations
m.Equation(Ac*h1.dt()==qin1-qout1)
m.Equation(Ac*h2.dt()==qin2-qout2)
# minimize overflow
m.Obj(overflow1+overflow2)
# set options
m.options.IMODE = 6 # dynamic optimization
# simulate differential equations
m.solve()
# plot results
plt.figure(1)
plt.plot(m.time,h1,'b-')
plt.plot(m.time,h2,'r--')
plt.xlabel('Time (hrs)')
plt.ylabel('Height (m)')
plt.legend(['height 1','height 2'])
plt.show()
2. Discretize with Euler's Method
Euler's method is used to solve a set of two differential equations in Excel and Python.
import matplotlib.pyplot as plt
def tank(c1,c2):
Ac = 2 # m^2
qin = 0.5 # m^3/hr
dt = 0.5 # hr
tf = 10.0 # hr
h1 = 0
h2 = 0
t = 0
ts = np.empty(21)
h1s = np.empty(21)
h2s = np.empty(21)
i = 0
while t<=10.0:
ts[i] = t
h1s[i] = h1
h2s[i] = h2
qout1 = c1 * pow(h1,0.5)
qout2 = c2 * pow(h2,0.5)
h1 = (qin-qout1)*dt/Ac + h1
if h1>1:
h1 = 1
h2 = (qout1-qout2)*dt/Ac + h2
i = i + 1
t = t + dt
# plot data
plt.figure(1)
plt.plot(ts,h1s)
plt.plot(ts,h2s)
plt.xlabel("Time (hrs)")
plt.ylabel("Height (m)")
plt.show()
# call function
tank(0.13,0.20)
3. SciPy.Integrate ODEINT Function
See Introduction to ODEINT for more information on solving differential equations with SciPy.
import matplotlib.pyplot as plt
from scipy.integrate import odeint
def tank(h,t):
# constants
c1 = 0.13
c2 = 0.20
Ac = 2 # m^2
# inflow
qin = 0.5 # m^3/hr
# outflow
qout1 = c1 * h[0]**0.5
qout2 = c2 * h[1]**0.5
# differential equations
dhdt1 = (qin - qout1) / Ac
dhdt2 = (qout1 - qout2) / Ac
# overflow conditions
if h[0]>=1 and dhdt1>=0:
dhdt1 = 0
if h[1]>=1 and dhdt2>=0:
dhdt2 = 0
dhdt = [dhdt1,dhdt2]
return dhdt
# integrate the equations
t = np.linspace(0,10) # times to report solution
h0 = [0,0] # initial conditions for height
y = odeint(tank,h0,t) # integrate
# plot results
plt.figure(1)
plt.plot(t,y[:,0],'b-')
plt.plot(t,y[:,1],'r--')
plt.xlabel('Time (hrs)')
plt.ylabel('Height (m)')
plt.legend(['h1','h2'])
plt.show()
APM Python DAE Integrator and Optimizer
This tutorial gives step-by-step instructions on how to simulate dynamic systems. Dynamic systems may have differential and algebraic equations (DAEs) or just differential equations (ODEs) that cause a time evolution of the response. Below is an example of solving a first-order decay with the APM solver in Python. The objective is to fit the differential equation solution to data by adjusting unknown parameters until the model and measured values match.
Scale-up for Large Sets of Equations
Additional Material
This same example problem is also demonstrated with Spreadsheet Programming and in the Matlab programming language. Another example problem demonstrates how to calculate the concentration of CO gas buildup in a room.
