Call Python from MATLAB

There are strengths to both MATLAB and Python. Using MATLAB functions in Python and Python functions in MATLAB are both possible. This tutorial shows how to use Python functions in a MATLAB script. In order to use Python in MATLAB, a Python installation must be available and the Python paths accessible. The easiest way to do this is to install Anaconda and launch MATLAB from the Anaconda prompt.

Exercise 1: Numpy in MATLAB

A first example uses the Numpy (Numerical Python) package in MATLAB to calculate the sine and cosine of values between 0 and 10. The values are computed with Numpy and then returned to MATLAB for plotting.

clear all

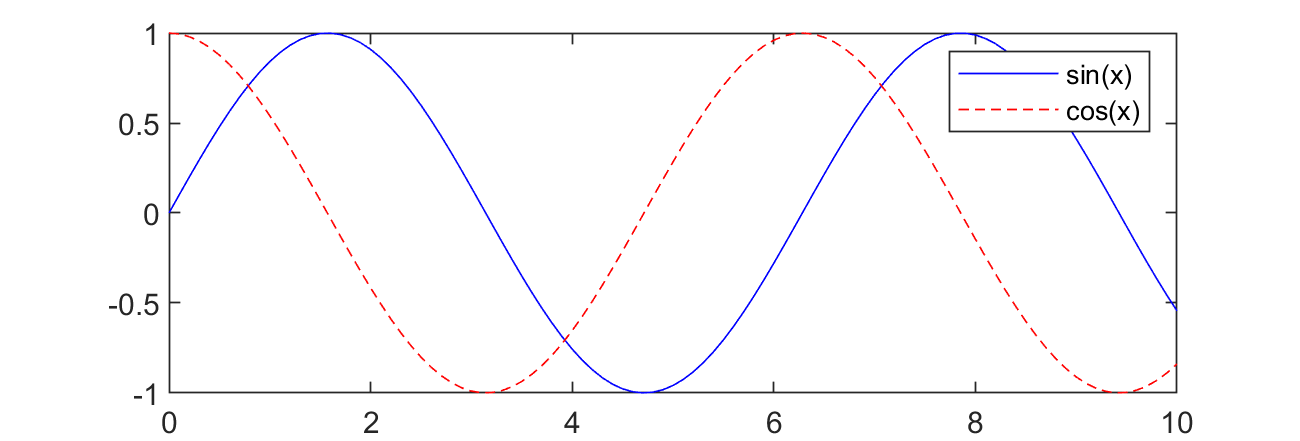
x = py.numpy.linspace(0,10,101);
y = py.numpy.sin(x);
z = py.numpy.cos(x);

xm = cellfun(@double,cell(x.tolist()));
ym = cellfun(@double,cell(y.tolist()));
zm = cellfun(@double,cell(z.tolist()));

plot(xm,ym,'b-')
hold on
plot(xm,zm,'r--')
legend('sin(x)','cos(x)')
[$[Get Code]]

Exercise 2: Gekko Solves Linear Equations in MATLAB

A second example is the solution of two linear equations with Python Gekko in MATLAB.

$$3x+2y=1$$

$$x+2y=0$$

To use the Gekko package in Anaconda (and MATLAB), it must first be installed into the Anaconda package. The easiest way to do this is to open a new Jupyter Notebook session and install with pip package manager. 

  !pip install gekko

If there are not adminstrative privileges, the ---user option can be added to install locally. 

  !pip install --user gekko

MATLAB creates a new Gekko model with m = py.gekko.GEKKO(); and then initializes new variables with statements such as x = m.Var();. Equations are defined with the variables and the double equal sign as m.Equation(3*x+2*y==1);. Finally, the problem is solved with m.solve(); and the results are returned in x.VALUE{1} and y.VALUE{1}.

% start Matlab from Anaconda prompt
close all; clear;
% Solve linear equations
% Initialize Model
m = py.gekko.GEKKO();
% Initialize Variables
x = m.Var();            % define new variable
y = m.Var();            % default=0
% Define Equations
m.Equation(3*x+2*y==1);
m.Equation(x+2*y==0);  
% Solve
m.solve();
% Extract values from Python lists using curly brackets
disp(['x: ' num2str(x.VALUE{1})]);
disp(['y: ' num2str(y.VALUE{1})]);
[$[Get Code]]

Exercise 3: Gekko Solves ODE in MATLAB

A third example is the solution of an ordinary differential equation (ODE) with Python Gekko in MATLAB.

$$k\frac{dy}{dt}==-t y$$

where k is a constant, y is the differential state, and t is time. Similar to the prior problem, MATLAB creates a new Gekko model with m = py.gekko.GEKKO(); and then initializes the y variable with y = m.Var(5.0); with an initial condition of 5. The differential equation is defined with m.Equation(k*y.dt()==-t*y); and IMODE option is changed to dynamic simulation (4). Finally, the problem is solved with m.solve(); and the results are returned in y.VALUE.value.

% start Matlab from Anaconda prompt
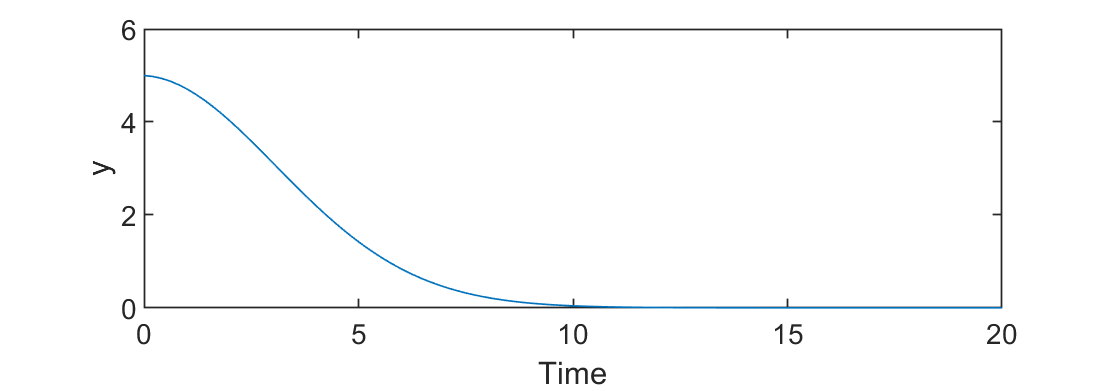
close all; clear;

% Solve differential equation
m = py.gekko.GEKKO(pyargs('remote','False'));  % Solve on local machine
m.time = py.numpy.linspace(0,20,100);
k = 10;
y = m.Var(5.0);
t = m.Param(m.time);
m.Equation(k*y.dt()==-t*y);
m.options.IMODE = 4;
m.solve()

% retrieving the values is a little more complicated here
time = cellfun(@double,cell(m.time.tolist()));
y = cellfun(@double,cell(y.VALUE.value));
plot(time,y)
xlabel('Time')
ylabel('y')
[$[Get Code]]

Thanks to Abe Martin for generating the examples.

💬