Piece-wise Function with Lookup Object

(:source lang=python:)

(:sourceend:)

(:source lang=python:)

(:sourceend:)

(:source lang=python:)

(:sourceend:)

PWL in GEKKO Python

(:source lang=python:) from scipy import optimize import matplotlib.pyplot as plt from gekko import GEKKO import numpy as np

m = GEKKO() m.options.SOLVER = 1

xz = m.FV(value = 4.5) yz = m.Var()

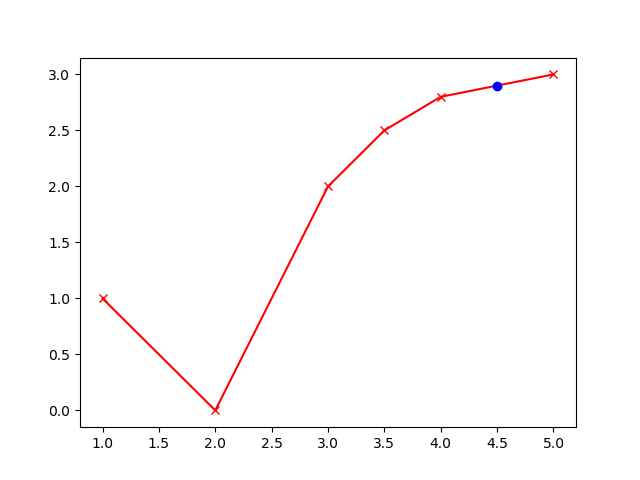
xp_val = np.array([1, 2, 3, 3.5, 4, 5]) yp_val = np.array([1, 0, 2, 2.5, 2.8, 3]) xp = [m.Param(value=xp_val[i]) for i in range(6)] yp = [m.Param(value=yp_val[i]) for i in range(6)]

x = [m.Var(lb=xp[i],ub=xp[i+1]) for i in range(5)] x[0].lower = -1e20 x[-1].upper = 1e20

1. Variables

slk_u = [m.Var(value=1,lb=0) for i in range(4)] slk_l = [m.Var(value=1,lb=0) for i in range(4)]

1. Intermediates

slope = [] for i in range(5):

    slope.append(m.Intermediate((yp[i+1]-yp[i]) / (xp[i+1]-xp[i])))

y = [] for i in range(5):

    y.append(m.Intermediate((x[i]-xp[i])*slope[i]))

for i in range(4):

    m.Obj(slk_u[i] + slk_l[i])

m.Equation(xz == x[0] + slk_u[0]) for i in range(3):

    m.Equation(xz == x[i+1] + slk_u[i+1] - slk_l[i])

m.Equation(xz == x[4] - slk_l[3])

m.Equation(yz == yp[0] + y[0] + y[1] + y[2] + y[3] + y[4])

m.solve()

plt.plot(xp,yp,'rx-',label='PWL function') plt.plot(xz,yz,'bo',label='Data') plt.show() (:sourceend:)

APMonitor PWL Object

  File p.txt
    1,   1
    2,   0
    3,   2
    3.5, 2.5
    4,   2.8
    5,   3
  End File

  Objects
    p = pwl
  End Objects

  Connections
    x = p.x
    y = p.y
  End Connections

</pre></font> (:htmlend:)

Equivalent Problem with Slack Variables

(:html:)<font size=2><pre>

  Parameters
    ! independent variable
    x = 6.0

    ! data points
    xp[1] = 1
    yp[1] = 1

    xp[2] = 2
    yp[2] = 0

    xp[3] = 3
    yp[3] = 2

    xp[4] = 3.5
    yp[4] = 2.5

    xp[5] = 4
    yp[5] = 2.8

    xp[6] = 5
    yp[6] = 3
  End Parameters

  Variables
    ! piece-wise linear segments
    x[1]             <=xp[2]
    x[2:4] >xp[2:4], <=xp[3:5]
    x[5]   >xp[5]

    ! dependent variable
    y

    ! slack variables
    slk_u[1:4]
    slk_l[2:5]
  End Variables

In Situ Adaptive Tabulation (ISAT) is an example of a multi-dimensional piecewise linear approximation. The piecewise linear segments are built dynamically as new data becomes available. This way, only regions that are accessed in practice contribute to the function approximation.

    minimize slk_u[1:4]
    minimize slk_l[2:5]

File m.csv

  End Equations

End Model </pre></font> (:htmlend:)

(:html:)<font size=2><pre>

Piece-wise function with the LOOKUP object

create the csv file

File *.m.csv

  input,  y[1],  y[2]
      1,     2,    4
      3,     4,    6
      5,    -5,   -7
     -1,     1,  0.5

End File

define lookup object m

Objects

  m = lookup

End Objects

connect m properties with model parameters

Connections

  x = m.input
  y[1] = m.y[1]
  y[2] = m.y[2]

End Connections

simple model

Model n

  Parameters
    x = 1
    y[1]
    y[2]
  End Parameters

  Variables
    y
  End Variables

  Equations
    y = y[1]+y[2]

(:html:)<font size=2><pre>

(:htmlend:)

(:html:)<font size=1><pre> Model pwl

  Parameters
    ! independent variable
    x = 6.0

    ! data points
    xp[1] = 1
    yp[1] = 1

    xp[2] = 2
    yp[2] = 0

    xp[3] = 3
    yp[3] = 2

    xp[4] = 3.5
    yp[4] = 2.5

    xp[5] = 4
    yp[5] = 2.8

    xp[6] = 5
    yp[6] = 3
  End Parameters

  Variables
    ! piece-wise linear segments
    x[1]             <=xp[2]
    x[2:4] >xp[2:4], <=xp[3:5]
    x[5]   >xp[5]

    ! dependent variable
    y

    ! slack variables
    slk_u[1:4]
    slk_l[2:5]
  End Variables

  Intermediates
    slope[1:5] = (yp[2:6]-yp[1:5]) / (xp[2:6]-xp[1:5])
    y[1:5] = (x[1:5]-xp[1:5])*slope[1:5]
  End Intermediates

  Equations
    x = x[1]   + slk_u[1]
    x = x[2:4] + slk_u[2:4] - slk_l[2:4]
    x = x[5]                - slk_l[5]

    y = yp[1] + y[1] + y[2] + y[3] + y[4] + y[5]
  End Equations

End Model </pre></font> (:htmlend:)

Piece-wise Linear Approximation

• Piece-wise Linear Approximation Example

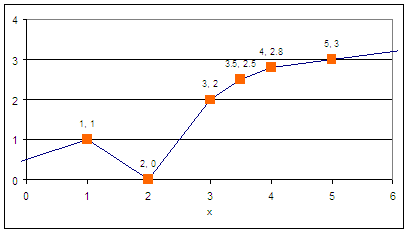
A piece-wise linear function is an approximation of a nonlinear relationship. For more nonlinear relationships, additional linear segments are added to refine the approximation.

As an example, the piecewise linear form is often used to approximate valve characterization (valve position (% open) to flow). This is a single input-single output function approximation.

In Situ Adaptive Tabulation (ISAT) is an example of a multi-dimensional piecewise linear approximation. The piecewise linear segments are built dynamically as new data becomes available. This way, only regions that are accessed in practice contribute to the function approximation.