Python Optimization Package
 APM Python is designed for large-scale optimization and accesses solvers of constrained, unconstrained, continuous, and discrete problems. Problems in linear programming, quadratic programming, integer programming, nonlinear optimization, systems of dynamic nonlinear equations, and multiobjective optimization can be solved. The platform can find optimal solutions, perform tradeoff analyses, balance multiple design alternatives, and incorporate optimization methods into external modeling and analysis software. It is free for academic and commercial use.
APM Python is designed for large-scale optimization and accesses solvers of constrained, unconstrained, continuous, and discrete problems. Problems in linear programming, quadratic programming, integer programming, nonlinear optimization, systems of dynamic nonlinear equations, and multiobjective optimization can be solved. The platform can find optimal solutions, perform tradeoff analyses, balance multiple design alternatives, and incorporate optimization methods into external modeling and analysis software. It is free for academic and commercial use.Recommended: A newer Python interface is the GEKKO Optimization Suite that is available with:
python pip install gekko
Instructions below are for working with the original APM Python package that requires an APM model and data files. The advantage of working with GEKKO is that the model equations and data are defined directly within the Python language instead of in separate files (see documentation). There is also an option to run locally in GEKKO without an Apache server for Linux and Windows. Both APM Python and GEKKO solve optimization problems on public servers by default and this option is available for all platforms (Windows, Linux, MacOS, ARM processors, etc) that run Python.
Example applications of nonlinear models with differential and algebraic equations are available for download below or from the following GitHub repository.
git clone git://github.com/APMonitor/apm_python
The APMonitor package is also available through the package manager pip in Python.
python pip install APMonitor
Another method to obtain APMonitor is to include the following code snippet at the beginning of a Python script. The installation is only required once and then the code can be commented or removed.
from pip import main as pipmain
except:
from pip._internal import main as pipmain
pipmain(['install','APMonitor'])
# to upgrade: pipmain(['install','--upgrade','APMonitor'])
Download APM Python Library and Example Problems
The latest APM Python libraries are attached below. Functionality has been tested with Python 2.7 and 3.5. Example applications that use the apm.py library are listed further down on this page.
 Download APM Python (version 0.7.6) - Released 31 Jan 2017
Download APM Python (version 0.7.6) - Released 31 Jan 2017The development roadmap for this and other libraries are detailed in the release notes. The zipped archive contains the APM Python library apm.py and a number of example problems in separate folders. Descriptions of some of the example problems are provided below.
Example_hs071: Nonlinear Programming with Python
$$ \min x_1 x_4 (x_1 + x_2 + x_3) + x_3 $$
$$ \mathrm{subject\;to} \quad x_1 x_2 x_3 x_4 \ge 25$$
$$\quad x_1^2 + x_2^2 + x_3^2 + x_4^2 = 40$$
$$\quad 1 \le x_1, x_2, x_3, x_4 \le 5$$
$$\quad x_0 = (1,5,5,1)$$
- Solve this optimization problem from a web-browser interface or download the Python source above. The Python files are contained in folder example_hs71.
Example_nlc: Nonlinear Control with Python
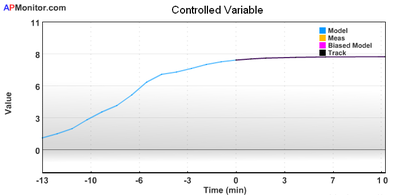
Example_tank_mhe/nlc: Nonlinear Estimation and Control with Python
In this case study, a gravity drained tank was operated to generate data. A dynamic model of the process was derived from a material balance. This material balance is displayed below, along with a diagram of the system.

The the unknown parameters c1 and c2 need to be determined. The parameter c1 is the flow into the tank when the valve is fully open. The parameter c2 is the relationship between the volume of water in the tank and the outlet flow. This model is nonlinear because the outlet flow depends on the square root of the liquid volume. Nonlinear estimation is a technique to determine parameters based on the measurements. The script in example_tank_mhe uses the process data and the nonlinear model to determine the optimal parameters c1 and c2.
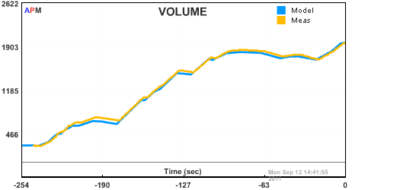
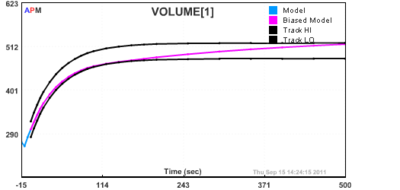
After an accurate model of the process is obtained, the model can be used in a Nonlinear Control (NLC) application. A PID controller is compared to the NLC response in the folder example_tank_nlc.
Other Applications with Python
- APM IPython Notebook Example on GitHub
- Diabetic Blood Glucose Control
- Distillation Column
- Stirred Reactor
The Dynamic Optimization Course is graduate level course taught over 14 weeks to introduce concepts in mathematical modeling, data reconciliation, estimation, and control. There are many other applications and instructional material posted to this freely available course web-site.