Simulation of Infectious Disease Spread

Measles (sometimes known as English Measles) is spread through respiration (contact with fluids from an infected person's nose and mouth, either directly or through aerosol transmission), and is highly contagious—90% of people without immunity sharing living space with an infected person will catch it. The infection has an average incubation period of 14 days (range 6–19 days) and infectivity lasts from 2–4 days prior, until 2–5 days following the onset of the rash (i.e. 4–9 days infectivity in total).

Understanding the spread of the measles virus from historical data of major metropolitan areas will help researchers understand the fundamentals of disease spread through a population. This may help guide policy for school closure, travel restrictions, and other measures intended to slow disease spread until a vaccine can be developed or deployed.

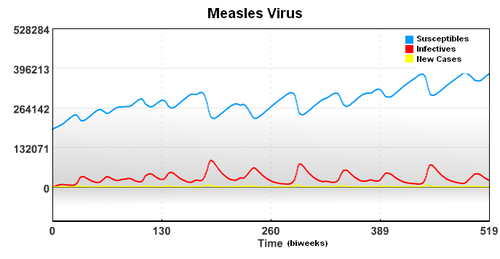
In this case, the starting population of 3,200,000 is composed of a group of Susceptible, Infected, and Recovered individuals. To account for underreporting of measles cases, a reporting factor is used in the model. In this study, it is assumed that only 45% of the measles cases were reported.

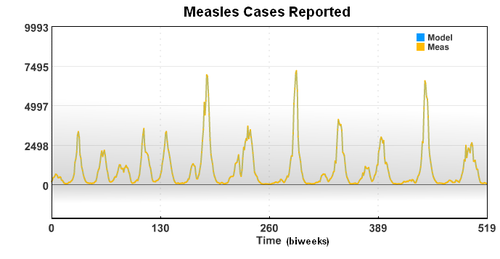
The new case data shows a seasonal variation that is caused by an increased rate of contact between the susceptible population and the infective population. Based on the new case data (cases), birth rate (mu), and recovery rate (gamma), the seasonal variation of the transmission parameter is estimated over a period of 20 years.

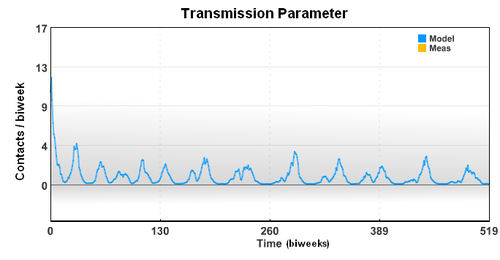
The seasonal transmission parameter can also be used to estimate spread of other diseases. The transmission parameter is the number of contact (on average) made with other individuals during a biweek period. The transmission parameter can sometimes be decreased for brief periods of time to slow the spread of a disease. Also, the number of susceptible individuals can be reduced through the use of vaccines. In the case of limited vaccine supply, disease spread models can help identify the best use the resources to limit large outbreaks.

Infectious Disease Estimation in MATLAB and Python
! APMonitor Modeling Language
!
! Data from New York for the years 1947-1965
! Data from Bangkok for the years 1975-1984
! Data from London is 1944-1966?
!
Model disease
  Parameters
    ! population size        (individuals)
    N           = 3.2e6              
    ! birth rate             (births/biweek/total population)
    mu          = 7.8e-4            
    ! recovery rate          (recoveries/biweek/infectives)
    gamma       = 0.07              
    ! reporting fraction to account for underreporting                
    rep_frac    = 0.45
    ! cases reported         (new individuals infected per biweek)
    cases = 180, >= 0                
  End Parameters

  Variables
    ! transmission parameter (potentially infectious contacts/biweek)
    beta = 10
    ! susceptibles           (individuals in the total population)
    S = 0.06*N, >= 0, <= N
    ! infectives             (individuals infected)
    I = 0.0001*N, >= 0, <= N
  End Variables

  Intermediates
    ! infection rate per biweek
    R = beta * S * I / N
  End Intermediates

  Equations
    $S = -R +  mu * N
    $I =  R -  gamma * I
    cases = rep_frac * R
  End Equations
End Model
[$[Get Code]]
Control Measles Outbreak with Optimal Vaccination Scheduling

Solution (Python GEKKO)

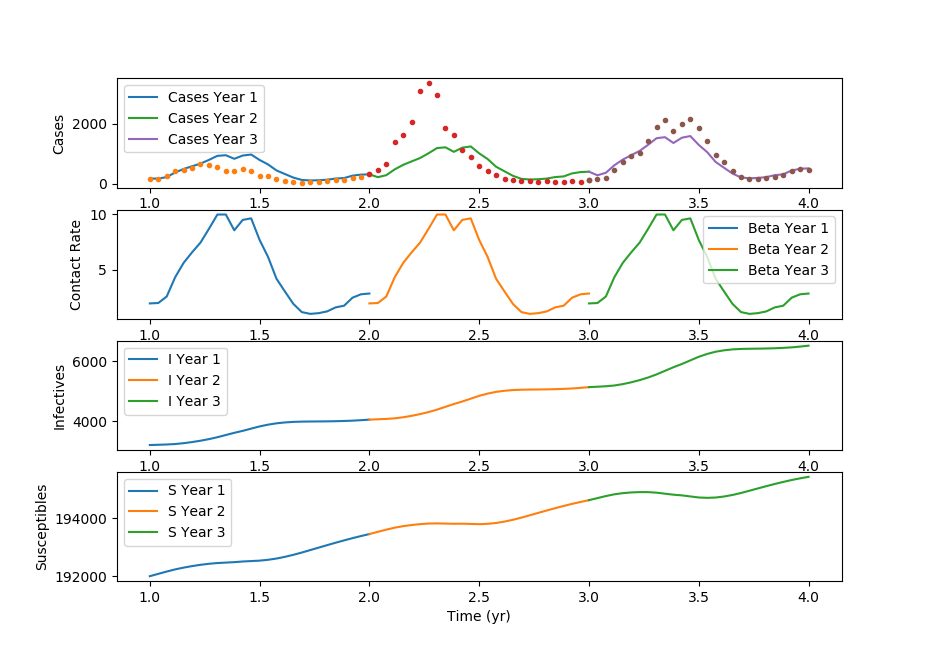
Thanks to Cameron Price for providing the GEKKO Python code.

Estimate 26 beta values and gamma

import numpy as np
from gekko import GEKKO
import matplotlib.pyplot as plt

# Import Data
# write csv data file
t_s = np.linspace(0,78,79)
# case data
cases_s = np.array([180,180,271,423,465,523,649,624,556,420,\
                  423,488,441,268,260,163,83,60,41,48,65,82,\
                  145,122,194,237,318,450,671,1387,1617,2058,\
                  3099,3340,2965,1873,1641,1122,884,591,427,282,\
                  174,127,84,97,68,88,79,58,85,75,121,174,209,458,\
                  742,929,1027,1411,1885,2110,1764,2001,2154,1843,\
                  1427,970,726,416,218,160,160,188,224,298,436,482,468])

# Initialize gekko model
m = GEKKO()

# Number of collocation nodes
nodes = 4

# Number of phases (years in this case)
n = 3

#Biweek periods per year
bi = 26

# Time horizon (for all 3 phases)
m.time = np.linspace(0,1,bi+1)

# Parameters that will repeat each year
N        = m.Param(3.2e6)
mu       = m.Param(7.8e-4)
rep_frac = m.Param(0.45)
Vr       = m.Param(0)

beta     = m.MV(2,lb = 0.1)
beta.STATUS = 1

gamma = m.FV(value=0.07)
gamma.STATUS = 1
gamma.LOWER = 0.05
gamma.UPPER = 0.5

# Data used to control objective function
casesobj1 = m.Param(cases_s[0:(bi+1)])
casesobj2 = m.Param(cases_s[bi:(2*bi+1)])
casesobj3 = m.Param(cases_s[2*bi:(3*bi+1)])

# Variables that vary between years, one version for each year
cases = [m.CV(value = cases_s[(i*bi):(i+1)*(bi+1)-i],lb=0) for i in range(n)]
for i in cases:
    i.FSTATUS = 1
    i.WMODEL = 0
    i.MEAS_GAP = 100

S = [m.Var(0.06*N,lb = 0,ub = N) for i in range(n)]
I = [m.Var(0.001*N, lb = 0,ub = N) for i in range(n)]
V = [m.Var(2e5) for i in range(n)]

# Equations (created for each year)
for i in range(n):
    R = m.Intermediate(beta*S[i]*I[i]/N)
    m.Equation(S[i].dt() == -R + mu*N - Vr)
    m.Equation(I[i].dt() == R - gamma*I[i])
    m.Equation(cases[i] == rep_frac*R)
    m.Equation(V[i].dt() == -Vr)

# Connect years together at endpoints
for i in range(n-1):
    m.Connection(cases[i+1],cases[i],1,bi,1,nodes)#,1,nodes)
    m.Connection(cases[i+1],'CALCULATED',pos1=1,node1=1)
    m.Connection(S[i+1],S[i],1,bi,1,nodes)
    m.Connection(S[i+1],'CALCULATED',pos1=1,node1=1)
    m.Connection(I[i+1],I[i],1,bi,1,nodes)
    m.Connection(I[i+1],'CALCULATED',pos1=1, node1=1)

# Solver options
m.options.IMODE = 5
m.options.NODES = nodes
m.EV_TYPE = 1
m.options.SOLVER = 1

# Solve
m.Obj(2*(casesobj1-cases[0])**2+(casesobj3-cases[2])**2)

m.solve()

# Calculate the start time of each phase
ts = np.linspace(1,n,n)

# Plot
plt.figure()
plt.subplot(4,1,1)
tm = np.empty(len(m.time))
for i in range(n):
    tm = m.time + ts[i]
    plt.plot(tm,cases[i].value,label='Cases Year %s'%(i+1))
    plt.plot(tm,cases_s[(i*bi):(i+1)*(bi+1)-i],'.')
plt.legend()
plt.ylabel('Cases')

plt.subplot(4,1,2)
for i in range(n):
    tm = m.time + ts[i]
    plt.plot(tm,beta.value,label='Beta Year %s'%(i+1))
plt.legend()
plt.ylabel('Contact Rate')

plt.subplot(4,1,3)
for i in range(n):
    tm = m.time + ts[i]
    plt.plot(tm,I[i].value,label='I Year %s'%(i+1))
plt.legend()
plt.ylabel('Infectives')

plt.subplot(4,1,4)
for i in range(n):
    tm = m.time + ts[i]
    plt.plot(tm,S[i].value,label='S Year %s'%(i+1))
plt.legend()
plt.ylabel('Susceptibles')
plt.xlabel('Time (yr)')

plt.show()
[$[Get Code]]

See also: Optimal measles vaccine distribution

References

  • Daniel P. Word, George H. Abbott, Derek Cummings, and Carl D. Laird, "Estimating Seasonal Drivers in Childhood Infectious Diseases with Continuous Time and Discrete-Time Models", in Proceedings, 2010 American Control Conference, pp. 5137-5142, Baltimore, MD, June 29 - July 2, 2010.
  • Daniel P. Word, James K. Young, Derek Cummings, Carl D. Laird, "Estimation of seasonal transmission parameters in childhood infectious disease using a stochastic continuous time model", Computer Aided Chemical Engineering, pp. 229-234, 28, 2010.
💬