• (:html:)<a href="/online/plot.php?d=oscillator&f=SV(2).xml">Signal</a>(:htmlend:)
• (:html:)<a href="/online/plot.php?d=oscillator&f=SV(3).xml">Signal Derivative</a>(:htmlend:)

(:html:)<font size=2><pre>

(:htmlend:)

(:html:)<font size=1><pre>

APMonitor Modeling Language

https://www.apmonitor.com

Model osc

  Parameters
    mu = 1
    A = 1
    omega = 2
    b = 2
  End Parameters

  Variables
    t = 0
    x = b
    y = b/(mu*(1-b^2))
  End Variables

  Equations
    ! time integrator
    $t = 1

    ! oscillator
    $x = y
    $y + mu*(x^2-1)*$x + x = A * sin(omega*t)
  End Equations

End Model </pre></font> (:htmlend:)

The van der Pol oscillator was originally discovered by the Dutch electrical engineer and physicist Balthasar van der Pol. Van der Pol found stable oscillations, now known as limit cycles, in electrical circuits employing vacuum tubes. When these circuits are driven near the limit cycle they become entrained, i.e. the driving signal pulls the current along with it. Van der Pol and his colleague van der Mark reported in that at certain drive frequencies an irregular noise was heard. This irregular noise was always heard near the natural entrainment frequencies. This was one of the first discovered instances of deterministic chaos.

• (:html:)<a href="https://apmonitor.ath.cx/online/plot.php?d=oscillator&f=SV(3).xml">Signal Derivative</a>(:htmlend:)

Van der Pol oscillator

The Van der Pol oscillator (named for Dutch physicist Balthasar van der Pol) is a type of nonconservative oscillator with nonlinear damping. It evolves in time according to the second order differential equation:

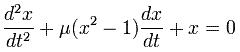
The van der Pol oscillator was originally discovered by the Dutch electrical engineer and physicist Balthasar van der Pol. Van der Pol found stable oscillations, now known as limit cycles, in electrical circuits employing vacuum tubes. When these circuits are driven near the limit cycle they become entrained, i.e. the driving signal pulls the current along with it. Van der Pol and his colleague van der Mark reported in the September 1927 issue of Nature that at certain drive frequencies an irregular noise was heard. This irregular noise was always heard near the natural entrainment frequencies. This was one of the first discovered instances of deterministic chaos.

Model

• oscillator.apm

Sample Results

Input

The oscillator is driven with a sine wave forcing function at 60 Hz and amplitude 1.

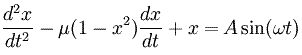
Predictions

• (:html:)<a href="https://apmonitor.ath.cx/online/plot.php?d=oscillator&f=SV(2).xml">Signal</a>(:htmlend:)
• (:html:)<a href="https://apmonitor.ath.cx/online/plot.php?d=cells&f=SV(3).xml">Signal Derivative</a>(:htmlend:)