Distillation Column
Binary Distillation Column
This distillation column is a separation of cyclohexane and n-heptane. The two components are separated over 30 theoretical trays. In general, distillation column models are generally good test cases for nonlinear model reduction and identification. The concentrations at each stage or tray are highly correlated. The dynamics of the distillation process can be described by a relatively few number of underlying dynamic states.
This model was published in:
Hahn, J. and T.F. Edgar, An improved method for nonlinear model reduction using balancing of empirical gramians, Computers and Chemical Engineering, 26, pp. 1379-1397, (2002)
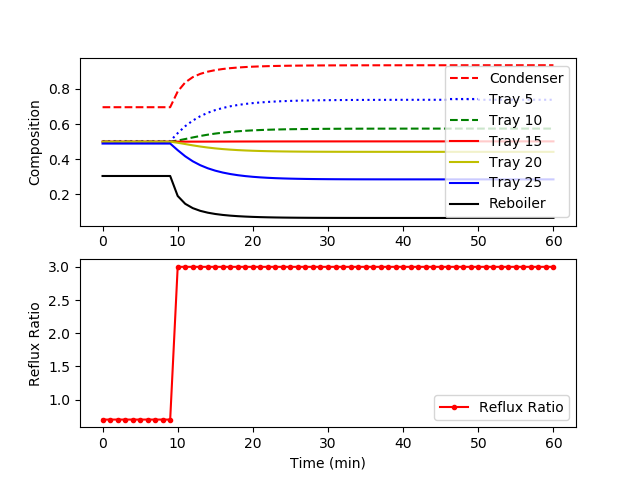
The model is available as a Python script with solution provided by GEKKO. The following figure shows a step change in the reflux ratio from 0.7 to 3.0.
import numpy as np
import matplotlib.pyplot as plt
# Initialize Model
m = GEKKO()
# Define constants
#Reflux Ratio
rr=m.Param(value=0.7)
# Feed flowrate (mol/min)
Feed=m.Const(value=2)
# Mole fraction of feed
x_Feed=m.Const(value=.5)
#Relative volatility = (yA/xA)/(yB/xB) = KA/KB = alpha(A,B)
vol=m.Const(value=1.6)
# Total molar holdup on each tray
atray=m.Const(value=.25)
# Total molar holdup in condenser
acond=m.Const(value=.5)
# Total molar holdup in reboiler
areb=m.Const(value=.1)
# mole fraction of component A
x=[]
for i in range(32):
x.append(m.Var(.3))
# Define intermediates
# Distillate flowrate (mol/min)
D=m.Intermediate(.5*Feed)
# Liquid flowrate in rectification section (mol/min)
L=m.Intermediate(rr*D)
# Vapor Flowrate in column (mol/min)
V=m.Intermediate(L+D)
# Liquid flowrate in stripping section (mol/min)
FL=m.Intermediate(Feed+L)
# vapor mole fraction of Component A
# From the equilibrium assumption and mole balances
# 1) vol = (yA/xA) / (yB/xB)
# 2) xA + xB = 1
# 3) yA + yB = 1
y=[]
for i in range(32):
y.append(m.Intermediate(x[i]*vol/(1+(vol-1)*x[i])))
# condenser
m.Equation(acond*x[0].dt()==V*(y[1]-x[0]))
# 15 column stages
n=1
for i in range(15):
m.Equation(atray * x[n].dt() ==L*(x[n-1]-x[n]) - V*(y[n]-y[n+1]))
n=n+1
# feed tray
m.Equation(atray * x[16].dt() == Feed*x_Feed + L*x[15] - FL*x[16] - V*(y[16]-y[17]))
# 14 column stages
n=17
for i in range(14):
m.Equation(atray * x[n].dt() == FL*(x[n-1]-x[n]) - V*(y[n]-y[n+1]))
n=n+1
# reboiler
m.Equation(areb * x[31].dt() == FL*x[30] - (Feed-D)*x[31] - V*y[31])
# steady state solution
m.solve()
print(x) # with RR=0.7
# switch to dynamic simulation
m.options.imode=4
nt = 61
m.time=np.linspace(0,60,61)
# step change in reflux ratio
rr_step = np.ones(nt) * 0.7
rr_step[10:] = 3.0
rr.value=rr_step
m.solve()
plt.subplot(2,1,1)
plt.plot(m.time,x[0].value,'r--',label='Condenser')
plt.plot(m.time,x[5].value,'b:',label='Tray 5')
plt.plot(m.time,x[10].value,'g--',label='Tray 10')
plt.plot(m.time,x[15].value,'r-',label='Tray 15')
plt.plot(m.time,x[20].value,'y-',label='Tray 20')
plt.plot(m.time,x[25].value,'b-',label='Tray 25')
plt.plot(m.time,x[31].value,'k-',label='Reboiler')
plt.ylabel('Composition')
plt.legend(loc='best')
plt.subplot(2,1,2)
plt.plot(m.time,rr.value,'r.-',label='Reflux Ratio')
plt.ylabel('Reflux Ratio')
plt.legend(loc='best')
plt.xlabel('Time (min)')
plt.show()
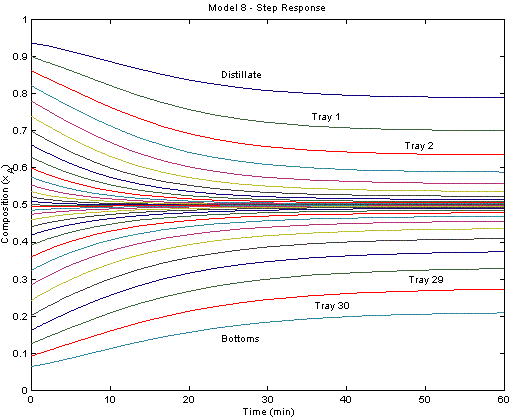
The model is also available in the APMonitor Modeling Language. The figure below displays the system response after a step change in the reflux ratio from 3.0 to 1.5. Each trajectory represents the mole fraction of cyclohexane at each tray. The top reflux material becomes less pure (more n-heptane) due to the increased draw from the top of the column.
! https://www.apmonitor.com
! Binary Distillation Column from
!
! Hahn, J. and T.F. Edgar, An improved method for
! nonlinear model reduction using balancing of
! empirical gramians, Computers and Chemical
! Engineering, 26, pp. 1379-1397, (2002)
!
! Liquid mole fraction of component A
! at reflux ratio = 2
!
! Condenser 0.93541941614016
! Tray 1 0.90052553715795
! Tray 2 0.86229645132283
! . 0.82169940277993
! . 0.77999079584355
! . 0.73857168629759
! . 0.69880490932694
! . 0.66184253445732
! . 0.62850777645505
! . 0.59925269993058
! . 0.57418567956453
! . 0.55314422743545
! . 0.53578454439850
! . 0.52166550959767
! . 0.51031495114413
! . 0.50127509227528
! . 0.49412891686784
! . 0.48544992019184
! . 0.47420248108803
! . 0.45980349896163
! . 0.44164297270225
! . 0.41919109776836
! . 0.39205549194059
! . 0.36024592617390
! . 0.32407993023343
! . 0.28467681591738
! . 0.24320921343484
! . 0.20181568276528
! . 0.16177269003094
! Tray 29 0.12514970961746
! Tray 30 0.09245832612765
! Reboiler 0.06458317697321
Model binary
Parameters
! reflux ratio
rr = 0.7
! Feed Flowrate (mol/min)
Feed = 2.0 ! 24.0/60.0
! Mole Fraction of Feed
x_Feed = 0.5
! Relative Volatility = (yA/xA)/(yB/xB) = KA/KB = alpha(A,B)
vol=1.6
! Total Molar Holdup in the Condenser
atray=0.25
! Total Molar Holdup on each Tray
acond=0.5
! Total Molar Holdup in the Reboiler
areb=0.1
End Parameters
Variables
! mole fraction of component A
x[1:32] = 0.3
End Variables
Intermediates
! Distillate Flowrate (mol/min)
D=0.5*Feed
! Flowrate of the Liquid in the Rectification Section (mol/min)
L=rr*D
! Vapor Flowrate in the Column (mol/min)
V=L+D
! Flowrate of the Liquid in the Stripping Section (mol/min)
FL=Feed+L
! Vapor Mole Fractions of Component A
! From the equilibrium assumption and mole balances
! 1) vol = (yA/xA) / (yB/xB)
! 2) xA + xB = 1
! 3) yA + yB = 1
y[1:32] = x[1:32]*vol/(1+(vol-1)*x[1:32])
End Intermediates
Equations
! condenser
acond * $x[1] = V*(y[2]-x[1])
! 15 column stages
atray * $x[2:16] = L*(x[1:15]-x[2:16]) - V*(y[2:16]-y[3:17])
! feed tray
atray * $x[17] = Feed*x_Feed + L*x[16] - FL*x[17] - V*(y[17]-y[18])
! 14 column stages
atray * $x[18:31] = FL*(x[17:30]-x[18:31]) - V*(y[18:31]-y[19:32])
! reboiler
areb * $x[32] = FL*x[31] - (Feed-D)*x[32] - V*y[32]
End Equations
End Model
Multi-component Distillation Column
The distillation column in this example is built from a number of pre-existing model objects. The model objects used in this example include the distillation stage, feed, flash, mixer, splitter, stream lag, and vessel. These basic models are connected to form the multicomponent distillation tower.