Aircraft Optimization
The aircraft optimization problem is based on a simple aircraft model. The mathematical equations are ordinary differential equations (ODEs) that are integrated to final time T. The objective is to minimize the time required to achieve zero angle of attack, pitch angle, and pitch rate. The manipulated variable (control) is the aileron angle.
$$ \begin{array}{llcl} \min_{x, w, T} & T \\ \mbox{s.t.} & \dot{x}_0 &=& -0.877 \; x_0 + x_2 - 0.088 \; x_0 \; x_2 + 0.47 \; x_0^2 \\ &&& - 0.019 \; x_1^2 - x_0^2 \; x_2 + 3.846 \; x_0^3 \\ &&& - 0.215 \; w + 0.28 \; x_0^2 \; w + 0.47 \; x_0 \; w^2 + 0.63 \; w^3 \\ & \dot{x}_1 &=& x_2 \\ & \dot{x}_2 &=& -4.208 \; x_0 - 0.396 \; x_2 - 0.47 \; x_0^2 - 3.564 \; x_0^3 \\ &&& -20.967 \; w + 6.265 \; x_0^2 \; w + 46 \; x_0 \; w^2 + 61.4 \; w^3 \\ & x(0) &=& (0.4655,0,0)^T \\ & x(T) &=& (0,0,0)^T \\ & w(t) &\in& \{-0.05236,0.05236\} \end{array} $$
where `x_0` is the angle of attack in radians, `x_1` is the pitch angle, `x_2` is the pitch rate in rad/s, and the control function `w` is the tail deflection angle in radians. Both initial and terminal values of the differential states are fixed.
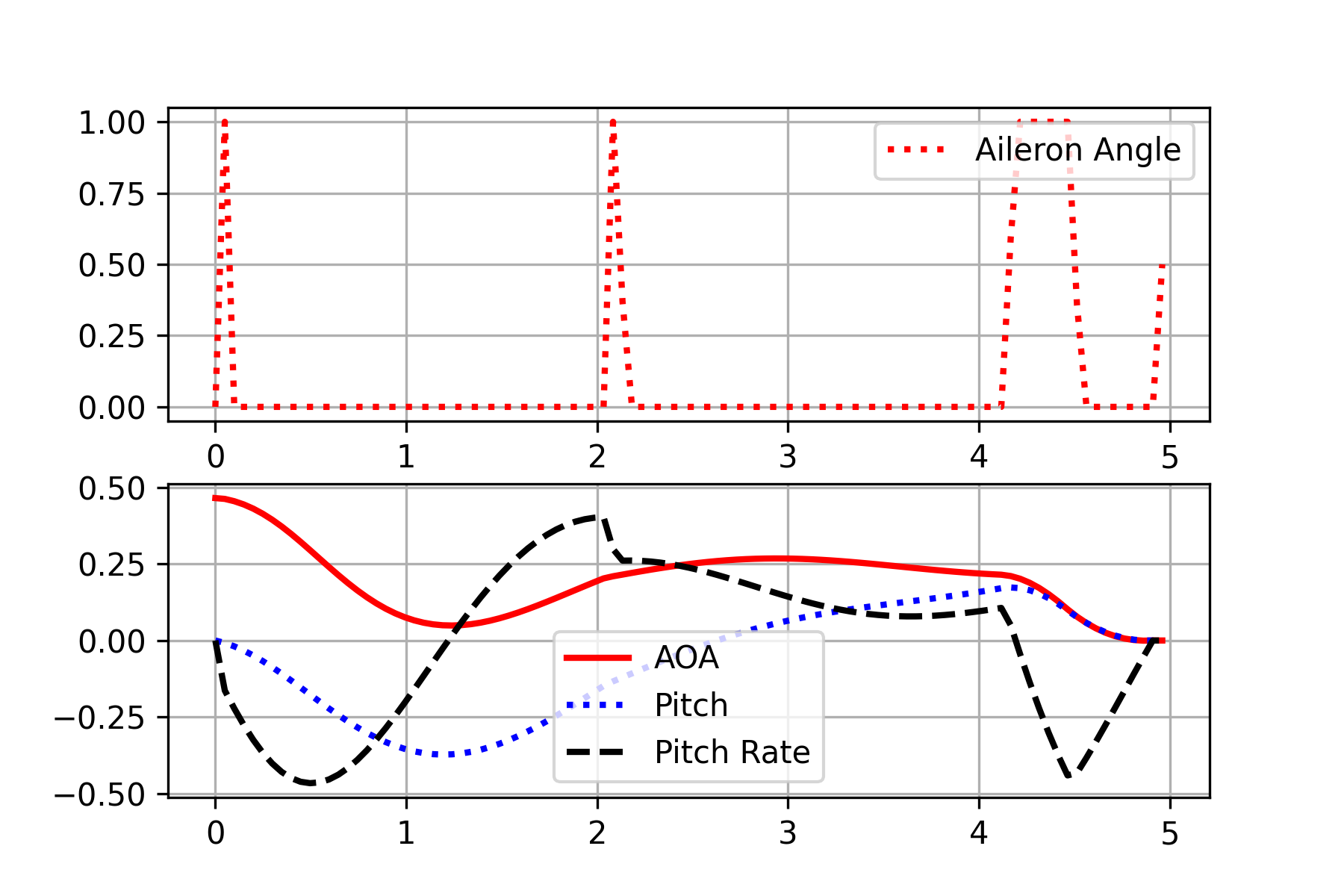
The problem is transformed to aileron angle 0 to 1 with an equivalent substitution.
import numpy as np
import matplotlib.pyplot as plt
m = GEKKO(remote=False)
n = 101; m.time = np.linspace(0,1,n)
ksi = 0.05236
tf = m.FV(value=5, lb=1, ub=10)
tf.STATUS = 1
m.Minimize(tf/n)
# x0 = angle of attack
# x1 = pitch angle
# x2 = pitch rate
x0,x1,x2 = m.Array(m.Var,3,value=0,lb=-1,ub=1)
x0.value = 0.4655
# Control signal - aileron angle
w = m.MV(value=0, lb=0, ub=1); w.STATUS=1
m.Equation(x0.dt()/tf == -0.877*x0 + x2 - 0.088*x0*x2
+ 0.47*x0**2 - 0.019*x1**2 -x0**2*x2 + 3.846*x0**3
-(0.215*ksi-0.28*x0**2*ksi -0.47*x0*ksi**2 - 0.63*ksi**3)*w
-(-0.215*ksi + 0.28*x0**2 -0.47*x0*ksi**2 + 0.63*ksi**3)*(1-w))
m.Equation(x1.dt()/tf==x2)
m.Equation(x2.dt()/tf == -4.208*x0 - 0.396*x2 - 0.47*x0**2 - 3.564*x0**3
+20.967*ksi - 6.265*x0**2*ksi + 46*x0*ksi**2 -61.4*ksi**3
-(20.967*ksi - 6.265*x0**2*ksi - 61.4*ksi**3)*2*w)
m.fix_final(x0,0)
m.fix_final(x1,0)
m.fix_final(x2,0)
m.options.IMODE=6
m.options.SOLVER=1
m.options.MAX_ITER=1000
m.options.COLDSTART=0
m.solve()
tm = tf.value[0]*m.time
plt.figure(figsize=(6,4))
plt.subplot(2,1,1)
plt.plot(tm,w,'r:',lw=2,label='Aileron Angle')
plt.grid(); plt.legend()
plt.subplot(2,1,2)
plt.plot(tm,x0,'r-',lw=2,label='AOA')
plt.plot(tm,x1,'b:',lw=2,label='Pitch')
plt.plot(tm,x2,'k--',lw=2,label='Pitch Rate')
plt.grid(); plt.legend()
plt.savefig('aircraft.png',dpi=300);
plt.tight_layout(); plt.show()

The Gekko Optimization Suite is a machine learning and optimization package in Python for mixed-integer and differential algebraic equations.
📄 Gekko Publication and References
The GEKKO package is available in Python with pip install gekko. There are additional example problems for equation solving, optimization, regression, dynamic simulation, model predictive control, and machine learning.