Lecture 6 - Fitting models to data

The Gain (K_p), Time Constant (tau_p), and Dead-time (theta_p) can be graphically extracted from a step test when fitting to a First Order Plus Dead Time (FOPDT) model. There are many situations when it is not possible or doesn't make sense to generate a complete step test or there are other model forms that better describe the system.

An FOPDT model can be obtained by fitting the model to data. This allows other forms of step testing such as:

• Pulse: step up followed by step back to original value
• Doublet: two pulses in opposite directions
• Pseudo-Random Binary Sequence (PRBS): steps of varying frequency and magnitude
• Smart-stepping: optimize steps to extract the most information while keeping the process within bounds

In practice, smart-stepping or PRBS signals are used for identification of models for multivariable control. For tuning of PID controllers a step, doublet, or pulse test is often preferred.

• Lecture 6 Class Notes

Linear vs. Nonlinear Models

One example of comparing linear and nonlinear models is with the following gravity drained tank application.

Fig 1: Diagram of the Gravity Drained Tank

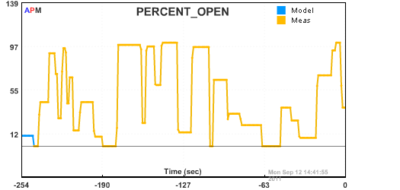
Fig 2: Sequence of Valve Movements to Test Models

Half of the class derived a FOPDT model of the process using empirical fitting techniques. The other half of the class used a material balance to obtain a model. A comparison of the two models is shown below:

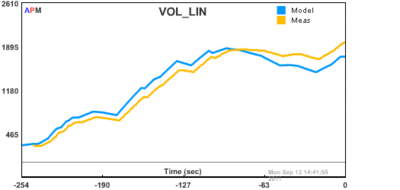
Fig 3: Linear Model (FOPDT). The linear response is easy to fit to the data but deviates, especially during the periods that are far from the steady state values.

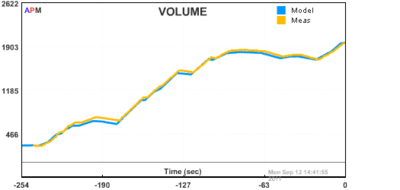
Fig 4: Nonlinear Model Based on a Material Balance. The nonlinear response is valid over a wider range of operation.

Discussion Questions

Test the lecture's ideas before or after class - commit to an answer first, then check it with a classmate or an AI tutor.

1. Two students fit the same step-test data. One reports K_p = 2, tau_p = 10 min; the other K_p = 4, tau_p = 10 min. What single steady-state calculation settles who is right, without refitting anything?
2. A linear FOPDT model fits the gravity-drained tank data beautifully near 50% valve opening but predicts nonsense near a full or empty tank. Why does the nonlinear balance model keep working where the empirical fit fails?
3. When would you choose a doublet or PRBS test over a simple step test, and what does the plant operator gain from that choice?
4. "The model fits the data, so it is correct." Give two ways a well-fitting model can still be wrong for control design.

App: Practice the fit on live data in the TCLab Simulation Studio - run a step test, fit K_p, tau_p, theta_p with sliders against a live objective function, and see how far the fitted model extrapolates before it breaks.