Simulation is a first step after the model development to verify convergence, validate the model response to input changes, and manually adjust parameters to fit an expected response. This section demonstrates how to set up and initialize a dynamic model simulation. Options such as CSV_READ control how much information is read from a data (CSV) file.
A first example shows how to use a scripting language such as MATLAB or Python to provide input values for a matrix of parameters.
import numpy as np
A = np.random.random((3,4))
n = np.size(A,0) # rows
m = np.size(A,1) # columns
# write model.apm
fid = open('model.apm','w')
fid.write('Constants \n')
fid.write(' n ='+str(n)+' \n')
fid.write(' m ='+str(m)+' \n')
fid.write(' \n')
fid.write('Parameters \n')
fid.write(' p[1:n][1::m] \n')
fid.write(' \n')
fid.write('Variables \n')
fid.write(' x \n')
fid.write('Equations \n')
fid.write(' x=p[1][1] \n')
fid.close()
# write data.csv
fid = open('data.csv','w')
for i in range(n):
for j in range(m):
fid.write(' p['+str(i+1)+']['+str(j+1)+'], '+str(A[i,j])+' \n')
fid.close()
# load model, data file, and solve
s = 'https://byu.apmonitor.com'
a = 'matrix_write'
apm(s,a,'clear all')
apm_load(s,a,'model.apm')
csv_load(s,a,'data.csv')
apm(s,a,'solve')
# retrieve solution
apm_web_var(s,a)
Although a problem may be written correctly, sometimes the solver fails to find a solution or requires excessive time to find a solution. Initialization strategies are critical in these situations to find a nearby solution that seeds the optimization problem with a starting point that allows convergence1.
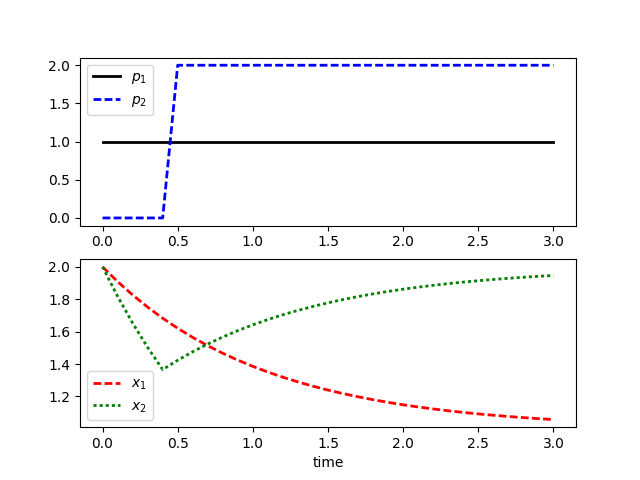
The following example is a demonstration of inserting different initial conditions or parameter values at points throughout the time horizon. A simulation solution is used to provide guess values for a subsequent simulation. The parameter CSV_READ can be set to 2 to provide the initial values for a calculated state. The default (CSV_READ=1) only updates the fixed values and skips the values that are calculated by the solver. Setting COLDSTART >= 1 also has the effect of using calculated values in the CSV file as initial guesses for the solver.
from APMonitor.apm import * # pip install APMonitor
##################################################################
## Step #1 - Solve model with p = 1
##################################################################
## Step #1a - write data.csv
n = 31
time = np.linspace(0,3,n)
p = np.ones(31)
x = 2 * np.ones(31)
fid = open('data.csv','w')
## write time row
fid.write('time, ')
for i in range(n-1):
fid.write(str(time[i]) + ', ')
fid.write(str(time[n-1]) + '\n')
## write 'p' row (input parameter)
fid.write('p, ')
for i in range(n-1):
fid.write(str(p[i]) + ', ')
fid.write(str(p[n-1]) + '\n')
## write 'x' row (state variable initialization)
fid.write('x, ')
# imode: https://apmonitor.com/wiki/index.php/Main/Modes
# for imode=4-6, include all initialization values
# for imode=7-9, include only the initial condition for variables
imode = 7
if ((imode>=4) and (imode<=6)):
for i in range(n-1):
fid.write(str(x[i]) + ', ')
fid.write(str(x[n-1]) + '\n')
else:
fid.write(str(x[0]) + ', ')
for i in range(1,n-1):
fid.write('-, ')
fid.write('-\n')
# close file
fid.close()
## Step 1b - Load and solve model
s = 'https://byu.apmonitor.com'
a = 'model_init'
apm(s,a,'clear all')
apm_load(s,a,'model.apm')
csv_load(s,a,'data.csv')
apm_option(s,a,'apm.time_shift',1)
apm_option(s,a,'apm.imode',imode)
output1 = apm(s,a,'solve')
## Step 1c - Retrieve results with solution.csv
solution1 = apm_sol(s,a)
##################################################################
## Step 2 - Solve again with prior solution for initialization and
## p as a step from 0 to 2
##################################################################
## Change to imode = 4 and change p trajectory
p[0:5] = 0.0
p[5:n] = 2.0
## Step 2a - Write new row at the end of solution.csv
fname = 'solution_' + a + '.csv'
fid = open(fname,'a') # append to file
fid.write('p, ')
for i in range(n-1):
fid.write(str(p[i]) + ', ')
fid.write(str(p[n-1]) + '\n')
# close file
fid.close()
## Step 2b - Reload csv file for initialization
apm(s,a,'clear csv')
csv_load(s,a,fname)
## Step 2c - Solve again but with new inputs
imode = 4
apm_option(s,a,'apm.time_shift',0)
apm_option(s,a,'apm.imode',imode)
output2 = apm(s,a,'solve')
print(output2)
## Step 2d - Retrieve results with solution.csv
solution2 = apm_sol(s,a)
##################################################################
## Step 3 - Create plots
##################################################################
import matplotlib.pyplot as plt
plt.figure(1)
plt.subplot(2,1,1)
plt.plot(solution1['time'],solution1['p'],'k-',lw=2)
plt.plot(solution2['time'],solution2['p'],'b--',lw=2)
plt.legend([r'$p_1$',r'$p_2$'])
plt.subplot(2,1,2)
plt.plot(solution1['time'],solution1['x'],'r--',lw=2)
plt.plot(solution2['time'],solution2['x'],'g:',lw=2)
plt.legend([r'$x_1$',r'$x_2$'])
plt.xlabel('time')
plt.show()
Exercise
Objective: Simulate a highly nonlinear system, using initialization strategies to find a suitable approximation for a future parameter estimation exercise. Create a MATLAB or Python script to simulate and display the results. Estimated Time: 2 hours
The spread of HIV in a patient is approximated with balance equations on (H)ealthy, (I)nfected, and (V)irus population counts2. Additional information on the HIV model is at the Process Dynamic and Control Course.
Initial Conditions H = healthy cells = 1,000,000 I = infected cells = 0 V = virus = 100 LV = log virus = 2 Equations dH/dt = kr1 - kr2 H - kr3 H V dI/dt = kr3 H V - kr4 I dV/dt = -kr3 H V - kr5 V + kr6 I LV = log10(V)
There are six parameters (kr1..6) in the model that provide the rates of cell death, infection spread, virus replication, and other processes that determine the spread of HIV in the body.
Parameters kr1 = new healthy cells kr2 = death rate of healthy cells kr3 = healthy cells converting to infected cells kr4 = death rate of infected cells kr5 = death rate of virus kr6 = production of virus by infected cells
The following data is provided from a virus count over the course of 15 years. Note that the virus count information is reported in log scale.
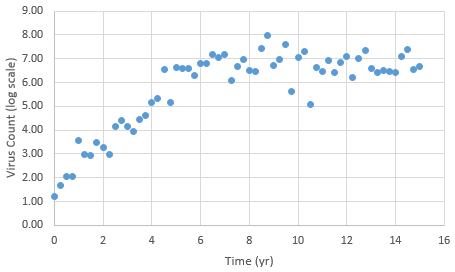
With guess values for parameters (kr1..6), approximately match the laboratory data for this patient. A subsequent section introduces methods for parameter estimation by minimizing an objective function.
Solution
import numpy as np
# Manually enter guesses for parameters
lkr = [3,np.log10(0.1),np.log10(2e-7),\
np.log10(0.5),np.log10(5),np.log10(100)]
# Model
m = GEKKO()
# Time
m.time = np.linspace(0,15,61)
# Parameters to estimate
lg10_kr = [m.FV(value=lkr[i]) for i in range(6)]
# Variables
kr = [m.Var() for i in range(6)]
H = m.Var(value=1e6)
I = m.Var(value=0)
V = m.Var(value=1e2)
# Variable to match with data
LV = m.CV(value=2)
# Equations
m.Equations([10**lg10_kr[i]==kr[i] for i in range(6)])
m.Equations([H.dt() == kr[0] - kr[1]*H - kr[2]*H*V,
I.dt() == kr[2]*H*V - kr[3]*I,
V.dt() == -kr[2]*H*V - kr[4]*V + kr[5]*I,
LV == m.log10(V)])
# option #1 for initialization
#m.options.IMODE = 7 # sequential simulation
# option #2 for initialization
m.options.IMODE = 4 #simultaneous simulation
m.options.COLDSTART = 2
m.options.SOLVER = 1
m.options.MAX_ITER = 1000
m.solve(disp=False)
# patient virus count data
data = np.array([[0,1.20E+00],[0.25,1.67E+00],[0.5,2.06E+00],\
[0.75,2.05E+00],[1,3.57E+00],[1.25,2.96E+00],\
[1.5,2.95E+00],[1.75,3.48E+00],[2,3.27E+00], \
[2.25,2.98E+00],[2.5,4.17E+00],[2.75,4.41E+00],\
[3,4.16E+00],[3.25,3.94E+00],[3.5,4.44E+00],\
[3.75,4.60E+00],[4,5.15E+00],[4.25,5.34E+00],\
[4.5,6.56E+00],[4.75,5.16E+00],[5,6.63E+00],\
[5.25,6.60E+00],[5.5,6.59E+00],[5.75,6.28E+00],\
[6,6.79E+00],[6.25,6.81E+00],[6.5,7.16E+00],\
[6.75,7.06E+00],[7,7.19E+00],[7.25,6.07E+00],\
[7.5,6.67E+00],[7.75,6.97E+00],[8,6.51E+00],\
[8.25,6.48E+00],[8.5,7.44E+00],[8.75,7.98E+00],\
[9,6.71E+00],[9.25,6.98E+00],[9.5,7.60E+00],\
[9.75,5.62E+00],[10,7.04E+00],[10.25,7.31E+00],\
[10.5,5.08E+00],[10.75,6.62E+00],[11,6.48E+00],\
[11.25,6.91E+00],[11.5,6.44E+00],[11.75,6.85E+00],\
[12,7.09E+00],[12.25,6.20E+00],[12.5,7.02E+00],\
[12.75,7.34E+00],[13,6.57E+00],[13.25,6.42E+00],\
[13.5,6.50E+00],[13.75,6.46E+00],[14,6.42E+00],\
[14.25,7.09E+00],[14.5,7.37E+00],[14.75,6.56E+00],\
[15,6.69E+00]])
# Convert log-scaled data for plotting
log_v = data[:,1] # 2nd column of data
v = np.power(10,log_v)
# Plot results
import matplotlib.pyplot as plt
plt.figure(1)
plt.semilogy(m.time,H,'b-')
plt.semilogy(m.time,I,'g:')
plt.semilogy(m.time,V,'r--')
plt.semilogy(data[:,][:,0],v,'ro')
plt.xlabel('Time (yr)')
plt.ylabel('States (log scale)')
plt.legend(['H','I','V'])
plt.show()
References
- Safdarnejad, S.M., Hedengren, J.D., Lewis, N.R., Haseltine, E., Initialization Strategies for Optimization of Dynamic Systems, Computers and Chemical Engineering, 2015, Vol. 78, pp. 39-50, DOI: 10.1016/j.compchemeng.2015.04.016. Article
- Nowak, M. and May, R. M. Virus dynamics: mathematical principles of immunology and virology: mathematical principles of immunology and virology. Oxford university press, 2000.
- Lewis, N.R., Hedengren, J.D., Haseltine, E.L., Hybrid Dynamic Optimization Methods for Systems Biology with Efficient Sensitivities, Special Issue on Algorithms and Applications in Dynamic Optimization, Processes, 2015, 3(3), 701-729; doi:10.3390/pr3030701. Article
